- #176
unusualname
- 664
- 3
but I should add, that at least Ken G makes arguments which are understandable and (thus) debateable, unlike Goldstone1 above^^
Actually, nothing in this thread has anything to do with my understanding of QM, which is actually just fine thank you. This thread is all about classical analogs of QM, which has to do with other approaches to understanding similar concepts (like diffraction). I'm not even sure you quite understand how physics works in the first place, so let's start at the beginning.unusualname said:I just want to withdraw a statement I made above that Ken G has a good understanding of QM. I read a few discussions that were on an elementary level which misled me.
Ken G said:Then you didn't look at those papers I cited? There's a whole field of study called "scalar diffraction theory", it's all perfectly classical. Oh and yes, it has been applied to neutrons and electron diffraction, it's just that many times the quantum mechanics is all you need, and is more generally applicable. That's what I mean by the "accident of history"-- had neutron and electron diffraction been known about in 1880, instead of the 1930s, it would have been more important.
Actually, you have never once gave a single reason why you think only the diffraction of massless particles is classically describable, but that the diffraction of neutrons has no classical analog. Would you like to take that opportunity right now? Because I have no idea why you think that.
Excellent, then you actually agree with my central thesis all along (would you like to count the number of times I used the word "analog" in this thread?). I'm glad to discover this, I can then disregard all your objections to it because you apparently agree with it.
Many things get called the correspondence principle. I've been painstakingly clear about the meaning I've taken. I'm glad to find that if you just take my meaning, you agree with me.
Let's apply your exact argument to photons. You're saying that if each photon has a lot of energy, then they won't diffract. No kidding!
The correspondence principle applied to bright radiation fields is a theory that describes the diffraction of classical concepts like the Poynting flux.
Which, by the way, has nothing at all to do with the energy per photon, as I"ve told you about a hundred times.
Well, as I've repeated many times by now, supporting things you said doesn't make any difference at all, because the vast majority of them had nothing whatsoever to do with what I said. For example, you've mentioned many times that high-energy particles don't show wave effects, which is perfectly obvious and I may have known that since longer than you've been alive for all I know, so is just another example of all the things you can claim "support" for that are totally irrelevant to anything I said.SpectraCat said:That is just a bunch of sophistry, obfuscation, and general gobbledy-gook. I doubt you have any idea what scalar diffraction theory is, and I doubt you read those papers you linked. I couldn't access the second one, but the first one provides strong support for the point of view I have expressed on this thread.
Ken G said:Well, as I've repeated many times by now, supporting things you said doesn't make any difference at all, because the vast majority of them had nothing whatsoever to do with what I said.
Let's cut right to the heart of this. We all know that diffraction is a phenomenon that connects with interference, so it connects with a concept of phase and periodicity and propagation, so it connects with a concept of wavelength. That's just the nature of the phenomenon, whether classical or quantum mechanical or string theoretical.
... there is nothing fundamentally quantum mechanical about the concept of either wavelength, or phase, or interference, or diffraction--
of a photon or a neutron or anything else. The only thing that makes it quantum mechanical is that for some set of questions we wish to know about, we need to use quantum mechanics.
An excellent example of what I am talking about is Bragg scattering. Discovered and explained with classical diffraction theory in 1913, it led to a Nobel prize. It was later found that Bragg's law also applied to neutrons and electrons, but by then we already had quantum mechanics. We also had the photoelectric effect well before Bragg, but Bragg didn't need it, he used a classical model anyway, even though it was known that photons were particles. "So what if photons are particles", he might have said, "I'm just using a classical theory to understand how light can probe crystals." Maxwell's equations didn't disappear when Shroedinger came around.
Now, from the above, we can conclude you are thinking "he's confusing photons with neutrons". No, I'm not, you just don't understand what I'm saying. Electron diffraction was discovered in 1927, neutron diffraction shortly afterward. To understand what I'm saying, you need to imagine that the photoelectric effect had not yet been discovered, nor Planck's law, nor any of quantum mechanics, yet we have Bragg scattering of X-rays in 1913, and electron diffraction in crystals. How would the edifice of physics handle this situation? Throw up its hands because it doesn't have quantum mechanics? No, absolutely not-- Bragg's law, a classical law, simply gets applied to neutrons and electrons, because it is seen to help understand diffraction in crystals!
So now you are ready for what I've actually been saying all this time. Even if the accidents of history are such that we already have quantum mechanics when electron diffraction is found (and indeed anticipated), we can still benefit from that same classical analogy that we would have been forced to use had electron diffraction been discovered before quantum mechanics! All it says is we would recognize that the classical concept of wavelength was relevant to diffraction of an electron beam, and that would be true whether we knew the beam had particles in it, or even if we didn't know that.
The rest of your post is an ode to misunderstanding this point, so constitutes a bunch of physical facts I've known for a long time and have no bearing on this issue at all.
Once again, you have gone off into left field, telling me perfectly obvious things that have nothing to do with what I said. I'm not saying you are stupid, you obviously aren't. There is just something blocking you from actually hearing what I'm saying, so you keep telling me things that any first-year student knows. It's irrelevant, what I'm saying is that Bragg did not need to know that light was quanta to get Bragg scattering, and he wouldn't have needed to know that electrons or neutrons were quanta to extend his classical insights to electron and neutron diffraction. He might not have obtained quantum mechanics, but he would have gotten insights into it-- classically. Or maybe he would have gotten quantum mechanics, using those insights, just as Schroedinger himself did.SpectraCat said:Whoops, not fine anymore .. strictly speaking there is no classical physics context in which it makes sense to talk about particles like photons, electrons and neutrons *at all*, let alone the fact that massive bodies have wavelengths associated with them.
Of course there is, you just put it into a classical wave theory. You might not even know you are dealing with massive bodies, and do the classical physics anyway-- that was the point of that student experiment I mentioned. Physics has lots of different theories, and we will have a lot more. We might get a working string theory, we might unify gravity and quantum physics, we might understand what intelligence is, who knows. They'll all look a lot different from the previous theories, but the clever physicist will always look for the analogs from the previous theories, like classical analogs-- that's the correspondence principle. Read the whole thread again, realizing that this is what I have been saying, and recognizing that I know quantum mechanics, and I know classical mechanics, and I see the value of classical analogs-- and you can too.Classical laws of physics treat space, time and matter as infinitely divisible, and as such there is no way in classical physics for massive bodies to have wave-like properties.
There's that language again, that's just baloney. In Newton's day, did they say "acceleration is a strictly Newtonian concept" simply because they had F=ma and no one else had a theory to make sense of dynamics? Would we say today that acceleration is strictly Newtonian? Physical theories are just that-- theories. They never own the phenomena they describe-- never. There is no such thing as any phenomenon that is "strictly classical", or "strictly quantum", there are just concepts, and the concepts have analogs very often, and it's useful to know those analogs, because they help you understand the concepts, and they help you form the new theories. As they did for Bragg, as they did for Schroedinger, as they certainly did for Bohr.Once you are talking about space (or phase space) as having a fundamental limit of divisibility, or about matter as consisting of discrete subatomic particles with associated wavelengths, then the concepts you are invoking are strictly quantum mechanical.
Whoops? Are you kidding? Are you aware that Maxwell's equations are classical laws? Bragg's law is a consequence of Maxwell's equations applied to a regular lattice interacting with a classical E&M field. If your argument rests on the idea that Bragg's law was not obtained via classical reasoning, I think that sums up the quality of your argument.Whoops! What makes Bragg's law a *classical* law? Absolutely nothing
Ah, so now we see that your argument rests solely on a tautology: you simply define electrons as quantum systems, so any law that electrons obey is automatically a quantum law, so there can be no correspondence to electron diffraction because electrons are doing it. Well, I can't argue against a tautology, but I can sure question its information content... it is a *physical* law describing wave phenomena that was simply first discovered in a classical context. It describes classical phenomena when applied to classical systems, and quantum phenomena when applied to quantum systems.
Which is exactly what I have been telling you all along. Nothing that you are talking about has anything to do with the point I raised, and clearly described, and told you that your comments were irrelevant to it, yet still somehow you thought you were proving me wrong.It may have great relevance in terms of Ken's correspondence principle of analogies, but that is not what I have been talking about ... ever.
Obviously, and again because of a semantic tautology: the HUP is a classical analog of how classical waves behave, applied, to our surprise, to particles-- but since it applies to particles, you get to label it a "quantum law"! And in so labeling, you miss my entire point: the HUP is a perfect example of the value of a classical analogy, the Fourier analysis of classical waves. As I said about a zillion posts ago.On the other hand, Heisenberg's Uncertainty Principle is a *quantum law* of physics, in that it applies exclusively to the phenomena of quantum systems.
Yes, again tautologically true, because you think what matters is the quantum label, not noticing that what actually matters about the de Broglie wavelength is the classical analog. That's why it is called a "wavelength" in the first place, it's invoking a classical analog that is of great value in understanding it. And like I said above, it does relate to a classical treatment in the limit of a huge ensemble of particles all with that deBroglie wavelength-- just as it did for Bragg's derivation of Bragg's law.The de Broglie wavelength is also a purely quantum concept.
Well this is progress-- you now see that those "strictly QM" concepts benefit from classical analogs! That's what I've been saying, by the way-- just read the thread. Obviously they don't apply to classical physics in your mind, because you simply haven't yet taken the classical limit of lots and lots of particles, in which case they do apply to classical wave mechanics, which is why Bragg's law is useful for diffraction of beams of electrons and neutrons. That was the whole point of that "student experiment" I explained that I thought would make this all immediately clear.Both the HUP and the de Broglie wavelength may be ANALOGOUS to concepts found in classical physics, but the specific concepts don't themselves apply to classical physics.
Diffraction is undetectable in the classical limit? Then we must revoke the Bragg's Nobel prize, that's a pity. (Oh yes, once again you will think I mean the classical limit of large particle energies, though we all know that would eliminate the diffraction and I have said so many times I know that and I am talking about the limit that Bragg was actually involved in-- the limit of large particle fluxes, such that indeed there was no need to know there were even particles there to get Bragg's results. Read that again if needed.)Finally, since these are purely quantum concepts, the phenomena they predict (such as diffraction of massive bodies) must be "averaged out" in such a away that they are undetectable in the classical limit .. that is what is required by Bohr's principle of quantum-classical correspondence.
No, the reason you think it works for photons but not electrons is simply that a high quantum number for a photon field is the same as a high occupation number, so we have just one classical limit instead of two separate ones. I made perfectly clear which classical limit I'm talking about, whether photons or electrons-- the limit of large enough fluxes that you can measure them as classical energy fluxes, and use a classical wave theory to interpret that as Poynting flux. I don't know how many times I need to say that this is the classical limit I have been referring to in regard to the correspondence principle for both electrons and photons, just look back at that "student experiment" post again, if you can find it in all the misconstruals I've had to suffer.Note that there is no such requirement that diffraction of massless photons be "averaged out" in the same fashion, because photons are just a way of counting up the population of the harmonic modes of the underlying field, which ends up having the same basic description in both (quantum) QED and (classical) E&M.
I'm not sure why you would make such a false statement, that "the quantum character of photons has nothing to do with the wavelength of the field." I'm going to presume you had a momentary lapse and let that go, no doubt you will immediately see your error.So the quantum character of photons has nothing to do with the wavelength of the field, but only it's intensity, which means that the wave-like character persists even in the classical limit.
I tried very hard to tell you that your objections were not relevant to what I was saying. I thought I was being pretty clear-- the problem is that you still don't recognize a classical limit of high phase-space density, even after I explained exactly how purely classical experiments can be done on such systems, and how one can generally avoid invoking particle concepts, as is done in hydrodynamics, wave mechanics, and continuum mechanics of all kinds. I said all that, many times. Which finally brings us back to the OP-- the correspondence principle I was talking about, right from the very start, was about interpreting Bohmian trajectories in terms of large ensemble averages of weak measurements, and I claimed, and still do, that was tantamount to taking exactly the kind of "averaging out" classical-wave limit that we are just now talking about. That was the motivation right from the start.If you had said what you wrote in the quoted paragraph above in the first place, then I never would have disagreed with you.
No. There is not one single incorrect claim I made that isn't basically a technicality, like issues with quantum chaos. In every case, your "corrections" were telling me basic physics I've known for decades. Every time, you told me nothing I didn't already know, and it was always just plain irrelevant to the correspondence principle applied to ensemble averages of weak measurements.But you didn't say that, you made incorrect claims about physics, which I corrected.
We certainly see that Bragg's approach is purely classical and can be applied to electron diffraction. So that's a pretty good start. Whether we wish to count that as a "theory" is less clear, you may want more from it than just its ability to probe the structure of a lattice. There are many types of diffraction theories, and they all work to various degrees in different situations-- such is the nature of physics, we make idealizations to get somewhere. So we would not ask a classical theory of electron diffraction to do more than help us understand what is going on when we have large ensembles of diffracting electrons, and that's what Bragg's approach, and scalar diffraction theory in general, can do for us. It's just that we have quantum mechanics, so we only use classical concepts as analogs to help us understand the quantum mechanics, that is often the main point of classical analogs. Bragg's law is a perfect example of a classical analog helping us understand how electrons and neutrons diffract in a crystal.You refused to accept my corrections for a while, but if you now accept that I was right all along, and that you were wrong to claim (among other things, but this is the biggie) that it is possible to formulate a classical theory that can predict electron diffraction (which you did in post #113, and several times thereafter), then fantastic!
Excellent, then we are actually in a position to get the whole point here: classical analogs are a useful way to understand phenomena that closedminded people tend to brand as "strictly quantum." And that was the whole point, in particular about using Poynting fluxes to understand streamline diagrams like the one in the OP.If you want to use your fuzzy philosophical definition of the correspondence principle that is based in analogies, then fine .. feel free.
Bohr's correspondence principle is itself a fuzzy philosophical rule, and it is the reason that physics is successful, in a nutshell. I'm sure Bohr understood that, but the point seems to have been rather lost to the years.Just be clear about it and don't confuse others by pretending that it is equivalent to the physical correspondence principle laid out by Bohr to help relate and distinguish quantum and classical theories.
Correction, your interpretation of them made you believe that. It's just not true. For fear of making you think you completely wasted your time telling me things I already knew, the course of the discussion has helped me hone some of the stickier issues, and certainly has helped me see the areas that are most easily misconstrued. Really the only thing I said that I have not backed up is the extent to which quantum theories can be used to generate classical ones-- that remains a bit vague, though I think it's mostly that there just isn't much payoff for doing it when all one really wants is the classical analog concepts (and there is a nice payoff for those, like the Lorentz wings of a resonance line, like the Thomson cross section, like the concept of a "classical radius of the electron", the list just goes on and on). My real point is to look for classical analogs, which in the case of Bohmian trajectories may well just be Poynting flux streamlines.You may have "known" the facts I have used to explain my arguments, but your posts make it quite obvious that you have never understood many of them in the proper context.
Ken G said:Once again, you have gone off into left field, telling me perfectly obvious things that have nothing to do with what I said. I'm not saying you are stupid, you obviously aren't. There is just something blocking you from actually hearing what I'm saying, so you keep telling me things that any first-year student knows. It's irrelevant, what I'm saying is that Bragg did not need to know that light was quanta to get Bragg scattering, and he wouldn't have needed to know that electrons or neutrons were quanta to extend his classical insights to electron and neutron diffraction. He might not have obtained quantum mechanics, but he would have gotten insights into it-- classically. Or maybe he would have gotten quantum mechanics, using those insights, just as Schroedinger himself did.
I just don't know how else to get this across to you. Only after it was discovered that electrons and neutrons were particles, had the Braggs not known that (or just choosed not to use it, like they didn't use the knowledge with photons), could someone have taken adantage of the classical-wave analog to say "hey, we must have wave/particle duality here." Indeed, wave/particle duality itself, the cornerstone of what is "strictly quantum", is a perfect example of the value of classical analogs. So although you have gone on and on about wave/particle duality of electrons and how there can't be any useful classical analog there, the ultimate irony is: that is a classical analog, in that very language. Yes, it is, we are invoking a classical analog to understand quantum behavior, as is so extremely common in all of physics (consider the examples I gave above in that addendum to my last post, you might have missed it).
Of course there is, you just put it into a classical wave theory. You might not even know you are dealing with massive bodies, and do the classical physics anyway-- that was the point of that student experiment I mentioned. Physics has lots of different theories, and we will have a lot more. We might get a working string theory, we might unify gravity and quantum physics, we might understand what intelligence is, who knows. They'll all look a lot different from the previous theories, but the clever physicist will always look for the analogs from the previous theories, like classical analogs-- that's the correspondence principle. Read the whole thread again, realizing that this is what I have been saying, and recognizing that I know quantum mechanics, and I know classical mechanics, and I see the value of classical analogs-- and you can too.
There's that language again, that's just baloney. In Newton's day, did they say "acceleration is a strictly Newtonian concept" simply because they had F=ma and no one else had a theory to make sense of dynamics? Would we say today that acceleration is strictly Newtonian? Physical theories are just that-- theories. They never own the phenomena they describe-- never. There is no such thing as any phenomenon that is "strictly classical", or "strictly quantum", there are just concepts, and the concepts have analogs very often, and it's useful to know those analogs, because they help you understand the concepts, and they help you form the new theories. As they did for Bragg, as they did for Schroedinger, as they certainly did for Bohr.
Whoops? Are you kidding? Are you aware that Maxwell's equations are classical laws? Bragg's law is a consequence of Maxwell's equations applied to a regular lattice interacting with a classical E&M field. If your argument rests on the idea that Bragg's law was not obtained via classical reasoning, I think that sums up the quality of your argument.
Ah, so now we see that your argument rests solely on a tautology: you simply define electrons as quantum systems, so any law that electrons obey is automatically a quantum law, so there can be no correspondence to electron diffraction because electrons are doing it. Well, I can't argue against a tautology, but I can sure question its information content.
Which is exactly what I have been telling you all along. Nothing that you are talking about has anything to do with the point I raised, and clearly described, and told you that your comments were irrelevant to it, yet still somehow you thought you were proving me wrong.
Obviously, and again because of a semantic tautology: the HUP is a classical analog of how classical waves behave, applied, to our surprise, to particles-- but since it applies to particles, you get to label it a "quantum law"! And in so labeling, you miss my entire point: the HUP is a perfect example of the value of a classical analogy, the Fourier analysis of classical waves. As I said about a zillion posts ago.
Yes, again tautologically true, because you think what matters is the quantum label, not noticing that what actually matters about the de Broglie wavelength is the classical analog. That's why it is called a "wavelength" in the first place, it's invoking a classical analog that is of great value in understanding it. And like I said above, it does relate to a classical treatment in the limit of a huge ensemble of particles all with that deBroglie wavelength-- just as it did for Bragg's derivation of Bragg's law.
Well this is progress-- you now see that those "strictly QM" concepts benefit from classical analogs! That's what I've been saying, by the way-- just read the thread. Obviously they don't apply to classical physics in your mind, because you simply haven't yet taken the classical limit of lots and lots of particles, in which case they do apply to classical wave mechanics, which is why Bragg's law is useful for diffraction of beams of electrons and neutrons. That was the whole point of that "student experiment" I explained that I thought would make this all immediately clear.
Diffraction is undetectable in the classical limit? Then we must revoke the Bragg's Nobel prize, that's a pity. (Oh yes, once again you will think I mean the classical limit of large particle energies, though we all know that would eliminate the diffraction and I have said so many times I know that and I am talking about the limit that Bragg was actually involved in-- the limit of large particle fluxes, such that indeed there was no need to know there were even particles there to get Bragg's results. Read that again if needed.)
No, the reason you think it works for photons but not electrons is simply that a high quantum number for a photon field is the same as a high occupation number, so we have just one classical limit instead of two separate ones. I made perfectly clear which classical limit I'm talking about, whether photons or electrons-- the limit of large enough fluxes that you can measure them as classical energy fluxes, and use a classical wave theory to interpret that as Poynting flux. I don't know how many times I need to say that this is the classical limit I have been referring to in regard to the correspondence principle for both electrons and photons, just look back at that "student experiment" post again, if you can find it in all the misconstruals I've had to suffer.
I'm not sure why you would make such a false statement, that "the quantum character of photons has nothing to do with the wavelength of the field." I'm going to presume you had a momentary lapse and let that go, no doubt you will immediately see your error.
I tried very hard to tell you that your objections were not relevant to what I was saying. I thought I was being pretty clear-- the problem is that you still don't recognize a classical limit of high phase-space density, even after I explained exactly how purely classical experiments can be done on such systems, and how one can generally avoid invoking particle concepts, as is done in hydrodynamics, wave mechanics, and continuum mechanics of all kinds. I said all that, many times. Which finally brings us back to the OP-- the correspondence principle I was talking about, right from the very start, was about interpreting Bohmian trajectories in terms of large ensemble averages of weak measurements, and I claimed, and still do, that was tantamount to taking exactly the kind of "averaging out" classical-wave limit that we are just now talking about. That was the motivation right from the start.
No. There is not one single incorrect claim I made that isn't basically a technicality, like issues with quantum chaos. In every case, your "corrections" were telling me basic physics I've known for decades. Every time, you told me nothing I didn't already know, and it was always just plain irrelevant to the correspondence principle applied to ensemble averages of weak measurements.
We certainly see that Bragg's approach is purely classical and can be applied to electron diffraction. So that's a pretty good start. Whether we wish to count that as a "theory" is less clear, you may want more from it than just its ability to probe the structure of a lattice. There are many types of diffraction theories, and they all work to various degrees in different situations-- such is the nature of physics, we make idealizations to get somewhere. So we would not ask a classical theory of electron diffraction to do more than help us understand what is going on when we have large ensembles of diffracting electrons, and that's what Bragg's approach, and scalar diffraction theory in general, can do for us. It's just that we have quantum mechanics, so we only use classical concepts as analogs to help us understand the quantum mechanics, that is often the main point of classical analogs. Bragg's law is a perfect example of a classical analog helping us understand how electrons and neutrons diffract in a crystal.Excellent, then we are actually in a position to get the whole point here: classical analogs are a useful way to understand phenomena that closedminded people tend to brand as "strictly quantum." And that was the whole point, in particular about using Poynting fluxes to understand streamline diagrams like the one in the OP.
Bohr's correspondence principle is itself a fuzzy philosophical rule, and it is the reason that physics is successful, in a nutshell. I'm sure Bohr understood that, but the point seems to have been rather lost to the years.
Correction, your interpretation of them made you believe that. It's just not true. For fear of making you think you completely wasted your time telling me things I already knew, the course of the discussion has helped me hone some of the stickier issues, and certainly has helped me see the areas that are most easily misconstrued. Really the only thing I said that I have not backed up is the extent to which quantum theories can be used to generate classical ones-- that remains a bit vague, though I think it's mostly that there just isn't much payoff for doing it when all one really wants is the classical analog concepts (and there is a nice payoff for those, like the Lorentz wings of a resonance line, like the Thomson cross section, like the concept of a "classical radius of the electron", the list just goes on and on). My real point is to look for classical analogs, which in the case of Bohmian trajectories may well just be Poynting flux streamlines.
No, that is what you imagined happened. What actually happened is what I just said to zenith8-- I pointed out that the people who were claiming that averaging lots of weak measurements could demonstrate that photons going through the left slit had to hit the left wall were making a preposterous argument, which can be understood by simply understanding the information that gets lost when one takes a classical limit over a large ensemble. Then a few people who seemed unable to grasp that very clear truth went off on it. My main mistake was in imagining that people understood the classical analogs of wave diffraction and Poynting fluxes, and why the correspondence principle assures that those notions are going to be relevant when you do an ensemble average over individual quantum measurements. This is also why Bragg's law, discovered for X-rays, would have also been tried as an application to electron and neutron diffraction, even if the Braggs had not known that electrons and neutrons were particles, and even if there had been no quantum mechanics. It's simply the way physics is done-- we find concepts and look for places to apply them, and classical limits admit to classical analysis-- just like the "average trajectories" in the two-slit experiment. Analysis doesn't mean you can answer all the questions, it means you have made useful discoveries and gained useful insights, using classical approaches like Maxwell's equations and Huygen's principle. I wonder if you even understand this now.SpectraCat said:So basically, what happened is that you came on a physics website, and started posting unsubstantiated claims based on your personal definitions and interpretations of well-established physical concepts, like the distinction between quantum and classical, the distinction between occupation numbers and quantum numbers, and Bohr's principle of quantum classical correspondence.
Ken G said:Actually, nothing in this thread has anything to do with my understanding of QM, which is actually just fine thank you. This thread is all about classical analogs of QM, which has to do with other approaches to understanding similar concepts (like diffraction). I'm not even sure you quite understand how physics works in the first place, so let's start at the beginning.
In physics, we do observations, see phenomena that seem strange-- whether it be acceleration, diffraction, or entanglement. We then design theories to help us understand and predict. At what point do those theories take ownership of the observed phenomena, such that we could correctly say that phenomena is "strictly classical" or "strictly quantum mechanical" or "strictly field theoretic?" Never. At no time do those claims make any sense at all, because the phenomena are just phenomena, owned by themselves, not by any theory. Yes, theories can explain them to some degree, but all theories have their domains of applicability, like classical physics, like quantum mechanics. Eventually, a new theory comes along that is more fundamental, and everything that used to be "strictly classical" or "strictly quantum mechanical" is now not so strictly those things, because they never actually were in the first place.
This is the point of the correspondence principle, to understand the connections between these different theories and the observations they help understand, and why a phrase like "diffraction of particles that have mass is strictly quantum mechanical" is really just a mistake about how physics works. That you see it in many places is just because people get a bit lazy about it, but when you look at the endeavor of physics from a safe height, it's obvious what I'm saying here is true. Forest for the trees, I'm afraid.
zenith8 said:Slightly off topic.. can anyone point me to a thread on Physics Forums where any contributor with more than - say - 10 posts changes their mind about anything, ever? Just curious.
Ken G said:Blah.. Blah.. Blah.. Blah.. Blah.. Blah blah blah blah blah.. Blah.
The correspondence principle goes way past Bohr and classical/quantum. It is the reason we can do physics, even though we don't get the fundamental theory out of the blocks, we have to muddle along with better and better theories that nevertheless work quite well in their domains of application. That's all Bohr was saying, I think his point there was pretty obvious and will be just as true for quantum/string as it was for classical/quantum.unusualname said:Yes but as I've explained the correspondence principle was just a wishy-washy prelude to the much more specific Decoherence argument, which your hero Bohr never managed to quite formulate.
Useful aids to thinking are rare and valuable-- and never out-dated.The correspondence principle is just an out-dated, though sometimes useful, aid to thinking.
Yes, more fundamental theories can always describe the less fundamental ones, plus more.{EDIT} But the physicist tailors the theory used to the depth of the question at hand, not to the most fundamental theory available. That's why Newton's gravity still gets used far more often than Einstein's{EDIT}. So that's why the issue here is, we should not fool ourselves into thinking we are making a quantum-mechanical argument when we do so much averaging of the quantum data that we end up with nothing but the classical limit.The only thing decoherence doesn't solve is the "measurement problem", it otherwise explains the macroscopic world "strictly quantum mechanically" as you say.
Then I guess you'll just miss the point of the thread. No problem for me there.zenith8 said:Not the answer I was looking for, Kenny..
http://en.wikipedia.org/wiki/Quantum_mechanics#Quantum_mechanics_and_classical_physics
Quantum mechanics and classical physics
Predictions of quantum mechanics have been verified experimentally to a extremely high degree of accuracy. According to the correspondence principle between classical and quantum mechanics, all objects obey the laws of quantum mechanics, and classical mechanics is just an approximation for large systems (or a statistical quantum mechanics of a large collection of particles). The laws of classical mechanics thus follow from the laws of quantum mechanics as a statistical average at the limit of large systems or large quantum numbers.
Quantum coherence is an essential difference between classical and quantum theories, and is illustrated by the Einstein-Podolsky-Rosen paradox. Quantum interference involves adding together probability amplitudes, whereas when classical waves interfere there is an adding together of intensities. For microscopic bodies, the extension of the system is much smaller than the coherence length, which gives rise to long-range entanglement and other nonlocal phenomena characteristic of quantum systems. Quantum coherence is not typically evident at macroscopic scales, although an exception to this rule can occur at extremely low temperatures, when quantum behavior can manifest itself on more macroscopic scales (see Bose-Einstein condensate and Quantum machine).
http://en.wikipedia.org/wiki/Quantum_machine
The first Quantum Machine
The first quantum machine was created on August 4, 2009 by Aaron D. O'Connell while pursuing his Ph.D. under the direction of Andrew N. Cleland and John M. Martinis at the University of California, Santa Barbara. O'Connell and his colleagues coupled together a mechanical resonator, similar to a tiny springboard, and a qubit, a device that can be in a superposition of two quantum states at the same time. They were able to make the resonator vibrate a small amount and a large amount simultaneously — an effect which would be impossible in classical physics. The mechanical resonator was just large enough to see with the naked eye — about as long as the width of a human hair. The groundbreaking work was subsequently published in the journal Nature in March 2010. The journal Science declared the creation of the first quantum machine to be the "Breakthrough of the Year" of 2010.

Photograph of the quantum machine developed by O'Connell. The mechanical resonator is located to the lower left of the coupling capacitor (small white square). The qubit is connected to upper right of the coupling capacitor.
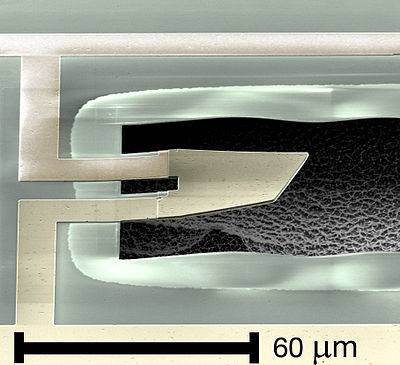
Scanning electron micrograph of the film bulk acoustic resonator. The mechanically active part of the resonator is supported to the left by two metal leads which act as electrical connections.
^^ Ken g said:But I should correct one factual error-- I never claimed, nor thought, that the correspondence principle was a "law of nature." In fact, I don't believe there is any such thing as a law of nature. But there are quite a few "laws" that physicists have found great use from, and what we choose to call a law is a pretty irrelevant exercise in scientific sociology. But feel free to decide what you personally do and do not consider to be a law of nature, just don't expect anyone else to care.
unusualname about 3 pages back said:The correspondence principle is not a law of nature, it simply a rule for us dumb humans to check that our (quantum mechanical) model of reality is consistent.
Ken G, struggling with the logic reallyKen G (in reply) said:I'm afraid that's a pretty good definition of a "law of nature." Why you see a distinction there is certainly outside anything that could be called science.
Ken G said:But I should correct one factual error-- I never claimed, nor thought, that the correspondence principle was a "law of nature." In fact, I don't believe there is any such thing as a law of nature.
unusualname said:The correspondence principle is not a law of nature, it's simply a rule for us dumb humans to check that our (quantum mechanical) model of reality is consistent.
Ken G said:I'm afraid that's a pretty good definition of a "law of nature."
Ken G said:But there are quite a few "laws" that physicists have found great use from, and what we choose to call a law is a pretty irrelevant exercise in scientific sociology.

Ken G said:What actually matters is what we use, and how it helps us, and we certainly use the correspondence principle, writ large, constantly in physics. I described what I meant by that principle-- that more fundamental theories that apply in wider domains of application must still be consistent with less fundamental theories in the domain of demonstrable success of the latter.
Ken G said:I don't know how many times I need to say that this is the classical limit I have been referring to in regard to the correspondence principle for both electrons and photons, just look back at that "student experiment" post again, if you can find it in all the misconstruals I've had to suffer.
Sorry, but you once again failed to make your point. I did not claim it was a law of nature, I claimed that you were making an arbitrary distinction between what is and is not a "law of nature." As I just said, I personally don't think "law of nature" applies to anything that physics does, but it may apply to lots of things physics does, including the correspondence principle, using someone else's meaning of the phrase. My actual point was that your attempt to deny the value of the correspondence principle on the grounds that it was "not a law of nature" was ridiculous. Which it was. I might as well say Newton's laws are not laws of nature either, which they aren't-- but it would be an equally meaningless argument. We don't do physics by labeling things.unusualname said:Ken G, struggling with the logic really
See above. You failed to understand my point once again,which was that the whole "law of nature" hooey, not even brought up by me, was a complete red herring, because the term is completely nonspecific and can be applied to the correspondence principle or not applied to it, depending on how one defines it. I also pointed out that the important attributes of the correspondence principle could easily be construed as that, unless someone wanted to offer a more specific definition. Which they did not, of course. Pray tell, do you know what a law of nature is? Be sure to include references, of course, I'm sure the textbooks will be quite informative on the topic. Oh and, it would be nice if that completely arbitrary list that you seem to think are laws of nature would actually conform to the definition you dig up, but the correspondence principle does not. And it doesn't even matter if you can shoehorn a definition into that space, because my argument did not rest on what we call things, it rested on what is necessary for the endeavor of physics to actually work.DevilsAvocado said:I’m afraid you’re making a fool of yourself again. You apparently missed the "First law of internet":
Never deny a statement of yours that’s only a few posts away and that can never be erased.
That the principle has many sides does not make them incompatible. Is your face incompatible with your posterior? Is it different?I hope you understand the contradiction in advocating two different and completely incompatible versions of the correspondence principle? One is old and obsolete (classical limit), and the other (backward compatibility) is rejected by Niels Bohr, since he argued that classical physics does not emerge from quantum physics in the same way that classical mechanics emerges as an approximation of special relativity at small velocities.
Ken G said:Sorry, but you once again failed to make your point. I did not claim it was a law of nature, I claimed that you were making an arbitrary distinction between what is and is not a "law of nature." As I just said, I personally don't think "law of nature" applies to anything that physics does, but it may apply to lots of things physics does, including the correspondence principle, using someone else's meaning of the phrase. My actual point was that your attempt to deny the value of the correspondence principle on the grounds that it was "not a law of nature" was ridiculous. Which it was. I might as well say Newton's laws are not laws of nature either, which they aren't-- but it would be an equally meaningless argument. We don't do physics by labeling things.
So your argument is that when we have a more sophisticated understanding of something, the more basic principles disappear? We have a more sophisticated understanding of gravity, but Newton's gravity has not disappeared from scientific journals. We have a more sophisticated understanding of the statistical mechanics of van der Waals forces, but the ideal gas law has not disappeared. We have a more sophisticated understanding of quantum mechanics, but classical mechanics has not disappeared. This is all the beating heart of the correspondence principle, writ large-- science is an endeavor that routinely matches the complexity of the description to the domain of interest of the outcome. None of that has disappeared, no.unusualname said:A law of nature is something we humans conceive to be the way nature works .The correspondence principle is a now not very important philosophical principle, since we have a much more sophisticated understanding of how the macroscopic emerges from the microscopic.
Completely wrong. That is not at all what I said, thought, or advocated in any way. As I've told you over and over, that is some make believe version of what I said, that you invented so you could attack it. I frankly have no idea where you got that from. Oh, and I pointed this out prior to your reference, so the point was not "thanks to" your reference, it was merely supported by your reference. A fact which seems to have escaped you here, but thank you.Your argument on this thread amounts to this - the flux lines for single photons can be (qualitatively) classically constructed (thanks to my references) so there is no quantum mystery here, so let's just move on.
Another make-believe idea in your head, never said, or even thought, by me. I understand two-particle entanglement, and I understand classical limits, and I understand the difference. It is you who do not, and that is why you cannot understand, yet must instead insert your klunky caricatures in place of what was actually said.However you then claim that if a two-photon entangled trajectory was "measured" you would still find a classical flux analog (nope, you won't)
More make believe on your part. What thread have you been reading? Didn't someone just quote a rule of the internet that it is silly to make claims about what was said when it's right there in black and white? What I actually said about that experiment is:You also ignore the recent measurement of a QM wavefunction article, dismissing it as some silly people who can't understand the correspondence principle or similar (you need to be specific why you dismiss this experiment otherwise I have to portray you dismissing it for this reason)
No, actually I did not ever say that either. I do wonder what can be learned about them from a judicious understanding of the classical analogs Maxwell's equations might provide, and I suspect that there are indeed useful analogs there, but I certainly never said the experiments could be "explained" by them. Indeed, all I"ve ever claimed is that classical limits of such experiments can be understood classically, but you've never really appreciated that nuance, or indeed almost any nuance of my argument.And you have also claimed that delayed choice experiments can be explained by maxwell's equations
Whether or not there are classical analogs of entanglement that could be informative is not yet clear. But there certainly are classical analogs to the wavefunction, indeed that's the whole reason it is called a wavefunction in the first place (and classical analogs is exactly how Schroedinger arrived at his celebrated equation in the first place). There certainly is a long history of using insights from classical analogs in quantum mechanics.unusualname said:I don't understand you because there is no classical limit related to entanglement, the wavefunction or delayed choice experiments.
So what on Earth are you talking about?
Just ask Schroedinger, it worked for him.The whole point of QM is that it is a spectacularly non-classical theory of nature, why would anyone want to emphasize classical limits?
Let's agree that the usefulness of classical analogs is something that is better demonstrated than postulated. I really was only using classical analogs to show that average trajectories are not strictly quantum mechanical objects because they don't apply to quanta, they apply to ensembles of quanta and so are amenable to being understood with classical-wave analogs.I suspected you got carried away with a partly reasonable anti-bohmian stance which seems to have developed over several threads into an "everything has a classical analog if you look at it from a certain point of view" argument.