Find a 95% confidence interval for population mean

[chwala]

Homework Statement

see attached

Relevant Equations

t distribution

I am refreshing on this...

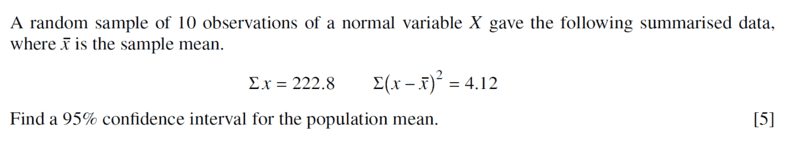
I think there is a mistake on the circled part in red...right? not correct symbol for sample mean...This is the part that i need clarity on.

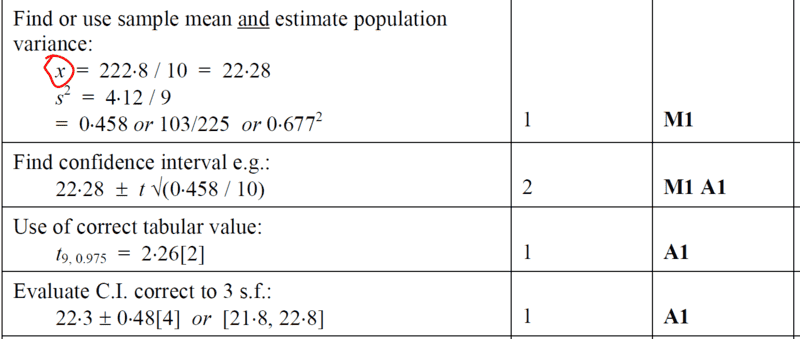
The other steps to solution are pretty easy to follow...as long as one knows the t-formula and also the knowledge to interpret the t-distribution table with dof_{1} = $9$ and significance level i.e dof_{2}= $0.025$ that gives us the desired $2.262$.

cheers

 

[Mark44]

The calculation is fine. The only thing I see wrong is that they wrote x for the sample mean instead of $\bar x$. Possibly a typo or maybe the author is unable to write this symbol.

 

[chwala]

The calculation is fine. The only thing I see wrong is that they wrote x for the sample mean instead of $\bar x$. Possibly a typo or maybe the author is unable to write this symbol.

@Mark44 This is from a Further Maths Examination Paper Mark scheme.