noowutah
- 56
- 3
TL;DR Summary: Find the electric field of a long line charge at a radial distance where the potential is 24V higher than at a radial distance r_1=3m where E=4V/m. Answer: 29.5V/m.
Never mind: I retract this question. The integral apparently is supposed to diverge! I apologize for not reading https://physics.stackexchange.com/questions/407797/potential-due-to-line-charge before I posted my question.
I am reading the book Electromagnetics with Applications by Kraus and Fleisch and have run into a snag with Problem 2-3-4.
For a line charge, the electric field is
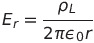
(rho_L is the linear charge density). Since we know E_r=4 at r=3, we can calculate rho_L=6.7*10^-10. To calculate the potential at r=3, I use
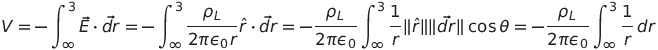
but this integral diverges ... where did I go wrong? \hat{r} is the unit vector orthogonal to the line.
Never mind: I retract this question. The integral apparently is supposed to diverge! I apologize for not reading https://physics.stackexchange.com/questions/407797/potential-due-to-line-charge before I posted my question.
I am reading the book Electromagnetics with Applications by Kraus and Fleisch and have run into a snag with Problem 2-3-4.
Find the electric field of a long line charge at a radial distance where the potential is 24V higher than at a radial distance r_1=3m where E=4V/m. Answer: 29.5V/m.
For a line charge, the electric field is
(rho_L is the linear charge density). Since we know E_r=4 at r=3, we can calculate rho_L=6.7*10^-10. To calculate the potential at r=3, I use
but this integral diverges ... where did I go wrong? \hat{r} is the unit vector orthogonal to the line.
Last edited by a moderator: