Finding the work done by Spiderman

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

The answer is $-4.70 kJ$. I am not sure what I am doing wrong.

My working is

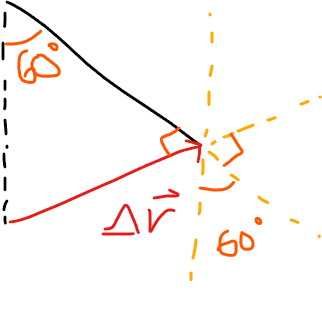
$W = mgr\cos\theta$
$W = mgr\cos150$ (since angle between $\vec g$ and $\vec r$ is 150 degrees)
$W = -mgr\frac {\sqrt{3}}{2}$
$W = -mgr\frac {\sqrt{3}}{2}$
$W = (-80)(9.81)(12\sin60)(\frac {\sqrt{3}}{2})$
$W = -7063.2 J$

Would some please be to offer some guidance?

Many thanks!

 

[haruspex]

$W = mgr\cos\theta$

Justify that.

 

[Lnewqban]

Please, attached diagram.

 

[member 731016]

Thank you for your replies @haruspex and @Lnewqban!

$W = \vec F \times \vec r$
$W = Fr\cos\theta$ from definition of dot product
F = mg since we are finding work done gravity
$W = mgr\cos\theta$

Many thanks!

 

[haruspex]

$W = \vec F \times \vec r$

No, that’s the cross product. You want the dot product.
But leaving that aside, what relationship does $\vec r$ need to have to the force in order for the result to be work done by the force?

 

[member 731016]

No, that’s the cross product. You want the dot product.
But leaving that aside, what relationship does $\vec r$ need to have to the force in order for the result to be work done by the force?

Sorry, yeah I forgot to do the dot product.

$\vec r$ can be at any angle expect $\theta = 90, 270, 450, n + 180$ with the force

Many thanks!

 

[PeroK]

I suggest you redo the problem with 1 degree rather than 60 degrees and you should see your mistake.

 

[haruspex]

$\vec r$ can be at any angle expect $\theta = 90, 270, 450, n + 180$ with the force

No, I mean the functional relationship. "$\vec r$ is the displacement through which …".

 

[member 731016]

I suggest you redo the problem with 1 degree rather than 60 degrees and you should see your mistake.

Thank you @PeroK! I have tried that now. I got a number much under the answer now.

Many thanks!

 

[member 731016]

No, I mean the functional relationship. "$\vec r$ is the displacement through which …".

Thank you @haruspex! Spider man moves?

Thank you !

 

[haruspex]

Thank you @haruspex! Spider man moves?

Thank you !

Wait, I'm sorry - I have objected to the wrong line.
It's this one:

$W = mgr\cos150$ (since angle between $\vec g$ and $\vec r$ is 150

Not according to your diagram.

 

[Lnewqban]

Thank you for your replies @haruspex and @Lnewqban!

$W = \vec F \times \vec r$
$W = Fr\cos\theta$ from definition of dot product
F = mg since we are finding work done gravity
$W = mgr\cos\theta$

Many thanks!

Who is F and who is W in your diagram?

The weight of Spiderman, force which has done some work, has a unique direction of action: vertical.

 

[member 731016]

Thank you for your replies @haruspex and @Lnewqban!

Sorry I don't understand how the angle between the line extending from the displacement vector and the force of gravity is not 150 degrees.

I think I must have got the angles wrong or something in the diagram. Could someone please show me how to correctly calculate the angle between the displacement and weight vector?

F is the force of gravity acting on spider man and W is the work done by the force of gravity on the spider man.

Many thanks!

 

[nasu]

You have a triangle with two equal sides (length of the wire in the two positions) and 60 degree angle at the top. What are the other two angles?

 

[member 731016]

You have a triangle with two equal sides (length of the wire in the two positions) and 60 degree angle at the top. What are the other two angles?

Thank you for your reply @nasu!

I did not see that it was an isosceles triangle! The two other angles will be 60 degrees each.

I will redo my diagram now.

Many thanks!

 

[nasu]

Actually is equilateral, isn't it?

 

[member 731016]

Actually is equilateral, isn't it?

Thank you for your reply @nasu!

True, you are right! I did not know that an equilateral triangle is a special case of an isosceles triangle!

Many thanks!

 

[member 731016]

Here is the new diagram with the equilateral triangle:

It still seems to give $\theta = 150$ thought. I'm still not sure, how to find the correct $\theta$.

Many thanks!

 

[haruspex]

Here is the new diagram with the equilateral triangle:
View attachment 322451
It still seems to give $\theta = 150$ thought. I'm still not sure, how to find the correct $\theta$.

Many thanks!

What makes you think the angle between the mg line and the dashed orange line that goes up to the right is 90°?

 

[nasu]

There are no 90 degrees angles, as you mistakenly show in your first diagram. How can you get 150?

 

[member 731016]

What makes you think the angle between the mg line and the dashed orange line that goes up to the right is 90°?

Thank your for your reply @haruspex !

Sorry, I did not mean the angle between the mg line at the dashed orange line at 90 degrees. It should be,

Many thanks!

 

[member 731016]

There are no 90 degrees angles, as you mistakenly show in your first diagram. How can you get 150?

Thank you for your reply @nasu!

Sorry, what do you mean there are no 90-degree angles?

I got 150 degrees since there is a right angle between the two dotted orange lines and a 60 degree angle between and the red mg line and dotted orange line.

Many thanks!

 

[haruspex]

Thank your for your reply @haruspex !

Sorry, I did not mean the angle between the mg line at the dashed orange line at 90 degrees. It should be,
View attachment 322454

Many thanks!

Ok, but how do you get 60° between mg and the lower dashed orange line?
It would help if you were to draw it a bit more accurately.

 

[nasu]

Thank you for your reply @nasu!

Sorry, what do you mean there are no 90-degree angles?

I got 150 degrees since there is a right angle between the two dotted orange lines and a 60 degree angle between and the red mg line and dotted orange line.

Many thanks!

No, there is not. What is that dotted orange line? If you draw it perpendicular ot the direction of $\Delta \vec{r}$ then the other angle is not 60 degrees. But you don't need that dotted line. Just draw the weight where $\Delta \vec{r}$ starts.

 

[member 731016]

Ok, but how do you get 60° between mg and the lower dashed orange line?
It would help if you were to draw it a bit more accurately.

Thank you for your reply @haruspex!

I think I got 60 degrees from the corresponding angles theorem.

Many thanks!

 

[member 731016]

No, there is not. What is that dotted orange line? If you draw it perpendicular ot the direction of $\Delta \vec{r}$ then the other angle is not 60 degrees. But you don't need that dotted line. Just draw the weight where $\Delta \vec{r}$ starts.

Thank you for your reply @nasu! I will do that.

Many thanks!

 

[nasu]

Thank you for your reply @haruspex!

I think I got 60 degrees from the corresponding angles theorem.
View attachment 322462

Many thanks!

That angle is 60 degrees but the extension of the black line is not along the dotted line that you show in the previous drawing. You see here that the black line is not at 90 degrees relative to this dotted orange line.

 

[haruspex]

You keep bending lines.
Go back to your diagram in post #1, draw it accurately, and don't mark in right angles that you cannot prove are right angled.

 

[member 731016]

Thank you for your replies @nasu and @haruspex !

Here is the new diagram,

How is it?

Many thanks!

 

[haruspex]

Thank you for your replies @nasu and @haruspex !

Here is the new diagram,
View attachment 322465
How is it?

Many thanks!

More accurate in some ways, but you have not marked in any angles, and you have moved the mg line over to the left.

 

[member 731016]

More accurate in some ways, but you have not marked in any angles, and you have moved the mg line over to the left.

Thank you for your reply @haruspex ! I moved the mg line to the left so I could see from exterior angle theorem that $\theta = 120~degrees$.

What way were you going to find the angle?

I think I also found $\vec {\Delta r}$ vector correctly now.

To find it I split my equilateral triangle into half to form a right angle triangle

I then found the opposite to be 6m so the total displacement must be 12m. But I guess I did not need to do that since the triangle has equal sides.

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex ! I moved the mg line to the left so I could see from exterior angle theorem that $\theta = 120~degrees$.

What way were you going to find the angle?

I think I also found $\vec {\Delta r}$ vector correctly now.

To find it I split my equilateral triangle into half to form a right angle triangle
View attachment 322466
I then found the opposite to be 6m so the total displacement must be 12m. But I guess I did not need to do that since the triangle has equal sides.

Many thanks!

Ok, so what is the angle between the force mg and the displacement $\vec r$?

 

[nasu]

"Equilateral" means all sides are the same size (equal sides). You don't need to split it and to form right angle triangles. You seem to have a tendency to pick the most complicated ways to solve things.,

 

[Steve4Physics]

Hi @Callumnc1. I’d like to mention an alternative method.

Do you know how to find (changes in) gravitational potential energy? If so, you can use:

Work done by gravity = - (change in gravitational potential energy)

It’s well worth thinking about why the above method is equivalent to the ‘dot product’ method.

 

[Lnewqban]

Thank you for your replies @haruspex and @Lnewqban!
...
F is the force of gravity acting on spider man and W is the work done by the force of gravity on the spider man.

How are those two forces different?
Acting only vertically, weight can only resist vertical displacement between lowest and highest points.
The muscular energy from Spiderman is the only cause of the horizontal displacement (r→), about which the problem is not asking.
Re-visit post #3 and focus only on pure vertical work.