- #1
santoki
- 34
- 0
forces -- A block slides upward on a rough, vertical wall
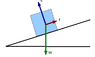
A block slides upward on a rough, vertical wall at constant velocity when a force F of 60 N acts on it at an angle Ɵ = 60ᵒ to the horizontal. The mass of the block is 3.0 kg. See picture below.

a) Using Newton’s laws, find the normal force on the block.
b) Determine the force of kinetic friction on the block.
2. The attempt at a solution
a) N = mg - Fy = (3.0)(9.8) - 60sin60° = -23
b) Fcos60° - μN = 0
60cos60° + 23μ = 0
μ = -1.3
a negative coefficient?
Homework Statement
A block slides upward on a rough, vertical wall at constant velocity when a force F of 60 N acts on it at an angle Ɵ = 60ᵒ to the horizontal. The mass of the block is 3.0 kg. See picture below.
a) Using Newton’s laws, find the normal force on the block.
b) Determine the force of kinetic friction on the block.
2. The attempt at a solution
a) N = mg - Fy = (3.0)(9.8) - 60sin60° = -23
b) Fcos60° - μN = 0
60cos60° + 23μ = 0
μ = -1.3
a negative coefficient?