bobie
Gold Member
- 720
- 2
A.T. said:Friction with a static object can't be a source of energy. In a reference frame where the ground moves, friction with the ground can do positive work.
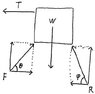
I made a sketch examining the 3 possible positions. Can you give it a look?
three positions
I am not sure what happens in sketch C:
if the weight 600N is all on the right leg, there is no component on the front foot, both diagonally and horizontally. Of course there is not equilibrium. But what really happen?
I imagine that the pull on the rope will generate a torque and the man will move up/left in a circle, but immediately his weight will bring him down. Will he oscillate or what? it's really intriguing.
How do I attach a thumbnail?
Thanks