Halliday, Resnick & Krane Chapter 5: Force on Pulley

[vibha_ganji]

Homework Statement

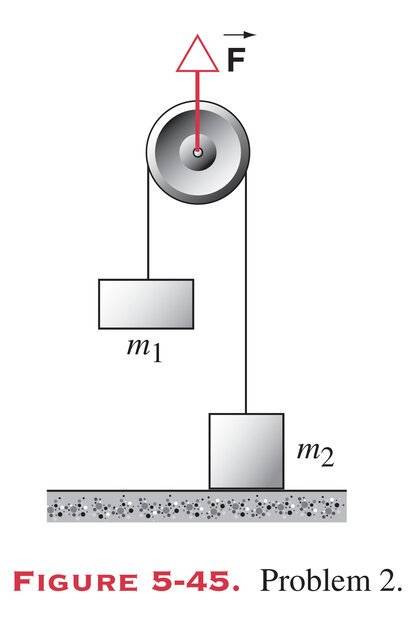
Someone exerts a force F directly up on the axle of the pulley shown in Fig. 5-45. Consider the pulley and string to be massless and the bearing frictionless. Two objects, m1 of mass 1.2 kg and m2 of mass 1.9 kg, are attached as shown to the opposite ends of the string, which passes over the pulley. The object m2 is in contact with the floor. (a) What is the largest value the force FB may have so that m2 will remain at rest on the floor? (b) What is the tension in the string if the upward force F is 110 N? (c) With the tension determined in part (b), what is the acceleration of m1?

Relevant Equations

F=ma
Force on pulley = 2(tension)

As the force on a pulley is equal to twice the tension, I just have to find the tension to solve part A. To do so, I first wrote the equations for both m1 and m2.

m1 * a = T - m1g

m2 * a = T + N - m2g

The tension must have the same values for both equations so I added both equations to find the tension.

m1a + m2a = 2T + N - g(m1 + m2)
a(m1+m2) + g(m1+m2) = 2T + N

(a+g)(m1+m2) - N = 2T

I’m not sure what to do next. Can I have a hint?

 

[haruspex]

m1 * a = T - m1g

m2 * a = T + N - m2g

How are you defining a? Will the masses have the same acceleration?