cbarker1
Gold Member
MHB
- 345
- 23
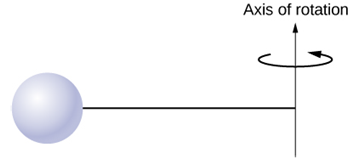
A sphere of mass 1.9 kg and radius 0.5 m is attached to the end of a massless rod of length 3.0 m. The rod rotates about an axis that is at the opposite end of the sphere (see below). The system rotates horizontally about the axis at a constant 422 rev/min. After rotating at this angular speed in a vacuum, air resistance is introduced and provides a force 0.23 N on the sphere opposite to the direction of motion. What is the power (in W) provided by air resistance to the system 167.0 s after air resistance is introduced? (Enter the magnitude.)
Work
$$I_(new)=2/5mR^2+M(3.5)^2$$= 23.465
$$3.5F_f=I\alpha$$=.034306
$$\alpha=3.5F_f/I$$
$$\omega_0=2\pi/60*422rpm$$=44.19
$$\omega=\omega_0+\alpha*167$$=49.878
$$P=F_f*\omega$$=11.4719
What did I done wrong? Thanks

Work
$$I_(new)=2/5mR^2+M(3.5)^2$$= 23.465
$$3.5F_f=I\alpha$$=.034306
$$\alpha=3.5F_f/I$$
$$\omega_0=2\pi/60*422rpm$$=44.19
$$\omega=\omega_0+\alpha*167$$=49.878
$$P=F_f*\omega$$=11.4719
What did I done wrong? Thanks
Last edited: