I How fast does a blastwave travel?

[Squizzie]

The Mach number there refers to the speed of an aerodynamic vehicle, not to the speed of sound wave propagation. The aerodynamics of the vehicle change as it approaches the speed of sound, which is slower in the cold at higher altitudes.

Yes, I know.
All I'm trying to do is establish that once the blast wave has detached from the detonation phase, i.e. after a few milliseconds, or, in the case of a nuclear detonation a second or so, under normal atmospheric conditions, such as the case of the Beirut explosion, the blast wave then propagates at approximately 340 m/sec, or Mach 1.0.

 

[Baluncore]

All I'm trying to do is establish that once the blast wave has detached from the detonation phase, i.e. after a few milliseconds, or, in the case of a nuclear detonation a second or so, under normal atmospheric conditions, such as the case of the Beirut explosion, the blast wave then propagates at approximately 340 m/sec, or Mach 1.0.

Why do you try to establish that falsehood?

Outside the explosive combustion products, the supersonic shock front, is part of the blast wave.

https://en.wikipedia.org/wiki/Brandolini's_law
Brandolini's Law: “The amount of energy needed to refute bullshit is an order of magnitude bigger than that needed to produce it”.

 

[Squizzie]

Outside the explosive combustion products, the supersonic shock front, is part of the blast wave.

Could you please specify where and when the blast wave starts propagating from the detonation centre using the attached figure and data?

 

[Baluncore]

You are plotting three sets of data there, each is a different magnitude, varying over a factor of maybe 1000. There is no one point on that plot, and because it is a Log-Log plot, the traces cannot be moved into alignment.

 

[Squizzie]

You are plotting three sets of data there, each is a different magnitude, varying over a factor of maybe 1000. There is no one point on that plot, and because it is a Log-Log plot, the traces cannot be moved into alignment.

Could you please specify where and when the blast wave starts propagating from the detonation centre on any of the three data sets?

 

[Squizzie]

You are plotting three sets of data there, each is a different magnitude, varying over a factor of maybe 1000. There is no one point on that plot, and because it is a Log-Log plot, the traces cannot be moved into alignment.

Here are my estimates of the (time, distance) coordinates of the shock fronts' transition to Mach 1.0.

Please can you indicate where you believe the blast waves originate?

 

[Baluncore]

Please can you indicate where you believe the blast waves originate?

The blast wave begins with the first recorded point on your graphs, at the point of maximum shock front velocity in air. The point you mark on the blast wave, is where the shock front ceases to exist. The blast does not begin at your marker, nor does it end there.

When it comes to the definition of a blast wave, the 1947, Los Alamos paper "Blast Wave", LA-2000, discusses shock fronts that are certainly the most interesting part of the blast wave.

The problem with specifying the start of the blast wave, is that no local instrumentation can survive in proximity with the detonation. Observation of that critical point must be remote and optical, perpendicular to the opaque detonation surface.

The precise origin point of the blast wave, that I would select, is where the shock front, in "transparent air", first separates from the "opaque combustion products". Before that point the contact surface is accelerating, after that point it is a decelerating shock front.

 

[Squizzie]

The blast wave begins with the first recorded point on your graphs, at the point of maximum shock front velocity in air. The point you mark on the blast wave, is where the shock front ceases to exist. The blast does not begin at your marker, nor does it end there.

When it comes to the definition of a blast wave, the 1947, Los Alamos paper "Blast Wave", LA-2000, discusses shock fronts that are certainly the most interesting part of the blast wave.

The problem with specifying the start of the blast wave, is that no local instrumentation can survive in proximity with the detonation. Observation of that critical point must be remote and optical, perpendicular to the opaque detonation surface.

The precise origin point of the blast wave, that I would select, is where the shock front, in "transparent air", first separates from the "opaque combustion products". Before that point the contact surface is accelerating, after that point it is a decelerating shock front.

While I agree with you that the Los Alamos paper makes good reading (reference [1] my post #194 and source of my "Los Alamos" data) and that "The precise origin point of the blast wave… is where the shock front, in 'transparent air', first separates from the 'opaque combustion products'", there are significant divergences in our viewpoints on numerous aspects.
Given the extent of our disagreements, I suggest we respectfully agree to disagree and leave the matter for our peers to review and adjudicate.

 

[Baluncore]

Given the extent of our disagreements, I suggest we respectfully agree to disagree and leave the matter for our peers to review and adjudicate.

Ever since post #7, and it is now more than 200 posts later, you have been insisting that the supersonic shock front is NOT part of the blast wave. That is quite contrary to all the literature, so I must disagree with you on your personal definition of a blast wave. You can disagree, and walk away. I will agree not to follow you.

 

[Squizzie]

I hesitate to use the term 'blast wave' to encompass both the supersonic and the sonic phases due to its potential to mask fundamental differences in the physics at the interface. I refer to Kinney and Graham for this distinction, though similar information can be found in various references.
In the supersonic phase, a thin region exists between the hot, high-pressure gas on the detonation side of the shock and the ambient air through which the shock is travelling, as illustrated in Fig 4-2 below

The interface between a discontinuity in a gas with different state variables is described by the Rankine-Hugoniot condition. This condition is characterised by a set of equations that offer a mathematical model for the process.

The separate sonic phase is characterised by a pressure wave featuring a sharp, almost instantaneous rise in pressure, followed by a smooth reduction back to ambient pressure, as illustrated in Fig 6-3 below:

It also includes a "negative phase"in which the pressure reduces to below ambient pressure.
This shape has been mathematically modelled using the Friedlander equation, and I will refer to it by that name.
As is commonly practised, the depiction of the blast wave often employs a time scale, in contrast to the distance scale used earlier. When both phenomena are graphed on the same set of axes, their distinctions become readily apparent, as illustrated below

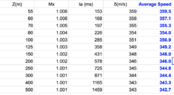
While the following table applies to both high explosives such as TNT, C4, and NH4, as well as nuclear explosions, the substantial variation in process intensity may make numerical comparisons somewhat obscure.

Properties​	Phase​	Phase​
	"Hugoniot"​	"Friedlander"​
Propagation speed	Decelerating from hypersonic to sonic.	Steady, Mach 1.0
Conditions on blast side the shock	High pressure, hot.	Atmospheric pressure and temperature
Lifetime, seconds	Very brief:<=10-2 for chemical, <=10 for nuclear	Long: > 102
Propagation distance, metres	Very short: <=102 chemical, <=103 nuclear	Long: > 103
Survivable?	No	Yes

I suggest that the term 'detonation phase' be reserved for the brief, supersonic 'Hugoniot' phase, while 'blast wave' is more appropriately used for the extended sonic 'Friedlander phase' due to these distinctions.

 

[Baluncore]

It is not your prerogative to invalidate the literature of science, by demanding your personal terminology replace that employed for the last century.

 

[renormalize]

I suggest that the term 'detonation phase' be reserved for the brief, supersonic 'Hugoniot' phase, while 'blast wave' is more appropriately used for the extended sonic 'Friedlander phase' due to these distinctions.

With just a few minutes of googling, I easily find references (with my emphasis added) that directly contradict your "appropriate distinctions".

https://en.wikipedia.org/wiki/Blast_wave:

https://apps.dtic.mil/sti/pdfs/AD0608861.pdf:

https://onlinelibrary.wiley.com/doi/abs/10.1002/prep.201400042:

Can you cite any reference that supports your "distinction", i.e., one that explicitly and unequivocally states that a "blast wave" travels only at the speed of sound (or less)? If not, you're simply espousing a personal theory that contradicts the literature.

 

[Drakkith]

I suggest that the term 'detonation phase' be reserved for the brief, supersonic 'Hugoniot' phase, while 'blast wave' is more appropriately used for the extended sonic 'Friedlander phase' due to these distinctions.

I see no reason to do this, especially since the term 'phase' can be and is used to mark the distinctions. The term 'blast wave' appears to be a more general term for how the resulting shock wave and field flow is generated, with the aforementioned phases used to describe the different parts of the blast wave.

Please use the standard terminology in discussing this topic.

 

[Squizzie]

I see no reason to do this, especially since the term 'phase' can be and is used to mark the distinctions. The term 'blast wave' appears to be a more general term for how the resulting shock wave and field flow is generated, with the aforementioned phases used to describe the different parts of the blast wave.

Please use the standard terminology in discussing this topic.

While the term 'blast wave' is commonly used to describe the entire phenomenon, it's important to recognize that the blast wave actually consists of two distinct phases, each with its own unique characteristics of propagation speed and pressure profile.
The first phase is characterised by a very high initial propagation speed which decays within milliseconds to the speed of sound, with an abrupt pressure rise, while the second phase exhibits a slower, more gradual decay in pressure and a constant propagation speed.

Unfortunately, a standardised terminology for each of these phases is lacking, introducing challenges into discussions about the speed of a blast wave.

 

[renormalize]

While the term 'blast wave' is commonly used to describe the entire phenomenon, it's important to recognize that the blast wave actually consists of two distinct phases, each with its own unique characteristics of propagation speed and pressure profile.
The first phase is characterised by a very high initial propagation speed which decays within milliseconds to the speed of sound, with an abrupt pressure rise, while the second phase exhibits a slower, more gradual decay in pressure and a constant propagation speed.

You keep claiming this but you haven't answered my request from post #212. Again I implore you: please support your claim by posting references that explicitly define this "second phase" of a blast wave and explicitly state that the propagation velocity of a blast wave rapidly decays to, and then continues to propagate at, a constant speed of Mach 1. Or is this really just a personal interpretation of what you've read?

 

[Squizzie]

You keep claiming this but you haven't answered my request from post #212. Again I implore you: please support your claim by posting references that explicitly define this "second phase" of a blast wave and explicitly state that the propagation velocity of a blast wave rapidly decays to, and then continues to propagate at, a constant speed of Mach 1. Or is this really just a personal interpretation of what you've read?

May I direct your attention to my post #206, where I presented a plot featuring data sets from three reputable sources? I have adopted a log scale for both axes in order to accommodate the vast scale range of the two co-ordinates.
In that log/log scale, constant speeds can be represented by parallel lines as indicated by the dotted lines.
The plot illustrates the position of the shock front over time and distance from the detonation. In all three plots, a discernible transition between two phases is evident.
During the initial phase, the shock front speed undergoes a decay from an initial hypersonic speed to a consistent speed of approximately 340 m/s (Mach 1.0 at NTP).
In the second phase, it travels at that constant speed (340 m/s) to the remainder of the data.

 

[Baluncore]

I suggest that the term 'detonation phase' be reserved for the brief, supersonic 'Hugoniot' phase, while 'blast wave' is more appropriately used for the extended sonic 'Friedlander phase' due to these distinctions.

The Rankine–Hugoniot conditions, describe and model the pressure step transition at one point, only as the shock front pressure rises. The blast-wave air-movement that follows the shock front, is not covered by that analysis.

Friedlander models the pressure at one place, near the explosion, over time. It covers the period from the shock front passing that place, right through to the relaxation at the end of the negative phase in that place. Friedlander models the pressure against time, NOT against distance.

After the event, examination of blast damage, does NOT identify the presence of a shock front. The sum of all damage, caused by the pressure changes, or the
blast wave winds, is all undifferentiated blast damage.

The detonation front, or detonation wave, already refers to the progress of the chemical reaction through the explosive material. The atmosphere certainly does NOT detonate, as a shock front passes.

Your choice of terms to be redefined and reallocated, seem inappropriate, and selected to cause maximum possible confusion in the literature. I cannot help thinking that, to consider such a change, you must be equally confused in your understanding.

 

[renormalize]

May I direct your attention to my post #206, where I presented a plot featuring data sets from three reputable sources? I have adopted a log scale for both axes in order to accommodate the vast scale range of the two co-ordinates.

That's a plot you made. I ask for the original references, not filtered through your personal interpretation, that explicitly state that 1) there are two phases of blast waves and 2) the second phase propagates at a constant Mach 1.

 

[Drakkith]

Unfortunately, a standardised terminology for each of these phases is lacking, introducing challenges into discussions about the speed of a blast wave.

Look, I don't really care what else you call it, but trying to use 'blast wave' to describe only one part of the process, when it is commonly used to describe the entire thing from creation to dissipation, is only going to generate confusion.

You keep claiming this but you haven't answered my request from post #212. Again I implore you: please support your claim by posting references that explicitly define this "second phase" of a blast wave and explicitly state that the propagation velocity of a blast wave rapidly decays to, and then continues to propagate at, a constant speed of Mach 1. Or is this really just a personal interpretation of what you've read?

From my reading, the blast wave quickly decays to the speed of sound in the (unheated, uncompressed) medium. You can check the links I posted previously in post #90.

I'd also like to remind people that communication is a two-way street. Describing and explaining phenomena is often difficult, even with the proper terminology readily available, and it is often more beneficial to take the time to try to understand what someone is trying to say versus taking what they typed out at literal value. Also, there is no harm in agreeing on a 'temporary' set of terms to use for a discussion if such a thing is warranted.

 

[renormalize]

From my reading, the blast wave quickly decays to the speed of sound in the (unheated, uncompressed) medium. You can check the links I posted previously in post #90.

I agree, except that, according to the quotes in post #212, a propagating atmospheric disturbance is not called a "blast wave" once it slows to the ambient speed of sound. It's no longer a "blast wave" because it is no longer accompanied by significant pressure excursions, else it wouldn't be in "ambient conditions". The disturbance becomes an ordinary high-amplitude sound wave. That's why I ask @Squizzie to cite some references that uses "blast wave" to label a sonic-speed disturbance in ambient conditions.

 

[Squizzie]

Look, I don't really care what else you call it, but trying to use 'blast wave' to describe only one part of the process, when it is commonly used to describe the entire thing from creation to dissipation, is only going to generate confusion.

From my reading, the blast wave quickly decays to the speed of sound in the (unheated, uncompressed) medium. You can check the links I posted previously in post #90.

I'd also like to remind people that communication is a two-way street. Describing and explaining phenomena is often difficult, even with the proper terminology readily available, and it is often more beneficial to take the time to try to understand what someone is trying to say versus taking what they typed out at literal value. Also, there is no harm in agreeing on a 'temporary' set of terms to use for a discussion if such a thing is warranted.

Yes, you are correct, but in the absence of any other terminology, my approach has been to restrict my use of "blast wave" it to the much longer phase once it has decayed to the speed of sound. It is that phase that Kinney & Graham discuss in Ch 6. "Blast Waves".
After all this is the phase that lasts for many seconds whereas the earlier phase (which I have clumsily identified as the "detonation phase") only lasts milliseconds (but does most of the damage) .
I would welcome the opportunity to discuss alternate temporary set of terms.

 

[Drakkith]

I agree, except that, according to the quotes in post #212, a propagating atmospheric disturbance is not called a "blast wave" once it slows to the ambient speed of sound. It's no longer a "blast wave" because it is no longer accompanied by significant pressure excursions, else it wouldn't be in "ambient conditions". The disturbance becomes an ordinary high-amplitude sound wave. That's why I ask @Squizzie to cite some references that uses "blast wave" to label a sonic-speed disturbance in ambient conditions.

The blast wave appears to undergo an exponential decay towards the speed of sound, and I'm wondering if the shock front is sustained for a significant amount of time very close to the speed of sound before finally transitioning to a regular sound wave. I have yet to see anything in any of the sources I've read in this thread seen anything about when/where/how this transition occurs. That leads me to believe that the blast wave remains a blast wave for a pretty long time/distance and the transition to a sound wave is not particularly important. But that's a guess on my part.

Yes, you are correct, but in the absence of any other terminology, my approach has been to restrict my use of "blast wave" it to the much longer phase once it has decayed to the speed of sound. It is that phase that Kinney & Graham discuss in Ch 6. "Blast Waves".

I have yet to see anything that made any effort to use 'blast wave' differently in the two phases, so I would highly recommend not doing that. If you really need to label the two phases, perhaps 'early' and 'late' phases would be do, or "supersonic' and 'near-sonic', or something similar.

 

[Baluncore]

The blast wave appears to undergo an exponential decay towards the speed of sound, and I'm wondering if the shock front is sustained for a significant amount of time very close to the speed of sound before finally transitioning to a regular sound wave.

The shock front decays exponentially as it heats air, at the same time as it is attenuated by the inverse square law.

Gilbert F. Kinney and Kenneth J. Graham - Explosive Shocks in Air. 2'nd Edn. 1985.
Table XI, page 254, shows one kilogram of TNT as being supersonic to beyond 500 metres. From 100 m to 500 m, the velocity falls by only 0.2%.

I have yet to see anything in any of the sources I've read in this thread seen anything about when/where/how this transition occurs.

There is no clear point where the transition occurs. The two velocity modes are feathered together. I would expect reflections to make the transition quite patchy near the ground.

 

[Squizzie]

Gilbert F. Kinney and Kenneth J. Graham - Explosive Shocks in Air. 2'nd Edn. 1985.
Table XI, page 254, shows one kilogram of TNT as being supersonic to beyond 500 metres. From 100 m to 500 m, the velocity falls by only 0.2%.

By computing the speed between each pair of data points using V_i = (Z_i - Z_i-1) / (t_i- t_i-1) with the provided data, you will observe a consistent interval speed of 340 m/s from 70 metres to 500 metres.

Could you please provide more details about the meaning and implications of the "only 0.2%?"

 

[Frabjous]

By computing the speed between each pair of data points using Vi = (Zi - Zi-1) / (ti- ti-1) with the provided data, you will observe a consistent interval speed of 340 m/s from 70 metres to 500 metres.

I do not understand why you are differentiating the data when the Mach number is given.

I've plotted the 1 kg HE data from Kinney. I plotted the full range of the Mach Number and a limited range of the Mach Number as a function of distance.

Please identify where you would start your "blast regime” given that the propagation speed is asymptoting to the sound speed.

Fun fact, the pressure of the last point is about 140 dB.

 

[Baluncore]

Could you please provide more details about the meaning and implications of the "only 0.2%" ?

They give the accurate velocity as a Mack number in the Mx column.
Z = 100 m; Mx = 1.003
Z = 500 m; Mx = 1.001
The difference is only 0.2%, but it is still supersonic at 500 m.

You are seeing numerical round-off noise from the tabulated data in your unnecessary re-computation. That explains why your graph jumps up and down about the speed of sound, while the shock front remains supersonic throughout.

 

[Squizzie]

They give the accurate velocity as a Mack number in the Mx column.
Z = 100 m; Mx = 1.003
Z = 500 m; Mx = 1.001
The difference is only 0.2%, but it is still supersonic at 500 m.

You are seeing numerical round-off noise from the tabulated data in your unnecessary re-computation. That explains why your graph jumps up and down about the speed of sound, while the shock front remains supersonic throughout.

But the difference between Mach 1.003 (at Z=100 m) and Mach 1 ( ~340 m/sec) is 1.02 metres per second. A few degrees of temperature or hectopascals of atmospheric pressure could easily account for those differences in the data.
I'm not convinced that this evidence is sufficient to support the conclusion that the shock front was moving at anything other than Mach 1.

 

[Baluncore]

I'm not convinced that this evidence is sufficient to support the conclusion that the shock front was moving at anything other than Mach 1.

Then you will be unable to work as a scientist in this field.
The data says it is doing Mx = 1.001, not Mx = 1.000
How can it be a shock front if it is not moving faster than Mach 1.

 

[Frabjous]

But the difference between Mach 1.003 (at Z=100 m) and Mach 1 ( ~340 m/sec) is 1.02 metres per second. A few degrees of temperature or hectopascals of atmospheric pressure could easily account for those differences in the data.
I'm not convinced that this evidence is sufficient to support the conclusion that the shock front was moving at anything other than Mach 1.

Well, there is also the theory, and I would also say that my plot of the data supports the conclusion.

 

[Squizzie]

How can it be a shock front if it is not moving faster than Mach 1.

I think we are both correctly interpreting the data in table XI as it relates to the progress of the shock front as explained on p. 96 of Chapter 6 "Blast Waves":
" the peak overpressure values of Table XI also uniquely define the time required for that shock front to travel out to various distances. "
And I have previously identified p. 88 of the same chapter:
"Each individual portion of this pulse moves outward at its own speed, which also is the speed of sound in its own immediate medium. "
So I'm not convinced that your evidence is sufficient to support your contrary conclusion that the shock front was propagating at anything other than steadily at Mach 1 by 100 metres and 280 ms.

 

[Frabjous]

I think we are both correctly interpreting the data in table XI as it relates to the progress of the shock front as explained on p. 96 of Chapter 6 "Blast Waves":
" the peak overpressure values of Table XI also uniquely define the time required for that shock front to travel out to various distances. "
And I have previously identified p. 88 of the same chapter:
"Each individual portion of this pulse moves outward at its own speed, which also is the speed of sound in its own immediate medium. "
So I'm not convinced that your evidence is sufficient to support your contrary conclusion that the shock front was propagating at anything other than steadily at Mach 1 by 100 metres and 280 ms.

No. You are proposing the nonstandard interpretation. The responsibility is on your end.

 

[Squizzie]

No. You are proposing the nonstandard interpretation. The responsibility is on your end.

Is not Kinney and Graham, from whom I'm drawing my reference, the standard text?

 

[Frabjous]

Is not Kinney and Graham, from whom I'm drawing my reference, the standard text?

Yes, and you are saying that the data they present is wrong. You did not know about it when you started this thread, and now you believe that you can correct it.

 

[Baluncore]

So I'm not convinced that your evidence is sufficient to support your contrary conclusion that the shock front was propagating at anything other than steadily at Mach 1 by 100 metres and 280 ms.

But a shock front is a pressure step that heats the air. It propagates faster in the heated air, so it maintains the step. The shock front must be propagating marginally above Mach 1, to remain as a step.

All things are relative. Small variations in local air pressure or temperature, do not influence the differential step height of the pressure or temperature shock.

You would find the distinct 'crack' of any shock front to be an uncomfortable noise, no matter how small it was.

You cannot round; Mx > 1, down to; Mx = 1, while the shock front remains a step, which the data shows it does, to beyond 500 metres.

By definition, NO shock front ever propagates at Mach 1.

 

[Squizzie]

Yes, and you are saying that the data they present is wrong.

If you are suggesting that I am contradicting the data in Table XI, I should point out that the"δ(m/s)" and "Mx" values reported in Table XI represent the average speed (Z(m)/ t_a), not the interval speed.

I attach a screenshot of my working, highlighting the detail that the δ(m/s) values in the table are in fact the average values that can be deduced from the data, not the interval values.

Since the speed is decreasing from an initially very high value, the average speed values will approach asymptotically to Mach 1, obscuring the fact that, as my post #224 above clearly shows, the interval, or instantaneous speed of Mach 1 is achieved after about 50 metres from the blast.

 

[Baluncore]

@Squizzie
Way back, about 200 posts ago, in post #24, you believed that you had estimated a shock front velocity to be about Mach 1. What you had actually estimated, was the phase velocity of the condensation cloud formation, in the inertially pulled depression that followed the explosion. At the time, that was one of the several things you did not know existed.

If you do not know what you are doing, you must be prepared to learn. There are early false beliefs, that you must dispel. One of those is your belief that a shock front propagates at Mach 1, which actually contradicts the definition of a shock wave. Maybe you would get a better perspective if you first studied the Dunning-Kruger effect.

Rather than study, accept, and work in the field, you deny and contradict the science, then like an authoritarian barbarian, a dictator, you persistently try to crush the science.

 

[Drakkith]

I think that's it for this thread.
@Squizzie Without any clear statement to the contrary from the references on the topic, I'm inclined to believe that the blast wave continues to travel just above the speed of sound until the energy dissipates. Even if only barely above the speed of sound.

If anyone finds a reference that clearly states otherwise, please feel free to PM myself or another mentor and we can discuss reopening the thread. Until then, thread locked.