jbriggs444 said:
I see the vehicle mass ("masse") is 830. Presumably in kilogram units. A small vehicle by U.S. standards.
Edit: The owner's manual for my own vehicle says 1570 kg, even though it is small by U.S. standards. It is a Honda Fit
I see that the initial velocity ("v0") is 50 kilometers per hour expressed as meters per second. A modest starting velocity and utterly irrelevant to the calculation at hand. We are not shown the conversion routine that computes the meters per second figure from the input of "50", but it is a good guess that this is 13.89 meters per second.
I see that the the tire's outer and inner radius ("rayon_pneu") and ("rayon_interiur") are taken from a lookup table (or a function evaluation) for a 155-65R14 tire. Nominally, those numbers indicate 155 mm tread width, a sidewall height of 65% of that (101 mm sidewall height), a wheel diameter of 14 inches. And radial construction. That is a wheel radius of 178 mm plus the sidewall height of 101 mm for a total radius of 279 mm if my calculations and understanding of tire naming is correct.
A variable named "largeur_bande" (English "band width") is also set to this figure of 279 mm.
One hopes that these variables are expressed in units of meters so that the variables will contain 0.279
A variable named "rayon_frein" (English "brake radius") is set to 80% of this figure.
I strongly agree with all of this
All my numbers are in SI units, so kilograms, meters...
Yes my car is very tiny, even by France standards
jbriggs444 said:
The brake disc (aka the "rotor") looks to be about 30 to 35% of the diameter of the tire. That is a crude estimate.
The rotor has to fit within the dimensions of the wheel. In my case with 15 inch (diameter) wheels, this would impose an absolute limitation of 7.5 inches. The need for additional clearance between the brakes and the wheel reduces this further.
The first reference I Googled up was from a Quora post where Kelli Hollinger said that "A small compact car with 14″ wheels can have a 10″ solid brake rotor". Generously, that would call for my rotor having an outside diameter of no more than 139 mm or about 45% of the tire radius.
The track of the brake pad on rotor will be less than this. So we have an error of somewhere between a factor of two and a factor of four in your calculations already, even without having seen them.
Okay, that's the first source of error, I supposed the caliper to be put on the outside of the rim, and it seems very true that it's not realistic this way, I will change *0.8 to *0.35
jbriggs444 said:
Please, for the love of God, can you actually produce a calculation to back up your claims.
jbriggs444 said:
What I see is 23 lines of code. The comments are in French and I do not speak the language, so that will be a handicap.
I think you did not see the full code, so here it is again :
First: Parameters file
The calculation of a wheel moment of inertia is highlighted
[CODE lang="python" title="Parameters file" highlight="16"]from utils import *
masse = 830 # Masse de la voiture
v0 = kmh_vers_mps(50) # Vitesse initiale
rayon_pneu, rayon_interieur, largeur_bande = ref_roue_vers_dimensions('155-65R14')
rayon_frein = rayon_interieur * 0.8 # Approximation de la distance par rapport à l'axe où la pression est appliquée
n_roues_actives = 2 # Nombre de roues actives
#todo Ce paramètre va être retiré plus tard
mu_sol = 0.7 # Coefficient de friction entre la roue et le sol
pression_freins = bar_to_pascal(7) # Pression de freinage
surface_plaquette = 0.0057390 # Surface d'une plaquette de frein
masse_roue = 6 # Masse de la roue
moment_inertie_roue = (masse_roue * (rayon_pneu**2 - rayon_interieur**2)) / 2 # Moment d'inertie de la roue
t_reaction = 1 # Temps de réaction du conducteur
x = 0 # Position initiale
v = v0 # Vitesse initiale
a = 0 # Acceleration initiale
t = 0 # Temps initial
# Il faut un pas de temps pour que dv << v
dt = 0.001[/CODE]
Second: Useful functions and variables
It contains the gravity constant, the zero-limit of comparison, a function to get measurements of a wheel based on the reference, and various converting functions
[CODE title="Utils file"]limite_zero = 10**-16
g = 9.81
def ref_roue_vers_dimensions(roue):
"""
Convertit une référence de pneu en un rayon et une largeur
Les références sont du type A-BRC avec
A : Largeur de la roue en cm
B : Ratio hauteur de la bande/largeur
C : Diamètre de la jante en pouces
"""
largeur_cm, infos = roue.split('-')
ratio, diametre_jante = infos.split('R')
largeur = float(largeur_cm) / 100
diametre_jante = float(diametre_jante) / 0.0254
epaisseur = largeur * float(ratio)/100
rayon = diametre_jante / 2 + epaisseur
rayon_interieur = diametre_jante / 2
return rayon, rayon_interieur, largeur
def mps_vers_kmh(vitesse):
"""
Convertit une vitesse en m/s en km/h
"""
return vitesse * 3.6
def kmh_vers_mps(vitesse):
"""
Convertit une vitesse en km/h en m/s
"""
return vitesse / 3.6
def bar_to_pascal(pression):
"""
Convertit une pression en bar en pascal
"""
return pression * 100000[/CODE]
And the most important: The main file
The lines with the calculation loop are highlighted
I know this loop is not optimized, but I keep it like this for consistency with further steps.
[CODE title="Main file" highlight="28-46"]from utils import *
from matplotlib import pyplot as plt
from parameters import *
#import pacejka###* Initialisation des tableaux de données
points_vitesse = [v0]
points_distance = [0]
points_temps = [0]###* Paramètres de la simulation
compter_temps_reaction = True # Si on compte le temps de réaction
afficher_vitesse = False # Si on affiche la vitesse
if compter_temps_reaction:
# Temps de réaction : 1s
for i in range(int(t_reaction / dt)):
t += dt
x += v0 * dt
points_distance.append(x)
points_vitesse.append(v0)
points_temps.append(t)###* Boucle principale de la simulation
while v > limite_zero:
t = t + dt
couple_freins = -2 * (pression_freins * surface_plaquette) * (rayon_frein / rayon_pneu)
#todo Il faut trouver un moyen de calculer d_theta
#slip = pacejka.calcul_derapage(v, d_theta, F_eq, dt)
#mu_sol = pacejka.calcul_mu(slip, *pacejka.coeffs_route_seche)
limite_glissement = -mu_sol * masse * g
if abs(couple_freins) > abs(limite_glissement):
F_eq = limite_glissement
else:
F_eq = couple_freins
M_eq = masse + n_roues_actives * moment_inertie_roue / rayon_pneu**2
a = F_eq / M_eq
v = v + a * dt
x = x + v * dt
points_distance.append(x)
points_vitesse.append(v)
points_temps.append(t)
###* Post-traitement des données
points_vitesse = [mps_vers_kmh(v) for v in points_vitesse] # On convertit les vitesses en km/h
# On affiche ou pas certaines données
fig, ax = plt.subplots()
ax.plot(points_temps, points_distance, color='b')
ax.set_xlabel('Temps (s)')
ax.set_ylabel('Distance (m)', color='b')
ax.tick_params('y', colors='b')
# Afficher la vitesse est facultatif
if afficher_vitesse :
ax2 = ax.twinx()
ax2.plot(points_temps, points_vitesse, 'r')
ax2.set_ylabel('Vitesse (km/h)', color='r')
ax2.tick_params('y', colors='r')
# On marque la distance de freinage en texte sur le graphique
# Le texte est encadré dans un cadre avec des coins arrondis
# Le texte est en bleu
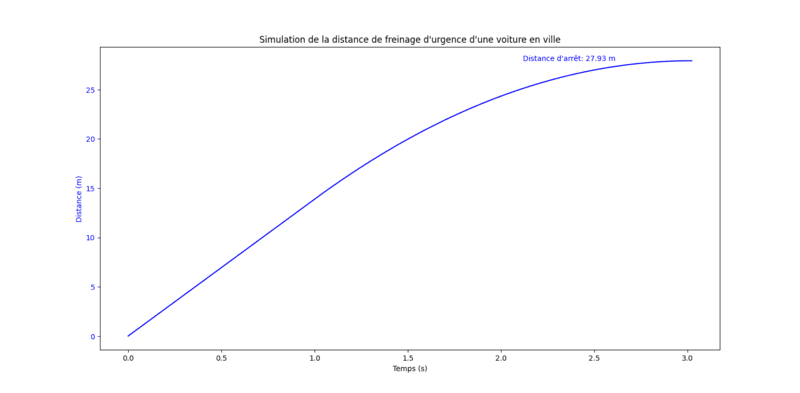
ax.text(0.7*points_temps[-1], points_distance[-1], 'Distance d\'arrêt: ' + str(round(points_distance[-1], 2)) + ' m',
bbox={'facecolor':'0000', 'alpha':0.0, 'pad':10}, color='b')
plt.title('Simulation de la distance de freinage d\'urgence d\'une voiture en ville')
plt.show()[/CODE]
I'm again sorry because my code is in french and you don't speak the language, but sadly I have to make it this way...
I still have to thank you all for not having made those suptid jokes (baguette hu hu), that sadly are legion