How to calculate the mass of gas in a tank?

[Chestermiller]

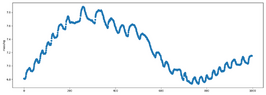
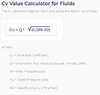
No. What I mean is that I could for example measure a temperature of 25°C with a pressure of 10bar, then 26°C with a pressure of 8bar, 24°C with 4bar, 25°C with 2bar and so on. So what I mean is that my measurements may not be close to the line I calculated in post #32.

Is this what you are measuring inside the tank?

 

[Leopold89]

Somwhat yes. I have also included a plot of my data of one gas tank.

Edit: I think I understand now. The integrated curve is the same as the p-T-curve in the phase diagrams, so once I am above or below it, the model has to change between a pure liquid, a liquid-vapour mixture and a pure vapour/gas, right?

 

[Chestermiller]

Somwhat yes. I have also included a plot of my data of one gas tank.

Edit: I think I understand now. The integrated curve is the same as the p-T-curve in the phase diagrams, so once I am above or below it, the model has to change between a pure liquid, a liquid-vapour mixture and a pure vapour/gas, right?

Yes.