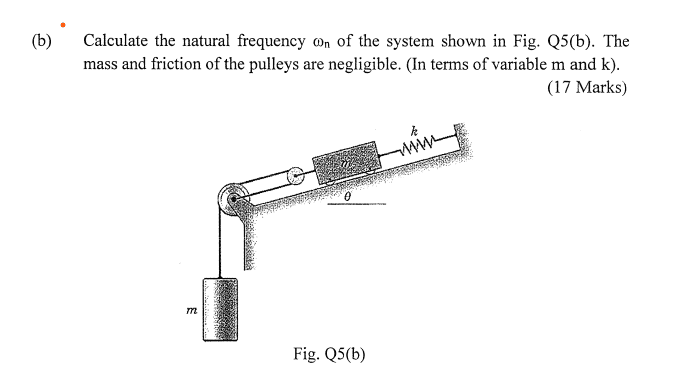
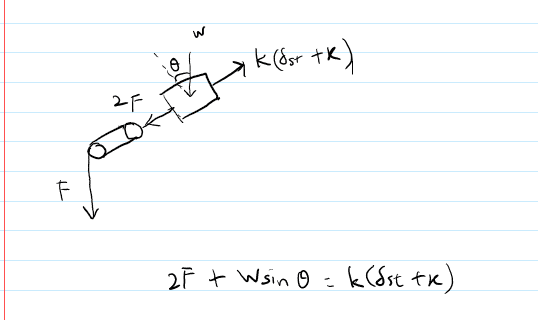To express the natural frequency ωₙ in terms of mass (m) and stiffness (k), one approach involves using Newton's laws and free body diagrams for each mass in a pulley system. The discussion highlights the importance of understanding the initial displacement, denoted as δₛₜ, and how it relates to the system's dynamics. A simpler method suggested is to utilize energy methods by introducing a generalized coordinate x to derive kinetic and potential energies. The natural frequency can be determined from the total energy equation, leading to the relationship ω² = k/μ, where μ represents the effective mass. Ultimately, both force equations and energy conservation can be employed to derive the desired expression for ωₙ.