How to solve a differential equation for a mass-spring oscillator?

[bolzano95]

Homework Statement

There is an mass-spring oscillator made of a spring with stiffness k and a block of mass m. The block is affected by a friction.
At the time $t=0s$ the block is pulled from the equilibrium position for $x=5cm$ in the right direction and released.
Derive and solve the equation for a displacement x, velocity v and power P.

Relevant Equations

II. Newton's Law

There is an mass-spring oscillator made of a spring with stiffness k and a block of mass m. The block is affected by a friction given by the equation:
$$F_f = -k_f N tanh(\frac{v}{v_c})$$
$k_f$ - friction coefficient
N - normal force
$v_c$ - velocity tolerance.

At the time $t=0s$ the block is pulled from the equilibrium position for $x=5cm$ in the right direction and released.
1. Derive the differential equation.
2. Solve it for a displacement x.
3. Solve it for a velocity v.
4. Solve it for the power loss P, because of the friction.

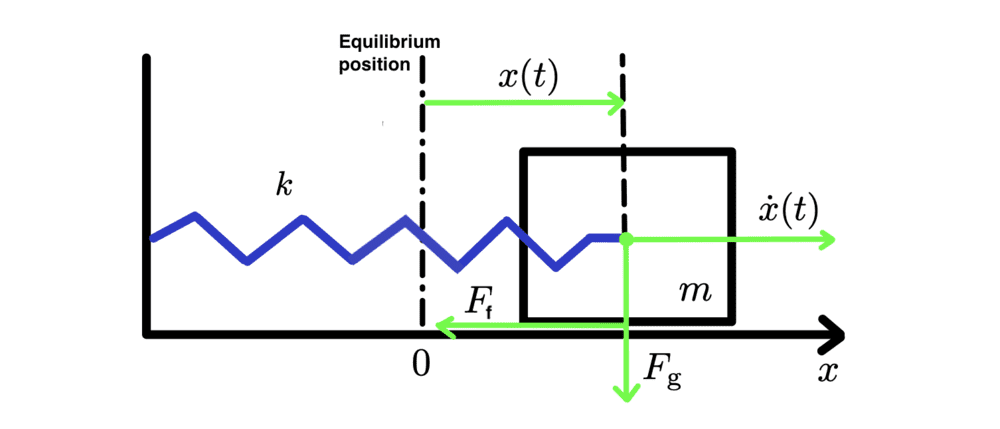
1. Deriving the necessary equation:
In the vertical direction: N=mg.
Because the only forces acting on the block in horizontal direction are the spring force and friction we can write:
$$-kx + k_f\, N\, tanh(\frac{\dot{x}}{v_c})=m\ddot{x}$$
$$m\ddot{x} - k_f\: mg\: tanh(\frac{\dot{x}}{v_c}) +kx=0$$

Here my solving stops, because I'm not sure how to implement the standard solution $x(t)= Ce^{\lambda t}$ because velocity is inside the function $tanh(\frac{\dot{x}}{v_c})$.

 

[TSny]

You are given a numerical value for the initial displacement. Are you given numerical values for any of the other parameters such as $k, k_f, v_c$ and $m$?

At first glance, the differential equation looks difficult to solve unless you can make a small amplitude approximation such that $\dot x$ is always much less than $v_c$.

 

[bolzano95]

You are given a numerical value for the initial displacement. Are you given numerical values for any of the other parameters such as $k, k_f, v_c$ and $m$?

At first glance, the differential equation looks difficult to solve unless you can make a small amplitude approximation such that $\dot x$ is always much less than $v_c$.

Oh yes, the initial conditions and parameters of the system given.

So there is no chance of solving this analytically, only numerically?