aawahab76
- 44
- 0
yes, my apology for you.Fredrik said:Yes, I said that they are. (Second sentence in #44).
yes, my apology for you.Fredrik said:Yes, I said that they are. (Second sentence in #44).
DaleSpam said:This is personal preference, but my feeling is exactly the opposite. I think that too much history is included in physics education to the detriment of learning a theory. E.g. Einstein's thought experiments only confused me and it wasn't until I found a more modern geometrical treatment that relativity finally "clicked" for me.
Now back to our problem.DaleSpam said:Yes.
aawahab76 said:Now back to our problem.
1- The event (1 sec, 10^100 m) (let us call from now on P) happened after the event (0,0) (let us call from now on O) in the x-frame.
2- So when the origin of the x'-frame passes through the origin of the x-frame, the observer in the origin of the x-frame is very sure that P did not happen yet.
3- However, for the x'-frame, P already happened.
4- the observer in the x'-frame can deliver a message to the observer in x-frame stating that and event P already happened at (t'≈-10^81 sec, x'≈10^100 m).
5- the observer in x-frame read that message quickly and deliver in his turn an argent message, by say light signals (so I am assuming that the two messages delivery, receiving, reading and reaction will last less than a second in the x-frame) telling the observer in the x'-frame that the event P at (1 sec, 10^100 m) did not happen. Just to have some action, P might instead of a flash of light be a deadly explosion.
Now before continuing, is there any problem in what I said above?
Because with respect to x'-frame, P is given by (t'≈-10^81 sec, x'≈10^100 m) while O (the event of meeting of the two observers) is (0',0') so t' for P is before t' for O. That what it seems to be.bobc2 said:Statement 4. How did the x'-frame observer know that the the event had happened?
aawahab76 said:Because with respect to x'-frame, P is given by (t'≈-10^81 sec, x'≈10^100 m) while O (the event of meeting of the two observers) is (0',0') so t' for P is before t' for O. That what it seems to be.
aawahab76 said:Because with respect to x'-frame, P is given by (t'≈-10^81 sec, x'≈10^100 m) while O (the event of meeting of the two observers) is (0',0') so t' for P is before t' for O. That what it seems to be.
Yes, the observer at x'=0 will not get the information about the event at (t',x') = (-10^81,10^100) until t' = 10^91, it will be far too late for him to deliver a message to the x-frame observer.aawahab76 said:4- the observer in the x'-frame can deliver a message to the observer in x-frame stating that and event P already happened at (t'≈-10^81 sec, x'≈10^100 m).
...
Now before continuing, is there any problem in what I said above?
Yes I agree with this and with what bobc2 said. So let us then and before any thing else answer this question: assume I am the observer in the x-frame. Now I build my frame using the usual method of rulers and synchronized clocks. When an event at P happens, how can I register its coordinates? Of course this question can be generalized to how can an observer register a particle path, too.DaleSpam said:Yes, the observer at x'=0 will not get the information about the event at (t',x') = (-10^81,10^100) until t' = 10^91, it will be far too late for him to deliver a message to the x-frame observer.
see post 22 above: https://www.physicsforums.com/showpost.php?p=3110316&postcount=22
aawahab76 said:Yes I agree with this and with what bobc2 said. So let us then and before any thing else answer this question: assume I am the observer in the x-frame. Now I build my frame using the usual method of rulers and synchronized clocks. When an event at P happens, how can I register its coordinates? Of course this question can be generalized to how can an observer register a particle path, too.
Well, you can assume that next to each clock is a camera recording local events in the neighborhood of that clock, and the feeds from each camera are being sent to the central observer at the speed of light. So the observer may not learn about a given event until long after it happens, but when he does learn about it he can just look at the clock and ruler-marking that were right next to the event when it happened to see what position and time coordinates should (retroactively) be assigned to the event.aawahab76 said:Yes I agree with this and with what bobc2 said. So let us then and before any thing else answer this question: assume I am the observer in the x-frame. Now I build my frame using the usual method of rulers and synchronized clocks. When an event at P happens, how can I register its coordinates? Of course this question can be generalized to how can an observer register a particle path, too.
JesseM said:Well, you can assume that next to each clock is a camera recording local events in the neighborhood of that clock, and the feeds from each camera are being sent to the central observer at the speed of light. So the observer may not learn about a given event until long after it happens, but when he does learn about it he can just look at the clock and ruler-marking that were right next to the event when it happened to see what position and time coordinates should (retroactively) be assigned to the event.
Beautiful efforts from all contributors. Now I can imagine the following physical processes and conditions that characterize our original problem. I will organize them in bullets and keep in mind that we are treating one dimensional problem.JesseM said:Well, you can assume that next to each clock is a camera recording local events in the neighborhood of that clock, and the feeds from each camera are being sent to the central observer at the speed of light. So the observer may not learn about a given event until long after it happens, but when he does learn about it he can just look at the clock and ruler-marking that were right next to the event when it happened to see what position and time coordinates should (retroactively) be assigned to the event.
I like JesseM's approach:aawahab76 said:Yes I agree with this and with what bobc2 said. So let us then and before any thing else answer this question: assume I am the observer in the x-frame. Now I build my frame using the usual method of rulers and synchronized clocks. When an event at P happens, how can I register its coordinates? Of course this question can be generalized to how can an observer register a particle path, too.
Equivalently you can use radar ranging techniques.JesseM said:Well, you can assume that next to each clock is a camera recording local events in the neighborhood of that clock, and the feeds from each camera are being sent to the central observer at the speed of light. So the observer may not learn about a given event until long after it happens, but when he does learn about it he can just look at the clock and ruler-marking that were right next to the event when it happened to see what position and time coordinates should (retroactively) be assigned to the event.
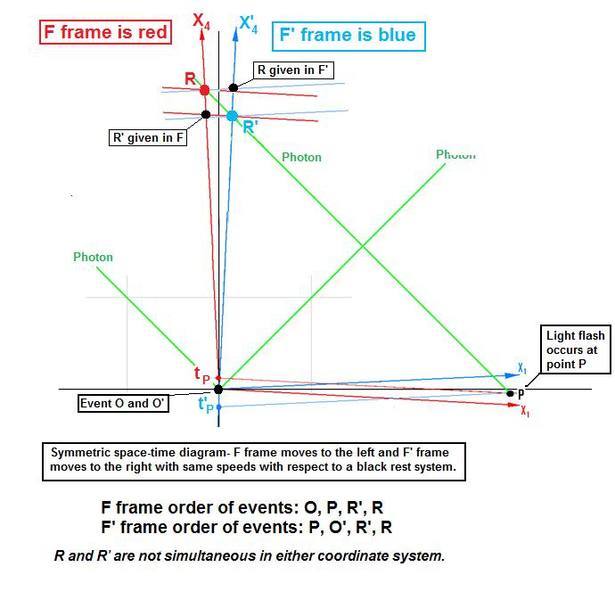
Thanks, I think graphs may seem more complicated at this point, but could you check using the Lorentz transformation.bobc2 said:aawahab76, I probably am answering a question that hasn't been asked again. However, I don't seem to get the same ordering of events as you've listed when I do the space-time diagram. This time I used a symmetric diagram in order to be sure that the scaling will be the same for both F and F'.
By the way, I have not used such small speeds as you wished, because it would require a much larger screen to achieve the required resolution. But, the basic relationships would not change. If you imagine rotating the axes so that they asymptotically approach the perpendiculare black coordinates, you will see that the points on the t and t' axes just get closer and closer together, so that the order of events are as they appear in my diagram.
My intention of the above list, to be completed below, is to find contradictory result or to grasp the physical sitiuation which is my aim from the begining.aawahab76 said:Beautiful efforts from all contributors. Now I can imagine the following physical processes and conditions that characterize our original problem. I will organize them in bullets and keep in mind that we are treating one dimensional problem.
1- An observer in the x-frame has built his frame with the usual rulers and synchronized clocks (by the known method of Poincare and Einstein) with coordinates (t,x). We call this observer and its frame F. I think it would be understood when F ( and similarly for F' below) means the frame or the observer (located at the origin of spatial coordinates).
2- The same has been done by the x'-frame observer with coordinates (t',x'). This is called F'. F' moves with the speed v=10^(-10) m/s with respect to F (so F moves with the speed -10^(-10) m/s with respect to F").
3- An event is an absolute physical process and is independent of coordinates (or frames). An event can be represented in coordinates given by the reading of the clock and the reading of the ruler located at the event. This is done separately by each observer using his or her coordinates.
4- F and F' agree to set their time coordinates such that the event of their meeting is given by (0,0) in F and by (0',0') by F'. (0,0) is named O, and (0',0') is named O'.
5- An event P happen at (t,x)=(1 sec, 10^100 m) in F and at (t',x') in F' ( that is in F, P happened after O). We assume that the event is a flash of light.
6- The Lorentz transformation gives the corresponding coordinates of P at F', that is (t'≈-10^81 sec, x'≈10^100 m).
7- F receives the light from P at the event R given in F by (10^100/(3*10^8)=3.3*10^92 sec, 0).
8- Using the Lorentz transformation, R is given in F' by (3.3*10^92 sec, -10^91 m).
9- F' receives the light from P at the event R' given by (≈-10^10^81+10^100/(3*10^8)≈3.3*10^92 sec, 0').
10- R' is given in F by using Lorentz transformation by (≈3.3*10^92 sec, ≈9.9*10^90 m).
11- In summary, in F we have the following events O, P, R and R’. Order of these events is O, P, and both R and R’ at the same time.
12- Similarly, in F’ we have O’, P, R’ and R. Their order is P, O’, and both R and R’ at the same time.
13- Thus, our original problem can be cast in the following threefold points:
i- how does O before P in F but P before O' in F' (notice that O' is the coordinate representation in F' of the same event O)?
ii- why does a very small relative speed lead to such a huge difference in time for the event P in F' relative to F?
iii- why the Lorentz transformation (LT) does not in general reduce to the Galilean transformation (GT) ( but I think this may not be true if we define the non-relativistic limit to be the limit when c goes to infinity in which case LT reduces in general to GT). Any way, this third point may not be of interest at this moment.
to be continued but please feel free to comment, correct .. etc.
aawahab76 said:My intention of the above list, to be completed below, is to find contradictory result or to grasp the physical sitiuation which is my aim from the begining.
aawahab76 said:My intention of the above list, to be completed below, is to find contradictory result or to grasp the physical sitiuation which is my aim from the begining.
The following is the exact calculation but the gamma factor which is very small was deleted and because it is a multiplicarive factor in all numbers below, it will not affect any equality result if it is thereDaleSpam said:R' and R are two events which are lightlike separated, therefore they cannot occur at the same time. You are just experiencing some roundoff error and you probably have to use an arbitrary precision math package and look at the 10th decimal place to see the difference. I haven't checked your numbers, but I provided some numbers in a previous post which you can use to compare.
i) because O and P are spacelike separated, as we have already discussed
ii) it is a small difference in time, as I said several times already
iii) it does reduce to the Galilean transformation in the limit as c -> infinity
aawahab76 said:The following is the exact calculation but the gamma factor which is very small was deleted and because it is a multiplicarive factor in all numbers below, it will not affect any equality result if it is there
- R is (10^100/(3*10^8)=((10/3)*10^92 sec, 0) in F so in F' it is ((10/3)*10^92 sec,-10^91 m)
- R' is (1-(1/3)*10^82+(1/3)*10^92-(0.03/3)*10^(-8), 0')=((1-10^(-10))(1+(1/3)*10^92) sec,0') in F' but in F is given by ((1-10^(-10))(1+(1/3)*10^92) sec, 3*10^(-2)*(1-10^(-10))(1+(1/3)*10^92))
So what you said is true. However, for the moment, this is not related to our problem as I stated it in the list above but I think I can add to the list
14- As measured by the corresponding frame, P happened in very different times, but at approximately the same spatial location and received in approximately the same time by each observer. I am not yet intending any physical interpretation of this observation, if it is correct.
Thanks and you are correct (in F, R time is 10 times that of R'). The new corrected list is:bobc2 said:aawahab76,
I don't think the signal from event P is received at approximately the same time by each observer. Now, R' as given in the F frame (refer to my sketch) is approximately R'--maybe that is what you are thinking.
These have all been answered. Are you unclear about the answers?aawahab76 said:i- how does O before P in F but P before O' in F' (notice that O' is the coordinate representation in F' of the same event O)?
ii- why does a very small relative speed lead to such a huge difference in time for the event P in F' relative to F?
iii- why the Lorentz transformation (LT) does not in general reduce to the Galilean transformation (GT) ( but I think this may not be true if we define the non-relativistic limit to be the limit when c goes to infinity in which case LT reduces in general to GT).
A side from point 3 which is now settled and can be omitted, the answers given for the first two points are the usual graph-LT equation method (I do not know a name for such method), a method which I believe does not satisfy our physical intuition (specially point 1). Notice that the graph-LT equation method is completely accepted and our discussion as I stressed more than once should not be concentrated on that very understood solution but should be directed toward a more physically clear one. Yes, at the end we may find our self forced to accept the graph-LT equation method in the lack of any physically appealing picture (as I believe we do in quantum mechanics in many of its non-intuitive concepts).DaleSpam said:These have all been answered. Are you unclear about the answers?
We call it the "geometric interpretation" or "Minkowski geometry". I personally find it very intuitive and satisfying.aawahab76 said:the answers given for the first two points are the usual graph-LT equation method (I do not know a name for such method), a method which I believe does not satisfy our physical intuition (specially point 1).
I gave you answers not involving graphs or the equations of the LT, but rather involving the fact that each observer uses their own set of rulers and synchronized clocks to assign position and time coordinates to events using local measurements, and that the method each observer uses to synchronize their own clocks ensures that each observer will measure the other observer's clocks to be out-of-sync, with the amount that two clocks are out-of-sync being greater the larger the distance between the clocks. Are you unconvinced that this physical method will provide coordinates that match those of the abstract Lorentz transformation? Or do you think this give an adequate physical picture of where the coordinates of the Lorentz transformation come from, but you think that this method of synchronizing clocks is problematic since it doesn't match your own physical intuition (not 'our' physical intuition, speak for yourself) that there must be some objective truth about which of two events happened first?aawahab76 said:A side from point 3 which is now settled and can be omitted, the answers given for the first two points are the usual graph-LT equation method (I do not know a name for such method), a method which I believe does not satisfy our physical intuition (specially point 1).
JesseM said:Do you also understand the meaning of Lorentz-invariance? As long as the equations of all the fundamental laws of physics (quantum field theory, for example), are Lorentz-invariant, that implies that it should be impossible in principle for any experiment to pick out a preferred inertial frame, the equations of the laws of physics will look the same when expressed in the coordinates of any inertial frame. This implies that no possible experiment could pick out a preferred definition of simultaneity, although as I said earlier you are free to adopt some sort of metaphysical belief that there is a "real truth" about which of a given pair of spacelike-separated events happened earlier (or if they 'really' happened simultaneously), as long as you acknowledge that this truth couldn't be discovered by any possible experiment your view won't conflict with relativity (but metaphysically I prefer eternalism to presentism, so I don't see the need for there to be any objective truth about which events are simultaneous and which aren't).
aawahab76 said:A side from point 3 which is now settled and can be omitted, the answers given for the first two points are the usual graph-LT equation method (I do not know a name for such method), a method which I believe does not satisfy our physical intuition (specially point 1). Notice that the graph-LT equation method is completely accepted and our discussion as I stressed more than once should not be concentrated on that very understood solution but should be directed toward a more physically clear one. Yes, at the end we may find our self forced to accept the graph-LT equation method in the lack of any physically appealing picture (as I believe we do in quantum mechanics in many of its non-intuitive concepts).
Yes every body may have a different viewpoint on the meaning of "physical intuition" and thus may find some statement physically intuitive and satisfying as you do with regard to our problem while others do not. This also explain why intuition is not a goal of a physical theory as it is more or less subjective (at least to some extent). However, scientists always try to think in terms of a "physical intuition" of some meaning. This I believe not to be of a philosophical nature but rather originate from the ability to describe nature in some cases in more than one way. Think of describing gravitational interaction in terms of "action at a distance" and in terms of "particle exchange". Particle exchange seems to be more intuitive but if nature can not be described but by the action at a distance, then let it be. Again here a scientist here or there will always be working to find the more "intuitive" picture.DaleSpam said:We call it the "geometric interpretation" or "Minkowski geometry". I personally find it very intuitive and satisfying.
If you don't find it intuitive then you need to understand that your physical intuition is not reliable and that satisfying it is not a requirement nor even a goal of a correct theory of physics.
Exactly. You should focus on understanding the objective math and experimental data, not the subjective intuition. Reversing the priority would be a mistake.aawahab76 said:Yes every body may have a different viewpoint on the meaning of "physical intuition" and thus may find some statement physically intuitive and satisfying as you do with regard to our problem while others do not. This also explain why intuition is not a goal of a physical theory as it is more or less subjective (at least to some extent).
Not really because you just used the essential structure behind the LT and graph to explain the same thing that equation and graph are doing (especially the definition of the simultaneity concept, they are all resulting from the same consistent structure of special relativity which I don not question here).JesseM said:I gave you answers not involving graphs or the equations of the LT, but rather involving the fact that each observer uses their own set of rulers and synchronized clocks to assign position and time coordinates to events using local measurements, and that the method each observer uses to synchronize their own clocks ensures that each observer will measure the other observer's clocks to be out-of-sync, with the amount that two clocks are out-of-sync being greater the larger the distance between the clocks. Are you unconvinced that this physical method will provide coordinates that match those of the abstract Lorentz transformation? Or do you think this give an adequate physical picture of where the coordinates of the Lorentz transformation come from, but you think that this method of synchronizing clocks is problematic since it doesn't match your own physical intuition (not 'our' physical intuition, speak for yourself) that there must be some objective truth about which of two events happened first?
Keep in mind that as a philosophical matter you are free to believe there is some "metaphysical truth" about simultaneity, so that there is one frame whose definition of simultaneity is "metaphysically correct" while others are "incorrect". But the Lorentz-invariance of the laws of physics implies that all physical experiments will give the same result in every frame, so no experiment can pick out a preferred frame or a preferred definition of simultaneity, thus even if some frame is "metaphysically preferred" and its judgments about the order of events are more "correct" than other frames', we could never discover which frame that is! This is why I asked in post #29 whether you understood the meaning of Lorentz-invariance, which you didn't answer:
I do not think so. Yes science must be built on experiment and objective concepts but who said that intuition is completely subjective (as I said in my comment). I think it is better to have an intuitive picture (what ever that means) rather than less intuitive one.DaleSpam said:Exactly. You should focus on understanding the objective math and experimental data, not the subjective intuition. Reversing the priority would be a mistake.
In your case, the relativity of simultaneity seems to go strongly against your intuition. Therefore your intuition needs to change. Familiarity with the math and the data can help that.
Your intuition is wrong, so why should we seek for a model which is intuitive to you? Your intuition needs to change, not the model.aawahab76 said:I do not think so. Yes science must be built on experiment and objective concepts but who said that intuition is completely subjective (as I said in my comment). I think it is better to have an intuitive picture (what ever that means) rather than less intuitive one.
My intuition is not necessarily wrong, it could be the other way round, that is the theory is wrong (but certainly I am not putting any theory to the test of intuition). However, that is neither our aim here nor that there is any thing to make us believe so.DaleSpam said:Your intuition is wrong, so why should we seek for a model which is intuitive to you? Your intuition needs to change, not the model.
How can a frame "know" anything? You're anthropomorphizing, only an individual with a brain (or some other information-processing system like a computer) at a distinct position in space can really be said to "know" about an event. If two observers meet at a single position, then either they are both inside the future light cone of an event or they're both outside the light cone, if they're inside then they both know about the event (and it happened at an earlier time-coordinate than their meeting in both frames), if their meeting happens outside the event's future light cone then they are both ignorant of it, even if in one observer's frame it happened at an earlier time coordinate than their meeting (in this case there is a spacelike separation between the event and their meeting, which is synonymous with the idea that their meeting is outside the future or past light cone of the event). Do you disagree with (or just doubt) any of this?aawahab76 said:My issue is that I am not yet convinced (I am again do not questio LT ... etc) that when the two observers (using two frames as discussed above) meet, one frame (F) does not yet know of an explosion (that is there is no point on F that registered the explosion because it needs another second to do so) that was already registered in the other frame (F").
Sure, in the frame where it happened earlier than the meeting, the synchronized clock at rest in that frame that was right next to the explosion as it happened (call it clock #1) showed an earlier reading than the synchronized clock at rest in the same frame (call it clock #2) that was next to the two observers at the moment they met. But the observer at rest in this frame will only learn about this later, when the signal from the camera next to clock #1 arrives at his own position (according to the scheme I outlined in [post=3114649]post 61[/post] which you seemed satisfied with). Here's the logic:aawahab76 said:This explosion is real and I believe it must have been recorded by the x-coordinates some time before the observers meet. I want to understand the missing logic in this last statement.
Yes, your intuition is necessarily wrong. And until you intuitively grasp the relativity of simultaneity it will continue to be wrong.aawahab76 said:My intuition is not necessarily wrong
JesseM said:How can a frame "know" anything? You're anthropomorphizing, only an individual with a brain (or some other information-processing system like a computer) at a distinct position in space can really be said to "know" about an event. If two observers meet at a single position, then either they are both inside the future light cone of an event or they're both outside the light cone, if they're inside then they both know about the event (and it happened at an earlier time-coordinate than their meeting in both frames), if their meeting happens outside the event's future light cone then they are both ignorant of it, even if in one observer's frame it happened at an earlier time coordinate than their meeting (in this case there is a spacelike separation between the event and their meeting, which is synonymous with the idea that their meeting is outside the future or past light cone of the event). Do you disagree with (or just doubt) any of this?
Sure, in the frame where it happened earlier than the meeting, the synchronized clock at rest in that frame that was right next to the explosion as it happened (call it clock #1) showed an earlier reading than the synchronized clock at rest in the same frame (call it clock #2) that was next to the two observers at the moment they met. But the observer at rest in this frame will only learn about this later, when the signal from the camera next to clock #1 arrives at his own position (according to the scheme I outlined in [post=3114649]post 61[/post] which you seemed satisfied with). Here's the logic:
1. In order for the two frames to disagree on the order of the two events (i.e. the event of the explosion and the event of the two observers meeting), there must be a spacelike interval between the events
2. If there is a spacelike interval between events, then neither event lies in the other event's future light cone, so no signal traveling at the speed of light or slower could travel from one event to the other event
3. Thus, regardless of which frame you use, the signal from the camera that was next to the explosion as it happened (and which shows the reading on the synchronized clock next to the explosion) will not have had time to reach either observer at the moment they first meet, so they will both be ignorant of it.
No, "simultaneous relative to an observer" is normally just a shorthand for "simultaneous in the observer's inertial rest frame", unless you're talking about the observer seeing the light from some pair of events simultaneously with their eyes (for example, if one star 200 light-years away in Earth's frame exploded in 1800, and another star 100 light-years away exploded in 1900, then on Earth we would see the light from these explosions simultaneously in 2000).aawahab76 said:Firstly, do you think that two events can be similtineuos with respect to a frame but not so with respect to a comoving observer in this frame? Does that make sense?
As long as I know, all such videos ... etc will try to simplify LT and graph rather than giving an "intuitive" physical picture. Just keep attention that we are concentrating on understanding if there is a physical contradiction (if that can be said) in the statemen that "P before O before and P' before O'", that is all.darkhorror said:If you want to see it in a more "physical" sense seems like you should just start with the basic that the speed of light is constant. Use math in a way where you come up with a scenario that your looking to understand. Use the speed of light and how it works twards time dilation, length contraction,... not just looking at the math but the math came to be. That may help so that you can see what's happening in a more physical way.
It also seems like there are already good descriptions and even videos of what you wondering about.
So at 1 sec in F, all space (as represented by x coordinate) is filled with events (being empty for example except at 10^100 m). However, space as it is is a physical structre that exist irrespictive of any coordinate and at this moment in F, P is being registered in x=10^100 m. But this space is already filling the F' space itself and as such it must be registered in the x' coordinte but after O,O' event as I can picture it (this is possibly where intuition come on). I am sure you may say that what I am saying is just with respect to a particuler frame that I find some how "intuitiv" but notice how we are now speaking about the totality of events (all x's) registered by a particuler frame at its global time coordinate rather than a single event.JesseM said:No, "simultaneous relative to an observer" is normally just a shorthand for "simultaneous in the observer's inertial rest frame", unless you're talking about the observer seeing the light from some pair of events simultaneously with their eyes (for example, if one star 200 light-years away in Earth's frame exploded in 1800, and another star 100 light-years away exploded in 1900, then on Earth we would see the light from these explosions simultaneously in 2000).
I don't understand what you mean by this. The statement "at this moment in F" is not one that's "irrespective of any coordinate", because talking about what's happening at different locations at a particular "moment" has no meaning outside the context of a particular coordinate system (unless you believe in some coordinate-independent notion of absolute simultaneity).aawahab76 said:So at 1 sec in F, all space (as represented by x coordinate) is filled with events (being empty for example except at 10^100 m). However, space as it is is a physical structre that exist irrespictive of any coordinate and at this moment in F, P is being registered in x=10^100 m.
Your phrasing is difficult to follow--when you say "it must be registered in the x' coordinate", what is the "it", is it event P? If so, by "registered in the x' coordinate" do you just mean P is assigned some coordinates in the primed frame?aawahab76 said:But this space is already filling the F' space itself and as such it must be registered in the x' coordinte but after O,O' event
"It" means all of space (in this case 1D space covering the whole x-axis in F and x'-axix in F').JesseM said:I don't understand what you mean by this. The statement "at this moment in F" is not one that's "irrespective of any coordinate", because talking about what's happening at different locations at a particular "moment" has no meaning outside the context of a particular coordinate system (unless you believe in some coordinate-independent notion of absolute simultaneity).
Your phrasing is difficult to follow--when you say "it must be registered in the x' coordinate", what is the "it", is it event P? If so, by "registered in the x' coordinate" do you just mean P is assigned some coordinates in the primed frame?
Sorry, but for the first paragraph (and excuse me for this but I do not know how to quote in the appropriate way, one may help here) yes why can't we define absolute simultaneity using t in F and t' in F' so event (t,x) is simultaneous with (t,y) for what ever x and y.JesseM said:I don't understand what you mean by this. The statement "at this moment in F" is not one that's "irrespective of any coordinate", because talking about what's happening at different locations at a particular "moment" has no meaning outside the context of a particular coordinate system (unless you believe in some coordinate-independent notion of absolute simultaneity).
Your phrasing is difficult to follow--when you say "it must be registered in the x' coordinate", what is the "it", is it event P? If so, by "registered in the x' coordinate" do you just mean P is assigned some coordinates in the primed frame?
aawahab76 said:Sorry, but for the first paragraph (and excuse me for this but I do not know how to quote in the appropriate way, one may help here) yes why can't we define absolute simultaneity using t in F and t' in F" so event (t,x) is simultaneous with (t,y) for what ever x and y.
Again this isn't clear, as darkhorror said you don't seem to mention the t' coordinates of either event, and how is "using t in and t' in F' " supposed to give an absolute definition of simultaneity? "Absolute" here means something that all observers can agree on, but obviously a pair of events that have the same t-coordinate have different t'-coordinates and vice versa.aawahab76 said:Sorry, but for the first paragraph (and excuse me for this but I do not know how to quote in the appropriate way, one may help here) yes why can't we define absolute simultaneity using t in F and t' in F' so event (t,x) is simultaneous with (t,y) for what ever x and y.
t' is the time coordinate in F' and F'' is a mistake I corrected above, it is F'. Thanks darkhorrordarkhorror said:where do you use t' and F"?
That was my bad composition , I mean the following:darkhorror said:I wasn't actually talking about the " vs ', the naming of them doesn't really matter. But where do you mention t' and F' after you say that there is that frame? you only mention (t,x) and (t,y).
Because "absolute simultaneity" means a single truth about simultaneity that is the same for all observers. Two events that are simultaneous in F will not be simultaneous when their coordinates are translated into F', and vice versa.aawahab76 said:That was my bad composition , I mean the following:
why can't we define absolute simultaneity using t in F and t' in F' so:
1- in F, event (t,x) is simultaneous with (t,y) for what ever x and y
2- in F', event (t',x') is simultaneous with (t',y') for what ever x' and y'?