- #71
m.starkov
- 35
- 0
Please take a look
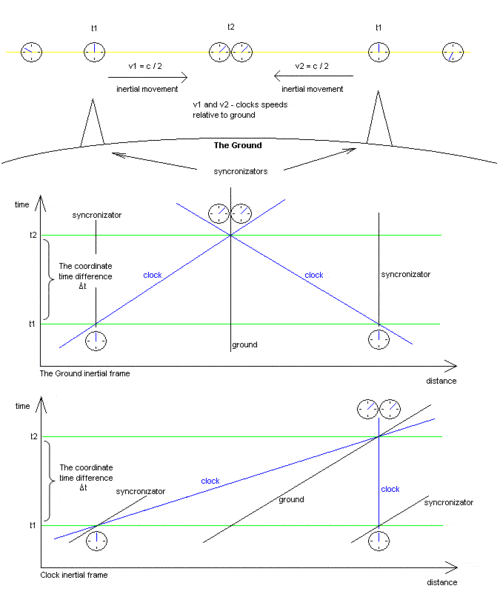
The coordinate time difference (Δt) is the same for both clocks in both cases.
So why not use the clock inertial frame for calculations? Can we?
The coordinate time difference (Δt) is the same for both clocks in both cases.
So why not use the clock inertial frame for calculations? Can we?
Last edited: