Is Velocity Addition in Special Relativity Contradictory?

[Ken Natton]

Well Ich, all I can say then is that you and I seem to have been at cross purposes. I always understood that there may be some serious practicality issues with the situation we were describing. Believe me, I am an engineer. I’m a software engineer not a mechanical engineer, but I served a generic engineering apprenticeship and I work with mechanical engineers and process engineers. I do have some grasp of the practicalities. In point of fact, if you built your track strong enough, it might well be the drive that would overload and fail first. But for certain, if you put undue tension into the system, something somewhere would eventually have to give. As I have said previously, that applies just as well at 10mph as it does at 0.45c.

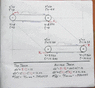
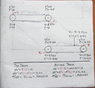
But, taking the very risky step of speaking for them, in my understanding at least, that was not the objection Calebholiday or Austin0 were belabouring. Their case, as I understood it, did centre around the idea that the difference in relative velocities of the upper and lower tracks, by relativity theory, meant differences in length contractions that would put impossible strains into the system. My case was only that that constituted a misunderstanding of what length contraction is. If I am right about that then perhaps the accurate description of exactly what length contraction is that you and I have agreed upon might just clear up the issue.

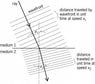
But my broader case, that I cannot prove with nothing but logic, that my guess is would require some differential calculus of which I am not capable, is that it can be shown mathematically that the apparent differences in length contractions to the ground observer are balanced out by the time dilations and velocity differences such that there is no mystery to the ground observer as to why the track is able to keep going. I understand that you offered a detailed solution to that based on the number of segments passing a given point, but I think that it can be done purely algebraically showing how the velocity differences, length contractions and time dilations balance out.

 

[Ich]

Their case, as I understood it, did centre around the idea that the difference in relative velocities of the upper and lower tracks, by relativity theory, meant differences in length contractions that would put impossible strains into the system.

Maybe.

My case was only that that constituted a misunderstanding of what length contraction is. If I am right about that then perhaps the accurate description of exactly what length contraction is that you and I have agreed upon might just clear up the issue.

You're right.

I understand that you offered a detailed solution to that based on the number of segments passing a given point, but I think that it can be done purely algebraically showing how the velocity differences, length contractions and time dilations balance out.

My solution was aimed at arguments that supposedly show that the upper track has to go at double tank speed. Do you want to do it in symbols instead of numbers, or what exactly do you want to show?

 

[Ken Natton]

Okay, on that point I agree with you entirely Ich, and quite understand your frustration and that of the other serious contributors to this thread. Suggestions that the top track moves at 0.9c are based on nothing but pigheadedness. For a mathematical proof of that point, we need do more than refer them to a certain paper published in 1905 by one Albert Einstein called On the Electro… you know where I am going with that. The point is that paper does include a mathematical derivation of the velocity addition formula that proves that the top track moves at the value first identified on this thread by you. If they want to disagree with that then they have some serious explaining to do about the constant value of the speed of light in all reference frames, which is an experimentally proven fact – real experiment not thought experiment.

Leaving aside any other objections raised by any other contributors to this thread perhaps you and I can agree this: Relative to what we have been calling the ground observer, the top track moves at a significantly different velocity to the bottom track. By relativity theory, that means that the length contraction of the top track is significantly different to the length contraction of the bottom track. Considering nothing else, that might appear to be anomalous. Simple logic would tell you that for the continuous smooth feed of the track around the whole system, the top track must travel the same distance in the same time going forward as the bottom track does going rearwards. Or perhaps I would be better to phrase it as that the top track travels the same distance in spacetime going forward as the bottom track does going rearward.

If we do agree on that, then it seems to me that it should be possible to demonstrate mathematically that the apparent difference in length contraction is balanced by the corresponding differences in velocity and in time dilation. I’m not tremendously concerned about whether that is done algebraically or with some sample actual numbers, but clearly the algebraic solution is the more generic. If that proof was offered, I could walk away from this thread contented and leave those who wish to disagree with it to disappear into their own logical fallacies.

 

[Ich]

Simple logic would tell you that for the continuous smooth feed of the track around the whole system, the top track must travel the same distance in the same time going forward as the bottom track does going rearwards. [...]
If we do agree on that, then it seems to me that it should be possible to demonstrate mathematically that the apparent difference in length contraction is balanced by the corresponding differences in velocity and in time dilation. I’m not tremendously concerned about whether that is done algebraically or with some sample actual numbers, but clearly the algebraic solution is the more generic. If that proof was offered, I could walk away from this thread contented and leave those who wish to disagree with it to disappear into their own logical fallacies.

Well, I think I've given that proof in https://www.physicsforums.com/showpost.php?p=2810402&postcount=32".

Time dilation is not an issue, as we're working in the ground frame only.
"u" is the speed of the tank.
We have:
upper track:
speed: $v=\frac{2u}{1+u^2}$
Length contraction factor: $1/\gamma = \sqrt{1-v^2}$
lower track:
speed v=0
Length contraction factor: 1

Now through the middle plane - which is moving forward with velocity u - you transport a track length of
$$\Delta t \, (v-u),$$
which equals a proper track length (i.e. length contraction taken into account) of
$$\Delta t \, \gamma (v-u).$$
This is -0.45 for the lower track.
It needs a bit of algebra to show that it's +0.45 for the upper track, which proves that in order to work properly, the speed of the upper track must be the value that you get from velocity addition.
Maybe you want to try the calculation yourself, you have all the formulas you need.

 

[Ken Natton]

Nope, Ich. I can’t do it. You said, a little dismissively, ‘you have all the formulae you need’. And I suppose that I do. But then I had all the formulae I needed all along, all of these formulae are in the public domain. I suppose it’s not the formulae that I am missing. I can see that a question might legitimately be raised as to exactly why I am making this post. To answer that question I might risk accusations of arrogance and claim that, on a thread that has experienced a bit of misunderstanding and some misalignment between questions asked and answers supplied, I am going to attempt to bring a little clarity; clarity of statement of the problem at least, because I can’t provide any kind of statement about the solution. The follow up question that I might then be asked is ‘clarity for whom exactly?’ And the truthful answer to that may well be ‘for no-one but myself’.

A clear statement of those formulae does add something to the clarification of the argument, so let’s just quickly state them. I have taken on board your assertion that setting c = 1 and thus stating all other velocities as a proportion of c, together with judicious use of the Lorentz factor, does have a tendency to simplify the formulae. So, in that vein:

Lorentz Factor:

$$\gamma=\frac{1}{\sqrt{1-v^2}}$$​

Velocity Addition:

$$s=\frac{v+u}{1+vu }$$​

Length Contraction:

$$x’=\frac{x}{\gamma}$$​

Time Dilation:

$$t’=\gamma t$$​

In the velocity addition formula, v is the velocity of the first body relative to the stationary frame, u is the velocity of the second body relative to the first and s is the velocity of the second body relative to the stationary frame.

The reason that stating these formulae provides clarity to the argument is that it enables us to classify exactly what the argument is. The derivations of these formulae are also openly available. The question of their accuracy is nothing specific to the tank track problem, and to question them is actually to question relativity theory, which in point of fact is actually against forum rules. Not that I am trying to hide behind that fact, but it is clear that a questioning of these formulae is an argument of a completely different nature. If the basic formulae are accepted, then all we are trying to achieve is an understanding of how they help to resolve the tank track problem.

My first attempt to resolve it by making use of these formulae – in post #27 – crashed in a snotty heap because of whatever it is that I am missing. Clearly, I am still missing something, but I have made some progress since then.

1. The different length contractions
I was focused on the difference in length contraction between the bottom track and the top track. There is actually a third length contraction involved, that between the front and rear wheels. I know others are going to say we already said that, but it didn’t penetrate at the time and now that I get it, I see a value in the clear statement of the length contraction differences:

If we state clearly that:

$$l$$ = the uncontracted length under discussion
$$l_w$$ = the wheel base, the distance from the centreline of the rear wheel to the centreline of the front wheel
$$l_t$$ = the length of the top track – the length of linear forward travel
$$l_b$$ = the length of the bottom track – the length of linear rearward travel

then, when the tank is stationary in front of us in the ground frame, clearly
$$l = l_w = l_t = l_b$$.

But when the tank is traveling at speed
$$l_w = \frac{l}{\gamma}$$
$$l_t = l {\times} \sqrt {1-s^2}$$ and
$$l_b = l$$

To put some values on it in our example of $$v = 0.45c$$,
$$l_w = 0.893l$$
$$l_t = 0.663l$$ and
$$l_b = l$$

Now it can be seen that apparently, the top track is hopelessly stretched over the wheel base and the bottom track is hopelessly loose. You explained this by taking advantage of the fact that tank tracks are usually segmented and stated that the segments, themselves length contracted, are more densely packed at the top, and uncontracted, are spaced further apart at the bottom. But the segmentation is a convenience and not really an explanation of the point. Perhaps this is not a tank track at all. Perhaps this is a continuous fabric conveyor belt stretched over two wheels, attached to the side of a body that has gained its velocity by some other means. The problem is the same. But my contention is that the conveyor belt is not really stretched at the top and hanging loose at the bottom. All we are really talking about is differences of deflection in spacetime between the conveyor top, the wheel base and the conveyor bottom relative to the ground frame.

You and I can both easily conceive a solution for Calebholiday’s design engineers. Obviously, real tank tracks actually have an arrangement of multiple wheels, and it would not be so difficult to have an arrangement that included some spring loaded tensioning wheels that could move around as required to maintain a constant tension throughout the system. But I am still not convinced that such an arrangement is really necessary, or that the differences in perception of the ground observer and the observer on board the tank are adequately explained by such a solution.

2. Distance traveled by the top track.
This is perhaps an even more basic point, but is something I have only realized in trying to work it out this time. The forward distance traveled by the top track at the speed calculated using the velocity addition formula is not just the appropriately contracted distance between the wheels. While the top track is traveling that distance, the tank itself is also traveling forward, thus the distance covered by any point on the top track is the appropriately contracted distance between the wheels, plus the appropriately contracted distance traveled by the tank in the time taken for that point to get from the rear wheel to the front wheel.

3. The equivalence to be proven
I was expecting to be able to show that velocities, distances and times balanced out in themselves. But they do not, so clearly that is not what is equivalent. My next thought was that it would be spacetime distance that was equivalent. So having arrived at values for velocity, length and time for each of the three cases, I envisaged plugging them into the good old Minkowski formula to find the distances in spacetime. But I can’t make that work either.

I know you say that you proved it in post #32. What you proved is that the number of segments per second gong forward are the same as the number of segments per second going rearward. I would have to stand with Austin0 and Calebholiday in saying that is not really a resolution of the apparent discrepancies of length and time.

In any case, I can anticipate that your patience has been exhausted. If so, let this post hang in the air for anyone else who cares to prod me in the direction of the solution I seek.

 

[Fredrik]

So in this case the geometry and mechanics would seem to indicate twice the distance covered and hence twice the velocity i.e. 0.9c

So it would appear that in the light of simultaneity you may have been right all along.

No, he wasn't. The correct answer has been posted many times, and I posted a proof that a topside speed of 0.9 leads to a logical inconsistency. This discussion should have been over a long time ago.

 

[yossell]

Ken,

I'm interested. But I think: whatever the wheel's made of, if, in the tank frame, the guy in the tank puts little dots at equal spaces around the wheel, then from the stationary frame, because of relativity of simultaneity and contraction effects, these dots will not be equally spaced around the tank (in stationary frame), but will be more densely packed along the top than at the bottom.

But when you talk of hopelessly loose and stretched,are you really just talking about deformation of length or is your worry the thought that there are asymmetric *tensions* in the tank, so that it's an actually an issue about forces? For instance: the top close to splitting like a rubber band; the bottom close to wobbling off like a loose tire? Spin too fast, and the top will come flying apart while the bottom will hold. But how could there be such an asymmetry? After all, the tank doesn't really have to be traveling on the ground - we could just imagine a suspended track whirring around, and imagine how things look from an observer who moves with the same velocity as the lower track. Now, in this scenario, from the tank's point of view, everything is balanced between top and bottom track?

To be honest, this has concerned me too - and the analysis of the forces at play in the tire is going to be delicate. But remember: there are no genuinely rigid rods SR. Quite literally, any material must `slooshes' around to a degree when there is acceleration: this is just a result of the fact that forces take time to propogate; moreover, the track is not like a rubber band, stretched tight and unable to move: its parts are always moving, and responding to the forces applied at the wheels, and whatever attractive forces keep the parts of the tread together.

In short, it's one thing to talk about length contraction, it's another thing to talk about tension; the analysis of the latter seems very complex to me - too complex to make me see that there is a problematic asymmetry of tension in the track in the moving frame.

It would be interesting to see a full resolution of the issue of forces from the two points of view - but for this there would probably have to be a lot more detail about the mechanisms involved in turning the track, in keeping the tension of the track great enough to keep its basic shape, and the forces in the track that keep it together.

In part, this complexity is why I've always tried to press people to be clear about exactly what they take the problem to be. I still don't see a clear formulation of the concrete worry.

But I think the attempt to do is useful

 

[Ken Natton]

Actually yossell, perhaps you have got as close to a resolution as we are going to get. (Now that I’ve praised you, could you call the lawyers off for that time when I expressed a preference for matheinste’s post?) In the light of another couple of threads recently started by Calebholiday, my doubts about his true agenda have started to grow. But it is clear, in this problem, he did offer a genuinely interesting, and as you suggest, useful poser. Useful in the sense that pondering it does tend to improve understanding. The thing is that it is, of course, at best naïve and at worst stupid to suggest that the problem presents any kind of undermining of relativity theory. What it perhaps demonstrates is that when we blithely talk about these concepts of length contraction and time dilation, they actually represent a reality that is a good deal more complex than we might at first realize. That is not intended to daunt anyone in the quest to understand better. I don’t agree with those who contend that relativity theory is an irrelevance to the lives of most people. I never expect to need, in a purely utilitarian way, any knowledge or understanding of relativity theory. That doesn’t mean that there is no value in trying to understand.

 

[Ich]

I know you say that you proved it in post #32. What you proved is that the number of segments per second gong forward are the same as the number of segments per second going rearward.

Yes, that's what I intended to prove. Because it shows that the "2v-claim" - which seems so reasonable - would actually lead to breaking the tracks, while velocity addition preserves them. The proof is relatively simple, as neither the stretching of the tracks nor simultaneity are relevant.

You said, a little dismissively, ‘you have all the formulae you need’.

That was not meant dismissively, it was meant to say that I posted all the formulas you need to follow the proof. You don't have to look elsewhere.

Then there's the issue of different track lengths (top vs bottom). Austin0 claimed this as evidence for undue stresses in the ground frame, without further thoughts or calculations. I dismissed that "evidence" claiming that he forgot the relativity of simultaneity.

Your example (which I understand now for the first time - if at all) is basically the same. Its resolution depends on physical stretching, lorentz contraction, and relativity of simultaneity, so it's necessarily complicated. I did not expect you to solve it.

First, the stretching of the track, in the tank frame:
I'm asking for the rest length of the track.
We have in the tank frame a length 2*l (top+bottom). But this is made up of Lorentz-contracted track.
If the contracted track has a length of 2*l, its rest length must be $2 l /0.893 = 2.24 l$.
So either the track has a length of 2.24l from the beginning (a very loose fit), or it gets stretched to this rest length during spin-up.

Now in the ground frame:
The top track is .893l long in that frame, and is made up of contracted track with a factor of 0.663. So the rest length of the upper track is $0.893 l/0.6632 = 1.347 l$
The bottom track is also .893l long in that frame, but it is not contracted at all. So its rest length is $0.893 l$.

Consistency check: the sum of both rest lengths is still 2.24l. Of course, there is no difference if we look at the same situation in different frames.

Now, does the result mean that the top track is severely stretched, while the bottom track is compressed?
No. Here's the appearance of Relativity of Simultaneity:
In the tank frame, at the rear wheel, there's track going from bottom to top at a constant rate. The rate in terms of contracted track is v, in terms of track rest length it is therefore $\gamma v = 1.12 v$.
The same amount goes down at the front wheel.
Everything is balanced.

In the ground frame, however, with its simultaneity convention, we see the rear wheel at a later time than the front wheel. It is, so to speak, $\Delta t =\gamma l_w v = l v =0.45 l$ older (tank time) than the front wheel.
In that tank time, a track rest length of $dl=1.12 v \Delta t = 1.12 v^2 = 0.227 l$ went up.
That means, instead of the equilibrium amount of 1.12l we see 1.12+.227=1.347 track rest length at the top, and 1.12-.227 = 0.893 at the bottom.
Not because there's additional stress, it's because we use a different simultaneity in the ground frame, where we measure the track at the rear wheel at a later (tank) time, where some of it already went up that did not come down at the front wheel.

I think it's fair to say that this is complicated stuff. And if I say that a newcomer has exactly zero chance of getting such things right, that's neither arrogance nor ad hominem, it's how it is.

 

[Ken Natton]

Superb Ich, absolutely superb. You have put your finger right on the very point I was missing. I had made no allowance at all for the relativity of simultaneity. And it makes immediate sense to me. In my attempts to play with sample numbers I had found, of course, that with a relatively short wheel base, my time values were all tiny fractions of a second. To get the times to something easier to deal with, I had to set the wheel base to 1 Gm. The point I am making is that, to keep the wheel base short enough that the effects of the relativity of simultaneity are minimal, the apparent length and time discrepancies are also negligible. As you increase the wheel base to a point where the discrepancies seem to be a concern, the effects of the relativity of simultaneity become significant. That was where the balance I sought lay.

Of course, I had to read your post two or three times before I stated to get it, but I am sure that I do get it. The proof, of course, would be that I can go away without your further help and put the numbers into my Excel spreadsheet for myself and find the balance myself.

In any case, I, at least, am resolved. I have closure. The only thing I need to figure out now is what the goodness I’m going to put on my time sheet!

 

[Austin0]

I think you misunderstand the point yossell is making. As far as I can see, unless I've missed it, nobody in this thread has given any reason for the 0.9c velocity in the ground frame that amounts to much more than "it must be", which is no good reason at all. The people who mistakenly believe this to be true need to sit down and think about it and produce a detailed step-by-step proof, then the rest of us can examine the "proof" to find out where the error is.

In the extremely unlikely event that your "proof" has no error, you will go down in history as the person who disproved relativity.

Hi DrGreg I thought I would take a shot at providing a reason .
I hope you can analyze it for error.

Attached drawing.

Tank:wheelbase length 10 ls in rest frame.

Starting the velocity test from the marked track points at the top point of the rear wheel (T₀)

and the bottom point of the front wheel (B₀).

Ground frame: x=o, t=0 , x'=0,t'=0 at rear wheel center

x= 8.930, t=0, x'=10, t'= (-4.5) at front wheel center.

At the point where the top track marked point is coincident with the top of the front wheel (T₁)and the bottom marked point is coincident with the rear wheel center (B₁) the coordinates are:

x=17.860 ,t=19.844 , x'=10 , t'=13.22 at the front wheel ...and

x= 8.930 , t=19.844 , x'=0 ,t'= 17.720 at the rear wheel.
_____________________________________________________________________________

TOP TRACK:

dx' = (T₁)- (T₀)=10

dt' =t'(T₁)-t'(T₀)= 13.22

v=dx'/dt' =10/13.22= .756429

BOTTOM TRACK:

dx'=(B₁) - (B₀) = abs(-10) =10

dt'= t'(B₁) - t' (B₀) = 22.22

dx'/dt'=10/22.22 =.450045

These figures were derived completely from fundamental priciples applied solely within the ground frame as specified by the original parameters.

The final velocity for the top track as measured in the tank frame is .756429 c

The velocity returned by the Addition of velocities function for (.9 +.45) is .75630 c

I did not do a simultaneity workup from the tank frame as I have confidence in the consistency of SR
and know that both frames must agree on these events.

SO my questions to you:

1) Is the above correct in its applications and results?

2) If there is no error , in your qualified opinion is this sufficient reason to consider the correct solution to be .9 c for the top track in the ground frame??

3) Can you think of any conditions that would be consistent with these events and still justify a measurement of .45 for the top in the tank frame?

In any case there are still interesting, unresolved questions regarding contraction and physics in this scenario.

Thanks PS I never entertained the idea that this question contained the seeds for a "disproof" of SR and frankly do not understand why anyone would think so.?

 

[JesseM]

Hi DrGreg I thought I would take a shot at providing a reason .
I hope you can analyze it for error.

Attached drawing.

Tank:wheelbase length 10 ls in rest frame.

Starting the velocity test from the marked track points at the top point of the rear wheel (T₀)

and the bottom point of the front wheel (B₀).

Ground frame: x=o, t=0 , x'=0,t'=0 at rear wheel center

x= 8.930, t=0, x'=10, t'= (-4.5) at front wheel center.

At the point where the top track marked point is coincident with the top of the front wheel (T₁)and the bottom marked point is coincident with the rear wheel center (B₁) the coordinates are:

x=17.860 ,t=19.844 , x'=10 , t'=13.22 at the front wheel ...and

x= 8.930 , t=19.844 , x'=0 ,t'= 17.720 at the rear wheel.
_____________________________________________________________________________

TOP TRACK:

dx' = (T₁)- (T₀)=10

dt' =t'(T₁)-t'(T₀)= 13.22

v=dx'/dt' =10/13.22= .756429

BOTTOM TRACK:

dx'=(B₁) - (B₀) = abs(-10) =10

dt'= t'(B₁) - t' (B₀) = 22.22

dx'/dt'=10/22.22 =.450045

These figures were derived completely from fundamental priciples applied solely within the ground frame as specified by the original parameters.

The final velocity for the top track as measured in the tank frame is .756429 c

Numbers look good, although the final velocity for the top track is slightly off, if we include more significant figures we find:

Relativistic gamma between ground frame and tank frame: 1/sqrt(1 - 0.45^2) = 1.11978502191171

Length of tank in ground frame = 10/gamma = 8.93028554974588 light-seconds

Time for tank to move exactly one full length in ground frame, so back wheel is at exactly the point the front wheel used to be: 8.93028554974588 ls/0.45c = 19.8450789994353 s

Position of front wheel after tank has moved one full length in ground frame, assuming back wheel was at x=0 at the start: x = 2*8.93028554974588 ls = 17.8605710994918 ls

So, if the marked point on the top track starts at the position of the back wheel, and by the time the tank has moved one full length it's at the position of the front wheel, then in the ground frame dx/dt for the marked point is (2*8.93028554974588)/(8.93028554974588/0.45) = 2*0.45 = 0.9 light-seconds/second.

If we know the coordinates where the top track marked point is at the front wheel are x=17.8605710994918, t=19.8450789994353 in the ground frame, then in the tank frame this translates to x'=10 and t'=1.11978502191171*(19.8450789994353 - 0.45*17.8605710994918)=13.2222222..., so the velocity of the top track marked point in the tank frame must be 10 ls/13.22222... s = (990/99)*c / (1309/99) = 990c/1309 = 90c/119 = 0.75630c, exactly equal to what you get below:

The velocity returned by the Addition of velocities function for (.9 +.45) is .75630 c

Since the top track marked point is moving at 0.9c in the ground frame, while in the tank frame the ground is moving at -0.45c, if you want to figure out the velocity of the marked point in the tank frame you have to plug in -0.45c in the velocity addition formula rather than +0.45c, which I assume is what you actually did since (0.9c - 0.45c)/(1 + (0.9c)*(-0.45c)/c^2) = 0.45c/0.595 = 90*0.005c/119*0.005 = 90c/119 = 0.75630c.

I think the confusion here may be that some people are thinking that if someone says a point on the top track is moving at 0.9c in the ground frame for a tank moving at 0.45c in that frame, they think this was obtained by assuming the point on the top track moved at 0.45c in the tank frame and then adding this to the velocity of the whole tank in the ground frame, which would be an incorrect addition of velocities in relativity. But in reality, when you understand that the point on the top track actually moves at 0.75630 in the tank frame, then you can see it makes sense that it'd move at 0.9c in the ground frame according to the relativistic velocity addition formula, since (0.45c + 0.75630c)/(1 + 0.45*0.75630) = 1.2063c/1.340335 = 0.9c.

Of course, all of these numbers are based on one key assumption made in your diagram: that the time for the marked point on the top track to go from the back wheel to the front wheel is the same as the time for the marked point on the bottom track to go from the front wheel to the back wheel, as seen in the ground frame! This doesn't necessarily have to be the case--you could equally well assume that in the tank frame the time for each marked point to go from one wheel to another is the same in both cases, since it can't be true in both frames (unlike in Newtonian physics where the times could be equal in all frames). So it really depends on your assumptions about how this fantasy tank moving at relativistic speeds actually works, whether in the tank frame the material is more bunched up on one top track and more stretched out on the other track (which would be true under your assumptions), or whether in the tank frame the material is equally stretched in both frames (which would be true if there were equal times in the tank frame for each spot to go from one wheel to another).

 

[Ich]

So it really depends on your assumptions about how this fantasy tank moving at relativistic speeds actually works, whether in the tank frame the material is more bunched up on one top track and more stretched out on the other track (which would be true under your assumptions), or whether in the tank frame the material is equally stretched in both frames (which would be true if there were equal times in the tank frame for each spot to go from one wheel to another).

No, you got this wrong. With Austin0's "fundamental priciples" the tank doesn't work at all, because the track gets infinitely wound up on the front wheel. This is not a matter of taste.

 

[JesseM]

No, you got this wrong. With Austin0's "fundamental priciples" the tank doesn't work at all, because the track gets infinitely wound up on the front wheel. This is not a matter of taste.

Not true, the idea that the track moves faster on top than on the bottom doesn't imply it gets progressively more bunched up as time goes on, any more than the fact that light moves slower through a medium than outside means that the wave peaks are more bunched up on one side of the medium than the other. See the following pair of images illustrating refraction in a medium that slows down light waves that travel through it, from this page and this one:

In Austin0's example, the tank is 10 light-seconds long in its own frame, and any point on the track moves at 0.45c when it's on the bottom, and at 0.75630c when it's on the top. So, consider two dots painted on the track which are 0.45 light-second apart when they're on the bottom. As in his example, the back wheel is at x'=0 at time t'=0, and let's assume that when a dot on the bottom track reaches the back wheel it switches to the top top track quasi-instantaneously. So, assume that at t'=0, dot A is at x'=0 and about to switch from the bottom track to the top track, and dot B is at x'=0.45. So dot B continues to move at 0.45c for 1 second in this frame, after which it's moved in the -x' direction a distance of (1 second)*(0.45c) = 0.45 light-seconds, so at t'=1 dot B is at x'=0. Meanwhile dot A has been moving at 0.75630c on the top track for this period, so at t'=1 dot A is at position x'=0.75630 light-seconds. And at t'=1 dot B switches from the bottom track to the top track, after which they both move at the same speed on the top track for a while, so while they're both on the top track they maintain a separation of 0.75630 light-seconds.

At t'=13.222... seconds, dot A has moved a distance of (13.222...)*(0.75630c) = 10 light-seconds from its position at t'=0, so it must now be at position x'=10, where it switches quasi-instantaneously back to the bottom track. Since the distance between A and B is always 0.75630 ls on the top track, at t'=13.222... dot B must be at x'=10 - 0.75630 = 9.2464 l.s. 1 second later at t'=14.222..., dot B will have moved an additional distance of (1 second)*(0.75630c) = 0.75630 ls, so that will be the moment that dot B reaches x'=10. Meanwhile dot A has been on the bottom track since t'=13.222... moving at 0.45c in the -x direction, so at t'=14.222... dot A is at x'=10 - (1 second)*(0.45c) = 9.55 light-seconds. And this is the time that dot B is at x'=10 and switches quasi-instantaneously back down to the bottom track, so if at t'=14.222... dot A is on the bottom track at x'=9.55 ls while dot B is on the bottom track at x'=10 ls, then at this moment both dot A and dot B are on the bottom track with a separation of 10-9.55=0.45 ls, which was their original separation before either of them switched to the top track. They'll continue to maintain this separation of 0.45 ls while both are on the bottom track until dot A reaches the back wheel and switches to the top track again, at which point we're back to the situation at the beginning. It's a stable cycle, whenever both dots are on the bottom track their separation is always 0.45 ls, and whenever both dots are on the top track their separation is always 0.75630 ls.

 

[Austin0]

Numbers look good, although the final velocity for the top track is slightly off, if we include more significant figures we find:

Relativistic gamma between ground frame and tank frame: 1/sqrt(1 - 0.45^2) = 1.11978502191171

Length of tank in ground frame = 10/gamma = 8.93028554974588 light-seconds

Time for tank to move exactly one full length in ground frame, so back wheel is at exactly the point the front wheel used to be: 8.93028554974588 ls/0.45c = 19.8450789994353 s

Position of front wheel after tank has moved one full length in ground frame, assuming back wheel was at x=0 at the start: x = 2*8.93028554974588 ls = 17.8605710994918 ls

So, if the marked point on the top track starts at the position of the back wheel, and by the time the tank has moved one full length it's at the position of the front wheel, then in the ground frame dx/dt for the marked point is (2*8.93028554974588)/(8.93028554974588/0.45) = 2*0.45 = 0.9 light-seconds/second.

If we know the coordinates where the top track marked point is at the front wheel are x=17.8605710994918, t=19.8450789994353 in the ground frame, then in the tank frame this translates to x'=10 and t'=1.11978502191171*(19.8450789994353 - 0.45*17.8605710994918)=13.2222222..., so the velocity of the top track marked point in the tank frame must be 10 ls/13.22222... s = (990/99)*c / (1309/99) = 990c/1309 = 90c/119 = 0.75630c, exactly equal to what you get below:

Yes I have a bad habit of rounding off. Pure mental inertia.

Since the top track marked point is moving at 0.9c in the ground frame, while in the tank frame the ground is moving at -0.45c, if you want to figure out the velocity of the marked point in the tank frame you have to plug in -0.45c in the velocity addition formula rather than +0.45c, which I assume is what you actually did since (0.9c - 0.45c)/(1 + (0.9c)*(-0.45c)/c^2) = 0.45c/0.595 = 90*0.005c/119*0.005 = 90c/119 = 0.75630c.

Yes I realized later I should not have posted the absolute value of -.45 which I did simply for simplicity and keeping all the velocities positive.

I think the confusion here may be that some people are thinking that if someone says a point on the top track is moving at 0.9c in the ground frame for a tank moving at 0.45c in that frame, they think this was obtained by assuming the point on the top track moved at 0.45c in the tank frame and then adding this to the velocity of the whole tank in the ground frame, which would be an incorrect addition of velocities in relativity. But in reality, when you understand that the point on the top track actually moves at 0.75630 in the tank frame, then you can see it makes sense that it'd move at 0.9c in the ground frame according to the relativistic velocity addition formula, since (0.45c + 0.75630c)/(1 + 0.45*0.75630) = 1.2063c/1.340335 = 0.9c.

Of course, all of these numbers are based on one key assumption made in your diagram: that the time for the marked point on the top track to go from the back wheel to the front wheel is the same as the time for the marked point on the bottom track to go from the front wheel to the back wheel, as seen in the ground frame! This doesn't necessarily have to be the case--you could equally well assume that in the tank frame the time for each marked point to go from one wheel to another is the same in both cases, since it can't be true in both frames (unlike in Newtonian physics where the times could be equal in all frames). So it really depends on your assumptions [/]about how this fantasy tank moving at relativistic speeds actually works,.

Total agreement on the crucial role of assumptions in this question. That has in fact been my position from the beginning.
That the OP has posed a question that may not be subject to resolution simply on the basis of applied principles of SR but finally might rest on the assumptions of physics you start with.
Both perspectives and solutions presented apparently disfunctional conditions for any possible actual mechanism.

2) Even if this assumption should be correct it still ignores the physics and measurement in the Earth frame.
If you apply the distance traveled according to the .74844 figure (Ich's) and then apply contraction on top of this you get a track point (segment) that has not traveled as far as the wheel base and gearing.
The contraction figure for the base is .8930 and for the track is .6632.
SO either something is amiss or the track should decompose. This of course may be the answer to the engineering side of the question; I.e. a .45c tank is just not a vialble physical possibility.
There are the additional questions; in the tank frame both the top and bottom are moving and so would be equally contracted.
In the Earth frame the top would be contracted but not the bottom .

Perhaps this all just "proves" tanks don't make good relativistic vehicles?

[

I did logical analysis working explicitly with Ich's firgure of .7844c
My point wasn't that either one was right or wrong but rather that both solutions had problems and created situations which seemed to negate the basis of both view's logical premises:i.e. " It must be this way or the tank won't work"

I maintained this open viewpoint up until I actually applied simultaneity. WHereupon I began to think that basic principles could in fact produce a resolution.

I think perhaps you missed a post.
This was when I had only applied simultaneity as a mental construct but the implications seemed to rule out the possibility of equal velocity measurement in the tank frame.

Hi calebholiday
You definitely provided a provocative ,even if not unsolvable scenarioo.

Some thoughts:

From the ground frame the clocks at the front wheelbase of the tank are running behind the clocks at the rear.
This would mean that measurement of track speed of the upper track would be faster than that measured for the bottom track.
As we know the bottom track velocity is 0.45c this would mean that the top track velocity must be greater than 0.45c
From the tank frame the reciprocal situation prevails.

The rear clocks are running behind so the measurement of the wheel base velocity must be lower. This is symmetrical with the clocks on the tank and both derive 0.45c as expected.

But in this case the top track is moving in the same direction as the wheel base so the desynchronization does not change the measurement as it is the exact same clocks measuring both.
So in this case the geometry and mechanics would seem to indicate twice the distance covered and hence twice the velocity i.e. 0.9c

So it would appear that in the light of simultaneity you may have been right all along.

There still remains the problem of reciprocal contraction:

It can be seen that in the tank frame the number of segments counted for the upper track would be increased due to simultaneity and therefore the conclusion would be they were contracted.
If there is a marked segment to start the velocity measurement and the rear observer starts counting segments from that point, he will count more segments passing in the time it takes the clock in the front to catch up as that first segment reaches his position.But of course the opposite would seem to pertain wrt the bottom track where they would count fewer segments.

Likewise in the ground frame I can see no way that the count starting in the rear, where the clock is running behind could not count fewer segments in the interval between time there and the same time at the front where the clock is running ahead.

So there is still seems to be good reason to think that your question has yet to be fully or satisfactorily resolved.
There remains the purely SR question of reciprocal contraction as well as the engineering/physics question of whether such a system is possible or would decompose before ever attaining such velocities.
The fundamental question of the meaning of contraction i.e. kinematic vs physical , itself appears to be unresolved and far from concensus.
Thanks for bringing forth interesting problem

whether in the tank frame the material is more bunched up on one top track and more stretched out on the other track (which would be true under your assumptions), or whether in the tank frame the material is equally stretched in both frames (which would be true if there were equal times in the tank frame for each spot to go from one wheel to another).

As you can see above, under my assumption the track would not be bunched up but would be counted as having more segments due to the desynchronization between front and back, as measured in the track frame.
My initial assumption after applying simultaneity was that due to this desynchronization it was not possible for the tank to measure equal velocities for top and bottom, even if the actual velocities were the same. At that time I placed no quantitative figure on the tank measurement, but only infered that it must be different. Otherwise it couldn't be consistent with the events of measurement of the tank velocity itself, which have to agree in both frames.
Based on your post I see I may have to do the inverse analysis from the tank frame that I , through inertia, avoided as superfluous.

In any case I still think this is a great scenario that has yet to be resolved or outlive its interest.

Thank you for your objective and insightful responce

 

[JesseM]

As you can see above, under my assumption the track would not be bunched up but would be counted as having more segments due to the desynchronization between front and back, as measured in the track frame.

What do you mean by "more segments" though? Suppose we paint two dots on the track, as in the example I posted in response to Ich--would you agree the number of segments between the two dots should stay constant as the pair of dots moves from the bottom to the top? If so, the segments would have to change length in the frame where both dots were at rest (the rest frame of that section of the material that makes up the tracks), depending on whether the dots were both on top or both on the bottom.

 

[Ich]

Not true

Oh no, JesseM, now we're 122 posts and a few lightyears from the original post.
We started with a tank, and a velocity addition problem. We had the assumption of vtop=0.9, and we actually had a paradox based on this assumption.
When you change the scenario now to the equivalent of two cannons shooting bullets back and forth at different speeds, there's not much left to discuss. This is trivially possible and therefore totally uninteresting, IMHO.

 

[JesseM]

Oh no, JesseM, now we're 122 posts and a few lightyears from the original post.
We started with a tank, and a velocity addition problem. We had the assumption of vtop=0.9, and we actually had a paradox based on this assumption.
When you change the scenario now to the equivalent of two cannons shooting bullets back and forth at different speeds, there's not much left to discuss. This is trivially possible and therefore totally uninteresting, IMHO.

OK, what was the original paradox if vtop was 0.9c? vtop is 0.9c in Austin0's example (in the ground frame), so if you say Austin0's example is "trivially possible and therefore totally uninteresting", what assumption is he making which is different from the original assumption? I've read the first few posts on this thread, it seems to me that calebhoilday was just mistaken in this paragraph:

The member of the design team states that if you treat the tank as the stationary observer, then what ever speed the top-side has the bottom-side needs to have, just in the opposite direction. If this is not the case then the tank tracks would rip apart, as either the top-side or bottom-side tracks would not feed enough track to the other.

As I showed in my example, as long as the material of the track is somewhat stretchable it's not actually necessary for the speed to be the same on top and bottom in the tank frame; if you have a series of dots drawn on the track which are 0.45 light-seconds apart when they're on the bottom, but 0.75630 light-seconds apart when they're on the top, then with the bottom side moving at 0.45c and the top side moving at 0.75630c, the top will feed the bottom a new dot once every second, and the bottom will feed the top a new dot once every second. So each side can feed the other the right amount of track and there's no need for the track to rip apart despite the difference in velocities in the tank frame.

In post #8 you responded to the part of calebhoilday's post above by saying:

From this (valid, btw) logic it is clear that the top side has v=0.45 and the bottom side has v=-.45.

But the logic isn't valid! Austin0's post, plus my addition of the dots on the track, shows that the amount of track on top and bottom will be perfectly stable even if the speed of the two sides is different in the tank rest frame.

 

[Austin0]

From the ground frame the clocks at the front wheelbase of the tank are running behind the clocks at the rear.
This would mean that measurement of track speed of the upper track would be faster than that measured for the bottom track.
As we know the bottom track velocity is 0.45c this would mean that the top track velocity must be greater than 0.45c
From the tank frame the reciprocal situation prevails.

The rear clocks are running behind so the measurement of the wheel base velocity must be lower. This is symmetrical with the clocks on the tank and both derive 0.45c as expected.

But in this case the top track is moving in the same direction as the wheel base so the desynchronization does not change the measurement as it is the exact same clocks measuring both.
So in this case the geometry and mechanics would seem to indicate twice the distance covered and hence twice the velocity i.e. 0.9c

It can be seen that in the tank frame the number of segments counted for the upper track would be increased due to simultaneity and therefore the conclusion would be they were contracted.
If there is a marked segment to start the velocity measurement and the rear observer starts counting segments from that point, he will count more segments passing in the time it takes the clock in the front to catch up as that first segment reaches his position.
But of course the opposite would seem to pertain wrt the bottom track where they would count fewer segments.

Likewise in the ground frame I can see no way that the count starting in the rear, where the clock is running behind could not count fewer segments in the interval between time there and the same time at the front where the clock is running ahead.

What do you mean by "more segments" though? Suppose we paint two dots on the track, as in the example I posted in response to Ich--would you agree the number of segments between the two dots should stay constant as the pair of dots moves from the bottom to the top? If so, the segments would have to change length in the frame where both dots were at rest (the rest frame of that section of the material that makes up the tracks), depending on whether the dots were both on top or both on the bottom.

No argument ; the number of segments between dots would be constant.
I think we may be taking two approaches to the same thing.
Having given more thought to my hasty "more segments" idea I have seen that I was simply wrong. In fact I got it reversed.
The count would be more on the bottom and less on the top.
Assume the rear tank observer on top ,starts counting segments from the marked segment at the beginning of the time trial. He just keeps a log of segment number and time.
When the marked segment reaches the midpoint of the front wheel the watch stops and from that elapsed time the rear observer can consult his log and see how many segtments had passed at that simultaneous time according to their clocks. This would mean that at the elapsed time at the front it would correlate to a past time at the rear i.e. less segments counted.
It seems that the reciprocal effect would pertain to the bottom , no??

How this would relate to contraction or stretching I am not yet sure but it seems like it should be a factor ?

Would you agree to my basic proposition that given the desynchronization between front and back , even if the actual velocities of the top and bottom were equal , the measured velocities could not be??

What conditions would have to exist for the two measured speeds to be the same??
It appears to me that it is clear; the top speed would have to be significantly lower than the bottom for the measurements to be the same. Yes?

This is pertinent to the tank frame where the two measurements are taken in different directions i.e. the top track is moving counter to the bottom so the desynchronization effect is in opposition.

Also counter to the ground frame velocity measurement.

In the ground frame the critical measurements are in the same direction;
the top track is moving in the same direction as the tank so the desynchronization effect is not in opposition but applies equivalently to both measurements.
But counter to the bottom track measurement so this is symmetrical with the tank frame
and both frames agree on the velocity of the bottom relative to the tank.

Does this all track??

[EDIT] scratch all the last part. I ran the numbers and the situation is completely symmetrical. Calculating simultaneity from the tank frame still leaves the problem intact. I.e. the ground frame calculates 0.74844074844074970834424639216174 for the top track. SO I am beginning to return to my original thought; that kinematics may not be able to resolve the problem and indicate a clear correct frame to apply the addition of v equation from.

But there is the clear preference for the ground frame on the basis of acceleration.
Not only has the tank undergone acceleration getting up to speed but it is under constant acceleration as it travels.
Normal force maintaining ground contact. Acceleration of the bottom track by the earth. Acceleration by the drive wheel that must propagate throughout the track smoothly, without slack or bunching, for the tank to move.
So to be consistent with the twins rationale the tank frame is not valid and the ground rules,,,maybe?

Additional thought; In the context of my workup above ,the velocity of the top track was not an argument. It was derived on the assumption of distance traveled . If you posit a velocity less than ..756430 like .45 this would mean that at the end point arrived at through the wheel base travel, the marked segment would be only approx .667 of the way there while the comparable bottom segment would have traversed the complete length. This is apparently unacceptable as far as viable mechanics. ANd throws out any ideas of equal distribution or equal transfer of segments between top and bottom. Or so it appears to me.
Of course the inverse is equally true. Given a lesser velocity of the top in the ground frame creates the same problem , no?

 

[Austin0]

Because it shows that the "2v-claim" - which seems so reasonable - would actually lead to breaking the tracks, while velocity addition preserves them. The proof is relatively simple, as neither the stretching of the tracks nor simultaneity are relevant.

That was not meant dismissively, it was meant to say that I posted all the formulas you need to follow the proof. You don't have to look elsewhere.

Then there's the issue of different track lengths (top vs bottom). Austin0 claimed this as evidence for undue stresses in the ground frame, without further thoughts or calculations. I dismissed that "evidence" claiming that he forgot the relativity of simultaneity.

Your example (which I understand now for the first time - if at all) is basically the same. Its resolution depends on physical stretching, lorentz contraction, and relativity of simultaneity, so it's necessarily complicated. I did not expect you to solve it.

First, the stretching of the track, in the tank frame:
I'm asking for the rest length of the track.
We have in the tank frame a length 2*l (top+bottom). But this is made up of Lorentz-contracted track.
If the contracted track has a length of 2*l, its rest length must be $2 l /0.893 = 2.24 l$.
So either the track has a length of 2.24l from the beginning (a very loose fit), or it gets stretched to this rest length during spin-up.

Now in the ground frame:
The top track is .893l long in that frame, and is made up of contracted track with a factor of 0.663. So the rest length of the upper track is $0.893 l/0.6632 = 1.347 l$
The bottom track is also .893l long in that frame, but it is not contracted at all. So its rest length is $0.893 l$.

Consistency check: the sum of both rest lengths is still 2.24l. Of course, there is no difference if we look at the same situation in different frames.

Now, does the result mean that the top track is severely stretched, while the bottom track is compressed?
No. Here's the appearance of Relativity of Simultaneity:
In the tank frame, at the rear wheel, there's track going from bottom to top at a constant rate. The rate in terms of contracted track is v, in terms of track rest length it is therefore $\gamma v = 1.12 v$.
The same amount goes down at the front wheel.
Everything is balanced.

In the ground frame, however, with its simultaneity convention, we see the rear wheel at a later time than the front wheel. It is, so to speak, $\Delta t =\gamma l_w v = l v =0.45 l$ older (tank time) than the front wheel.
In that tank time, a track rest length of $dl=1.12 v \Delta t = 1.12 v^2 = 0.227 l$ went up.
That means, instead of the equilibrium amount of 1.12l we see 1.12+.227=1.347 track rest length at the top, and 1.12-.227 = 0.893 at the bottom.
Not because there's additional stress, it's because we use a different simultaneity in the ground frame, where we measure the track at the rear wheel at a later (tank) time, where some of it already went up that did not come down at the front wheel.

I think it's fair to say that this is complicated stuff. And if I say that a newcomer has exactly zero chance of getting such things right, that's neither arrogance nor ad hominem, it's how it is.

Could you explain how that works; I.e. How the rear wheel could be at a later time than the front wheel in the ground frame?
If you mean from the ground frame the clock on the tank in the rear would be running ahead it would make sense, but what does that have to do with measurements in the ground frame?
How in the ground frame the front clock could be running behind the rear clock??

 

[JesseM]

No argument ; the number of segments between dots would be constant.
I think we may be taking two approaches to the same thing.
Having given more thought to my hasty "more segments" idea I have seen that I was simply wrong. In fact I got it reversed.
The count would be more on the bottom and less on the top.

Yes. If we want to have an integer number of segments, we might say there are 200 segments on the bottom at any given moment in the tank frame, and 119 segments on the top. So each segment on the bottom would have a length of 10/200=0.05 in the tank frame, which means that moving at 0.45c, a new segment would reach the back wheel every 0.05/0.45 = 1/9 of a second. And each segment on top would have a length of 10/119 in the tank frame, which means that moving at 90c/119 = 0.75630c, a new segment would reach the front wheel every (10/119)/(90/119) = 10/90 = 1/9 of a second too. So the rate at which the back wheel was feeding new segments to the top would equal the rate at which the front wheel was feeding new segments to the bottom, and the number of segments on each side would remain constant.

Assume the rear tank observer on top ,starts counting segments from the marked segment at the beginning of the time trial. He just keeps a log of segment number and time.

OK, in my example above he counts 9 segments per second.

When the marked segment reaches the midpoint of the front wheel the watch stops and from that elapsed time the rear observer can consult his log and see how many segtments had passed at that simultaneous time according to their clocks. This would mean that at the elapsed time at the front it would correlate to a past time at the rear i.e. less segments counted.

As long as we're talking about observers at rest in the tank frame, and they both start and stop counting segments that pass them simultaneously in the tank frame, then each will count 9 segments/second and thus they should count the same total number of segments having passed them.

Would you agree to my basic proposition that given the desynchronization between front and back , even if the actual velocities of the top and bottom were equal , the measured velocities could not be??

What do you mean by "desynchronization"? If we have clocks at the front and back wheel, then what frame are they synchronized in? And what do you mean by "actual velocities of the top and bottom"--"actual" in what frame? And in what frame are you taking the "measured velocities"?

What conditions would have to exist for the two measured speeds to be the same??
It appears to me that it is clear; the top speed would have to be significantly lower than the bottom for the measurements to be the same. Yes?

Again I'm not clear on what frames you're using to talk about speeds and measurements. It would be possible to alter your example so that in the tank frame both the top and bottom were moving at 0.45c in opposite directions, if that helps.

This is pertinent to the tank frame where the two measurements are taken in different directions i.e. the top track is moving counter to the bottom so the desynchronization effect is in opposition.

Also counter to the ground frame velocity measurement.

In the ground frame the critical measurements are in the same direction;
the top track is moving in the same direction as the tank so the desynchronization effect is not in opposition but applies equivalently to both measurements.
But counter to the bottom track measurement so this is symmetrical with the tank frame
and both frames agree on the velocity of the bottom relative to the tank.

Does this all track??

[EDIT] scratch all the last part. I ran the numbers and the situation is completely symmetrical. Calculating simultaneity from the tank frame still leaves the problem intact. I.e. the ground frame calculates 0.74844074844074970834424639216174 for the top track.

I don't understand what you're calculating there.

SO I am beginning to return to my original thought; that kinematics may not be able to resolve the problem and indicate a clear correct frame to apply the addition of v equation from.

...and I don't understand what "problem" you think kinematics can't resolve. Keep in mind I haven't read the whole thread--can you summarize what you're trying to work out here, and what the problem in your mind is?

Additional thought; In the context of my workup above ,the velocity of the top track was not an argument. It was derived on the assumption of distance traveled . If you posit a velocity less than ..756430 like .45 this would mean that at the end point arrived at through the wheel base travel, the marked segment would be only approx .667 of the way there while the comparable bottom segment would have traversed the complete length.

Don't get this either. If both the top and bottom are moving at 0.45c in the tank frame, then in the tank frame a segment on the bottom will take the same time to travel from one wheel to another as a segment on top, right? If you agree with that, what are you talking about when you say "the marked segment would be only approx .667 of the way there while the comparable bottom segment would have traversed the complete length"?

 

[Ich]

Keep in mind I haven't read the whole thread

Yes, that's an issue here. We've very early said that the tank should behave generally like a track vehicle, not an extrusion machine. For example, Ken Natton https://www.physicsforums.com/showpost.php?p=2808361&postcount=22" it as two wheels with a track around them. Such specifications set certain restrictions to the velocities, which make the problem interesting. So I don't want to get things muddled up after the end of the initial discussion.

Of course, it's ok if you like to discuss your very general notion of a track vehicle now. in that case, I don't disagree with you.

 

[Ken Natton]

Perhaps I don’t need particularly to defend myself here, I realize you don’t particularly intend any criticism of me, Ich. But just for the record, I always understood that real tanks have a complex arrangement of multiple wheels. I just conceived it as a single front and back wheel because it seemed to me to distil the problem, as I saw it at least, down to its essentials. The original problem was specified by Cabelholiday, but the YouTube clip he referred us to was of a model that had just three wheels. The extra central wheel was actually just the device that enabled it to ascend and descend staircases, which was actually what the clip was meaning to demonstrate.

If I might presume to summarise for you JesseM, as the thread’s title suggests Cabelholiday’s original poser was meant to challenge the velocity addition / subtraction formula. A significant part of the thread has been a non too constructive argument about whether the top track runs at 2v or at the value arrived at by employing the velocity addition formula first derived by Einstein in his famous special relativity paper of 1905. I don’t wish to reopen that dispute but I did try to suggest that a questioning of that formula is nothing specific to the tank track problem in the hope of keeping attention on what I saw as the real tricky problem offered by this poser. Ich showed admirable patience in guiding me to the answer I sought. Some of the thread’s most prominent posters believe the problem remains unresolved. Several others have expressed their opinion that it has long since been addressed.

 

[Ich]

Perhaps I don’t need particularly to defend myself here, I realize you don’t particularly intend any criticism of me, Ich.

Not at all, what you stated is exactly how I (and, I'm sure, the other contributors who gave up earlier) understood the OP. This is what we've been discussing, not machines that forcefully stretch and shrink the track every turn. Just the essentials, they are complicated enough.

 

[JesseM]

Yes, that's an issue here. We've very early said that the tank should behave generally like a track vehicle, not an extrusion machine.

What's an "extrusion machine"? Are you saying it should be impossible for the track to be the slightest bit flexible, so two dots painted on the track should always be precisely the same distance apart in the mutual rest frame of the two dots? Perfectly rigid objects are impossible in relativity, so this doesn't seem realistic... For example, Ken Natton

https://www.physicsforums.com/showpost.php?p=2808361&postcount=22" it as two wheels with a track around them.

Yes, and if the track is just a bit rubbery, it's not at all unrealistic that the section of the track between the tops of the wheels could be slightly more stretched than the section of the track between the bottom of the wheels. You could demonstrate something like this with two spools and a rubber band, for example.

Of course, it's ok if you like to discuss your very general notion of a track vehicle now.

It's rather absurd to suggest that a slight amount of stretching/compression of the track requires a very general notion of a track vehicle. And in any case calebhoilday's logic here in the opening post, which you called "valid", was:

The member of the design team states that if you treat the tank as the stationary observer, then what ever speed the top-side has the bottom-side needs to have, just in the opposite direction. If this is not the case then the tank tracks would rip apart, as either the top-side or bottom-side tracks would not feed enough track to the other.

calebhoilday wasn't just saying that the tracks would rip apart if the material was more stretched on one side than the other, he was saying they would rip because "the top-side or bottom-side tracks would not feed enough track to the other". Do you agree that this is incorrect, since my analysis shows that if we have a series of regularly-spaced dots on the track, the front wheel is feeding dots to the bottom track at exactly the same rate that the back wheel is feeding dots to the top track?

 

[Ich]

What's an "extrusion machine"? Are you saying it should be impossible for the track to be the slightest bit flexible, so two dots painted on the track should always be precisely the same distance apart in the mutual rest frame of the two dots?

Extrusion machines are not impossible, and the track has to be stretched (or lengthened) anyway. It's just that the tank we considered does not act like an extrusion machine, i.e. stretching and lengthening segments every cycle.

Yes, and if the track is just a bit rubbery, it's not at all unrealistic that the section of the track between the tops of the wheels could be slightly more stretched than the section of the track between the bottom of the wheels. You could demonstrate something like this with two spools and a rubber band, for example.

Yes, no problem. But that's not a tank. Remember, both spools/wheels have contact to the ground, they run at the same peripheral speed, the speed of the tank. And this constraint makes the problem well-defined and interesting for a discussion of relativistic velocity addition.
You rubber band is an engineering problem, nothing to do with SR.

Do you agree that this is incorrect, since my analysis shows that if we have a series of regularly-spaced dots on the track, the front wheel is feeding dots to the bottom track at exactly the same rate that the back wheel is feeding dots to the top track?

What you are proposing is something different. You can build such machines in principle, and you can of course discuss them, but they are not the tanks we discussed. For tanks run on the ground and have front and bottom wheel synchronized.

 

[Austin0]

The count would be more on the bottom and less on the top.

Yes. If we want to have an integer number of segments, we might say there are 200 segments on the bottom at any given moment in the tank frame, and 119 segments on the top. So each segment on the bottom would have a length of 10/200=0.05 in the tank frame, which means that moving at 0.45c, a new segment would reach the back wheel every 0.05/0.45 = 1/9 of a second. And each segment on top would have a length of 10/119 in the tank frame, which means that moving at 90c/119 = 0.75630c, a new segment would reach the front wheel every (10/119)/(90/119) = 10/90 = 1/9 of a second too. So the rate at which the back wheel was feeding new segments to the top would equal the rate at which the front wheel was feeding new segments to the bottom, and the number of segments on each side would remain constant.

Agreed the number would remain constant

Assume the rear tank observer on top ,starts counting segments from the marked segment at the beginning of the time trial. He just keeps a log of segment number and time.
When the marked segment reaches the midpoint of the front wheel the watch stops and from that elapsed time the rear observer can consult his log and see how many segtments had passed at that simultaneous time according to their clocks. This would mean that at the elapsed time at the front it would correlate to a past time at the rear i.e. less segments counted.

OK, in my example above he counts 9 segments per second.

As long as we're talking about observers at rest in the tank frame, and they both start and stop counting segments that pass them simultaneously in the tank frame, then each will count 9 segments/second and thus they should count the same total number of segments having passed them.

My proposal is that the observer at the top rear wheel in the tank frame would count 9/s for dt' -(4.4s) while the observer at the front bottom would count bottom segments for dt'+ (4.5s) and would therefore have a significantly different count. Just as the derived velocity of the bottom was different from the top.

Would you agree to my basic proposition that given the desynchronization between front and back , even if the actual velocities of the top and bottom were equal , the measured velocities could not be??

What do you mean by "desynchronization"? If we have clocks at the front and back wheel, then what frame are they synchronized in? And what do you mean by "actual velocities of the top and bottom"--"actual" in what frame? And in what frame are you taking the "measured velocities"?

In this context of the simultaneity workup I did , the desynchronization is between the front and back clocks of the tank as pbserved from the ground frame. Of course they are synchronized within the tank frame.
Sorry about the "actual velocities" ,,within the context of this thread I meant the velocities not as actual quantitative values but actual in the sense of the constraints enforced by physical principles and logic. I.e. I don't think anyone really disagrees with the evident logic that, independant of measurement ,the top and bottom must actually travel the same distance per time in the tank frame to be functional. I certainly never questioned this logic. The problem of course arises from the fact that the exact same logic and physical constraint applies equally in the ground frame.

What conditions would have to exist for the two measured speeds to be the same??
It appears to me that it is clear; the top speed would have to be significantly lower than the bottom for the measurements to be the same. Yes?

Again I'm not clear on what frames you're using to talk about speeds and measurements. It would be possible to alter your example so that in the tank frame both the top and bottom were moving at 0.45c in opposite directions, if that helps.

Yes I am aware of that, in fact that is exactly what the numbers referred to below are about. I did the same simultaneity analysis from the tank frame with the assumption of equal distance traveled by top and bottom in that frame and got the same figure as applying the addtion equation from that frame. I.e. Once again kinematics did not prefer or eliminate either solution.

I ran the numbers and the situation is completely symmetrical. Calculating simultaneity from the tank frame still leaves the problem intact. I.e. the ground frame calculates 0.74844074844074970834424639216174 for the top track.

I don't understand what you're calculating there.

SO I am beginning to return to my original thought; that kinematics may not be able to resolve the problem and indicate a clear correct frame to apply the addition of v equation from.

.

..and I don't understand what "problem" you think kinematics can't resolve. Keep in mind I haven't read the whole thread--can you summarize what you're trying to work out here, and what the problem in your mind is?

My position is that the OP has presented a unique and problematic question and scenario.
That has two mutually exclusive but equally valid logical bases for the application of the Addition o' V formula from different frames.
My analysis is one veiwpoint. You have provided a counter to Ich's objection to this view but no basis for eliminating the other solution or a clear preference for either one.
AS you pointed out and I confirmed my analysis is also reciprocal.
To this point it seems clear that that applies to all analyses so far.
Ich's showed how that viewpoint could be workable in the tank frame but the physical implications in the ground were not so obviously workable.
So ,to this point kinematics being the A of V formula and simultaneity have not determined a clear answer or viewpoint. Neither has physical logic and mechanics.
The only somewhat unexplored factor is length contraction.

My "problem" is that, early on , a reasonable solution was presented and was accepted as "proven" on the basis that the numbers were consistent within the system.
Well of course the numbers were consistent. Having chosen a preferred perspective to apply the A of V equation they must be consistent.
But beyond that all , other considerations were dismissed and the case was determined to be closed.
But in fact the opposing perspective can be applied and the numbers come out just as consistent as has just been shown. SImply demonstrating consistency does not prove a proposition if there are alternative propositions that are equally consistent , true??
DO you think there is a clear cut answer among the alternatives so far presented?
Think of this. This question presents a scenario involving 3 frames. Tank and ground being somewhat inertial but the track being attached to both frames. The bottom is actually partially at rest in the ground frame while attached to the tank frame by drive wheels and in motion in that frame. The track is being accelerated by both frames through direct physical connection.
Can you think of a similar problem off hand?

Additional thought; In the context of my workup above ,the velocity of the top track was not an argument. It was derived on the assumption of distance traveled . If you posit a velocity less than ..756430 like .45 this would mean that at the end point arrived at through the wheel base travel, the marked segment would be only approx .667 of the way there while the comparable bottom segment would have traversed the complete length.

Don't get this either. If both the top and bottom are moving at 0.45c in the tank frame, then in the tank frame a segment on the bottom will take the same time to travel from one wheel to another as a segment on top, right? If you agree with that, what are you talking about when you say "the marked segment would be only approx .667 of the way there while the comparable bottom segment would have traversed the complete length"?

This was in the context of my analysis , as observed from the ground. It derived a top v of .7564 and a bottom v of .45 with both marked segments completely traversing from wheel to wheel top and bottom. If you then assume the bottom v stays .45 and the top v is reduced to .45 this would mean that for the same distance traveled by the wheel base the bottom would span the base but the top would only span some portion of the distance between the wheels.
Does this track?

Or comparably in the ground frame: If the wheel base travels its own length at .45 so v = dx/dt =.45 and the distance of the top of the rear wheel to the end position of the top of the front wheel is 2*dx as measured in the ground frame.
If you then use the .74844 velocity for the marked segment then .74844*dt must be significantly less than 2*dx...i.e somewhere in between the tops of the wheels. WOuld you agree??

 

[Austin0]

Perhaps I don’t need particularly to defend myself here, I realize you don’t particularly intend any criticism of me, Ich. But just for the record, I always understood that real tanks have a complex arrangement of multiple wheels. I just conceived it as a single front and back wheel because it seemed to me to distil the problem, as I saw it at least, down to its essentials. The original problem was specified by Cabelholiday, but the YouTube clip he referred us to was of a model that had just three wheels. The extra central wheel was actually just the device that enabled it to ascend and descend staircases, which was actually what the clip was meaning to demonstrate.

If I might presume to summarise for you JesseM, as the thread’s title suggests Cabelholiday’s original poser was meant to challenge the velocity addition / subtraction formula. A significant part of the thread has been a non too constructive argument about whether the top track runs at 2v or at the value arrived at by employing the velocity addition formula first derived by Einstein in his famous special relativity paper of 1905. I don’t wish to reopen that dispute but I did try to suggest that a questioning of that formula is nothing specific to the tank track problem in the hope of keeping attention on what I saw as the real tricky problem offered by this poser. Ich showed admirable patience in guiding me to the answer I sought. Some of the thread’s most prominent posters believe the problem remains unresolved. Several others have expressed their opinion that it has long since been addressed.

WHo do you think is questioning the Addition of Velocities formula ? It is a question of from what frame and on what assumptions of measured velocity in that frame you apply it.
It has NEVER been a question of the validity of the equation itself. If you think so then I think you have misunderstood most of what has transpired IMHO I certainly can't speak for CalebHolidays original intent but that quickly became irrelevant.

 

[yossell]

Hi Austin0

I've read these last couple of pages a number of times, and with all the changes and revisions to the example, the numbers, the frame, the problem, I'm unable to easily follow the discussion between you and Jesse. This could be my fault. Is that nice picture of the tank you posted with the figures still valid? Or have we moved on?

Anyway, it may be helpful for some of us - and certainly for me - if you could give a quick, clear summary of, in the light of the recent posts, what you now think the problem is, what the figures are, what the issue is.

 

[Austin0]

Hi Austin0

I've read these last couple of pages a number of times, and with all the changes and revisions to the example, the numbers, the frame, the problem, I'm unable to easily follow the discussion between you and Jesse. This could be my fault. Is that nice picture of the tank you posted with the figures still valid? Or have we moved on?

Anyway, it may be helpful for some of us - and certainly for me - if you could give a quick, clear summary of, in the light of the recent posts, what you now think the problem is, what the figures are, what the issue is.

Hi yossell Yes the "nice " pic and figures are still valid but sadly inconclusive.

I am unsure if you read my last post to JesseM as he asked the same question and I tried to briefly answer.
In short it appears to me we have a plethora of valid logics and viewpoints with no clearcut unambiguous means of deciding which is more valid or really falsifying either one.
I could certainly be satisfied with either resolution if sufficiently justified.

We seem to be running shy of possible approaches to resolve this. Length contraction may be the only contender on its feet .
I just think this question is unique and interesting enough to be worth seeking a real answer. If we don't do it now I suspect it will return later at some point.

PS as I remember Fredrik first mentioned stretching wrt contraction and kev brought in springs between axles
and if you don't assume some counter to a physical conception of contraction then the tank don't go in any frame

 

[Austin0]

Attached drawing.

Tank:wheelbase length 10 ls in rest frame.

Starting the velocity test from the marked track points at the top point of the rear wheel (T₀)

and the bottom point of the front wheel (B₀).

Ground frame: x=o, t=0 , x'=0,t'=0 at rear wheel center

x= 8.930, t=0, x'=10, t'= (-4.5) at front wheel center.

At the point where the top track marked point is coincident with the top of the front wheel (T₁)and the bottom marked point is coincident with the rear wheel center (B₁) the coordinates are:

x=17.860 ,t=19.844 , x'=10 , t'=13.22 at the front wheel ...and

x= 8.930 , t=19.844 , x'=0 ,t'= 17.720 at the rear wheel.
_____________________________________________________________________________

TOP TRACK:

dx' = (T₁)- (T₀)=10

dt' =t'(T₁)-t'(T₀)= 13.22

v=dx'/dt' =10/13.22= .756429

BOTTOM TRACK:

dx'=(B₁) - (B₀) = abs(-10) =10

dt'= t'(B₁) - t' (B₀) = 22.22

dx'/dt'=10/22.22 =.450045

The final velocity for the top track as measured in the tank frame is .756429 c

The velocity returned by the Addition of velocities function for (.9 +.45) is .75630 c


2) If there is no error , in your qualified opinion is this sufficient reason to consider the correct solution to be .9 c for the top track in the ground frame??

3) Can you think of any conditions that would be consistent with these events and still justify a measurement of .45 for the top in the tank frame?

In any case there are still interesting, unresolved questions regarding contraction and physics in this scenario.

Hi Austin0

I've read these last couple of pages a number of times, and with all the changes and revisions to the example, the numbers, the frame, the problem, I'm unable to easily follow the discussion between you and Jesse. This could be my fault. Is that nice picture of the tank you posted with the figures still valid? Or have we moved on?

Anyway, it may be helpful for some of us - and certainly for me - if you could give a quick, clear summary of, in the light of the recent posts, what you now think the problem is, what the figures are, what the issue is.

Hi yossell
I think I may possibly be able to offer a kinematic resolution to the basic question.
The correct application of the Addition of Velocities equation and physical assumptions are consistent with the original perspective I.e. As applied from the ground frame on the assumption of 0.9 c measured velocity of the top track.

The basis for this is as follows:
Taking Ich's derived velocity from the assumption of equal but opposite velocities in the tank frame ---- 0.74844 c for the measured velocity of the top track in the ground frame
and applying it within the ground frame, results in the marked point of the top track not completing the traversal from the top of the rear wheel to the top of the front wheel in the time that the bottom marked segment makes the complete translation.
Refering to the original drawing where the tank wheelbase moves its own length at 0.45 in the ground frame and the distance between the initial position of the top of the rear wheel and the final postion of the top of the front wheel is dx=17.860 as measured in the ground frame.
If we apply the derived velocity of 0.74844 to the marked top track segment and determine it's final position we get;... (dt19.844)*0.74844 = dx = 14.85204336 which is short of the opposite wheel center at x=17.860 .

During the same time interval the bottom marked sgment has traveled dx=17.860 reaching the opposite wheel center.

Clearly this is an asymmetric , physically untenable situation on every level.

Likewise, in my original workup that derived a top track velocity of 0.756429 for the tank frame ;
If we instead insert the assumption of 0.45 velocity for the top marked segment in the tank frame , this results in (dt'=13.22)*0.45 =dx'= 5.94999 which is also only part of the way to the opposite wheel center while the bottom segment traverses the complete distance.

Additionally it appears that the percentage of the total distance traveled in each frame is significantly different suggesting a problem wrt frame agreement on local events although I haven't pursued this yet.

On the other hand , operating on the assumption of 0.9 for the top in the ground frame
results in equal distance traveled between the top and bottom in both frames, but with the measured velocity in the tank frame being greater than 0.45 as a purely kinematic consequence of the relativity of simultaneity.
Physical symmetry rather than measured symmetry in the tank frame.

Certainly I may be overly optimistic so I invite participation and critical analysis because I , for one ,would really like to get on to the questions still remaining regarding length contraction and how a workable tank might possibly arise from that conundrum.

 

[Ken Natton]

WHo do you think is questioning the Addition of Velocities formula ?

Austin0, I have had something of a debate with myself about whether there is any value in replying to you. I do not, for one moment suppose that I will persuade you of anything, and I don’t believe that there is any value in returning to the tenor of exchange that did occur at one point on this thread. The best I can hope for is a clarification of the difference between us that we can agree on.

Your contention is that it is consistent to argue that, in our example of v = 0.45c, the top track runs at 0.9c, and also to assert acceptance of the velocity addition formula. My contention is that contending that the top track runs at 0.9c is inherently a questioning of the velocity addition formula. Thus my answer to your question about who I believe is questioning it is anyone who contends that the top track runs at 0.9c. There are multiple contributors to this thread who have so contended.

 

[yuiop]

, results in the marked point of the top track not completing the traversal from the top of the rear wheel to the top of the front wheel in the time that the bottom marked segment makes the complete translation.

As soon as you say "in the time" for events that do not happen at the same place, it immediately suggests that you have a simultaneity problem and you do not seem to have taken account of this.

, Certainly I may be overly optimistic so I invite participation and critical analysis because I , for one ,would really like to get on to the questions still remaining regarding length contraction and how a workable tank might possibly arise from that conundrum.

Designs for a workable tank have already been given. Either make the tracks elastic or mount one the axles on horizontal springs. Something has to give. A rigid tank with rigid track segments that cannot stretch can not operate at relativistic speeds. Relativity forbids the existence of rigid materials. The discovery of a material that can not compress or stretch would invalidate SR and GR.

 

[Austin0]

As soon as you say "in the time" for events that do not happen at the same place, it immediately suggests that you have a simultaneity problem and you do not seem to have taken account of this.

Designs for a workable tank have already been given. Either make the tracks elastic or mount one the axles on horizontal springs. Something has to give. A rigid tank with rigid track segments that cannot stretch can not operate at relativistic speeds. Relativity forbids the existence of rigid materials. The discovery of a material that can not compress or stretch would invalidate SR and GR.

You say "suggests" I do not seem to have taken account of simultaneity.

Have you actually read the foregoing posts where I presented a specific simultaneity workup from the ground frame and referenced a similar workup I did from the tank frame?

DO you have any specific objection or correction to the simultaneity analysis that I have totally taken account of?
Or is this just an a priori assumption based on taking a few words out of context and running with them??
I welcome actual participation and critical analysis and if you find actual flaws in my analysis I will move onward
but amorphous assertions based on your assumptions are not helpful.

Did you actually read enough to have any understanding of the basis of the conclusion?

As for the last part of your responce if you will look at the previous post to yossell you will find that I stated what you have said here and even mentioned you.
If you think that simply the assumption of some stretch or a couple of springs negates any questions wrt relative contraction you are entitled to your opinion.

 

[Austin0]

Austin0, I have had something of a debate with myself about whether there is any value in replying to you. I do not, for one moment suppose that I will persuade you of anything, and I don’t believe that there is any value in returning to the tenor of exchange that did occur at one point on this thread. The best I can hope for is a clarification of the difference between us that we can agree on.

Your contention is that it is consistent to argue that, in our example of v = 0.45c, the top track runs at 0.9c, and also to assert acceptance of the velocity addition formula. My contention is that contending that the top track runs at 0.9c is inherently a questioning of the velocity addition formula. Thus my answer to your question about who I believe is questioning it is anyone who contends that the top track runs at 0.9c. There are multiple contributors to this thread who have so contended.

Ken Natton
DO you understand that I am applying the velocity addition formula?

That absolutely everything that I have done is consistent with that formula?

That up until the last few posts I never argued that the top velocity must be 0.9 ??

Could you perhaps clarify the logic that the proposition that the top v is 0.9 , is inherently questioning the addition of velocities equation??
I would sincerely like to know.