Slimy0233
- 167
- 48
- Homework Statement
- A ball is thrown up at a speed of 4.0 m/s. Find the
maximum height reached by the ball. Take ##g = 10 m/s^2##
- Relevant Equations
- ##v = u +at##
##S = ut +0.5(at^2)##
I realize I can solve the other way too. But I want to solve using the equations
##v = u +at##
##S = ut +0.5(at^2)##
and I don't know why I didn't get the right answer. Thank you for your help!

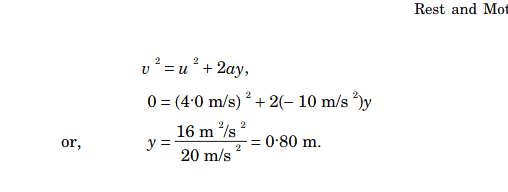
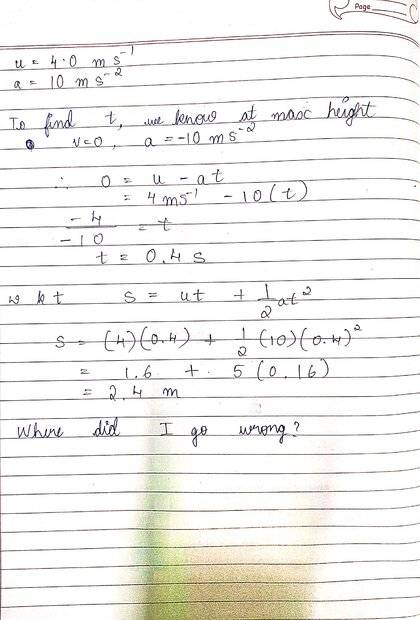
##v = u +at##
##S = ut +0.5(at^2)##
and I don't know why I didn't get the right answer. Thank you for your help!