"Max Power" Calculations in Electrical Engineering

[Femme_physics]

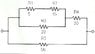
So in a question I have to find out what's the "max power" that can be spread around a circuit without causing any damage to the resistor. So, unsure what "max power" means, I googled "max power" and ended up with many images and resources of Homer Simpson, half naked girls and cars, with no referrence to the electrical engineering term. Where do I find some educational referrences to calculating the max power in the sense I need? I'm not looking for a full electronics guide, just an article with a specific referrence to that.

 

[Xarren]

To "the" resistor? Where is the resistor? What is the circuit?

Power is current x voltage. Max power usually the amount of power the component can dissipate as heat. If more power is applied, the component will melt/break.

Resistors have "power ratings" which tell you how much power can be allowed through it. Let's say you have a 10ohm resistor, with a power rating of 10w (watts, unit of power).

Let V = 5

V=IR

I=V/R

P=IV

P=(V/R)V

P=V^2/R

PR^1/2 = Vmax

This way you can find the maximum Voltage that can be applied to the resistor without damaging it.

 

[Femme_physics]

Well, this is the circuit (attached). There are 5 resistors. So if say each resistor has a 1W power, a total power of more than 5 will definitely cause damage?

 

[Studiot]

a total power of more than 5 will definitely cause damage?

Not necessarily.

Start by labelling the outer two terminals A and B.
Then ask yourself, "How could the power be applied?"

 

[MATLABdude]

Courtesy of IMDB:
Homer Simpson: Kids: there's three ways to do things; the right way, the wrong way and the Max Power way!
Bart: Isn't that the wrong way?
Homer Simpson: Yeah, but faster!
http://www.imdb.com/title/tt0701118/quotes?qt0229108

For junior electrical engineering students, max power refers to the optimal source impedance that leads to maximum power transfer to a load resistor:
http://en.wikipedia.org/wiki/Maximum_power_transfer_theorem

However in your case, this is probably referring to the maximum power (P = I * V) that can be dissipated in a resistor before it burns up / explodes / vapourizes. All resistors are rated for a maximum power dissipation (the most commonly encountered are 0.25 W, and they're usually darn toasty when you put this much power through them). Note also that this makes certain assumptions about the ability for heat to be carried away to keep the casing under 60 C (if I recall correctly).

Usually, the higher the power dissipation, the bigger the casing (for some reason, my Google-fu fails to find an image of various power-rating resistors lined up in a row):
http://www.curtpalme.com/forum/viewtopic.php?p=256721

Make sure your resistors dissipate under the specified maximum, and you should be good. Note that if a 100 ohm resistor has 250 mA going through it, you have 250 mW. However, if you have two 50 ohm resistors in series with 250 mA going through them, they each dissipate only 125 mW.

EDIT: Beaten to the chase! Exceeding 5W total is only a problem if you exceed 1W in any of the component resistors.

 

[Femme_physics]

Let V = 5

But if you don't know V?

Not necessarily.

Start by labelling the outer two terminals A and B.
Then ask yourself, "How could the power be applied?"

Hmm...I guess it could be applied in 3 ways Horizontally. In an arch over R1 and R2, or in an arch below R5. Does this affect the result? Because as far as I understand, there's only 1 answer.

 

[Femme_physics]

But if you don't know V?

I just realized I can extract V from the formulas for each of the R's.

Courtesy of IMDB:
Homer Simpson: Kids: there's three ways to do things; the right way, the wrong way and the Max Power way!
Bart: Isn't that the wrong way?
Homer Simpson: Yeah, but faster!
http://www.imdb.com/title/tt0701118/quotes?qt0229108

I'll have to watch this episode hehe

 

[Studiot]

In order to supply power to the circuit I presume they meant you to apply a voltage between terminals A & B. Call this voltage V. The power drawn will increase as V increases.

This allows you to calculate the currents in each resistor in terms of V
The total power is the sum of all the individual resistor powers.
Each individual resistor power is given by the square of the current (a function of V) and the individual resistance.
So you then need to let V increase until one of the individual resistor powers reaches 5 watts.

You can then use this value to calculate the total power.

 

[Xarren]

Well the battery voltage is the V in case of one resistor. If you have more than one resistor, Vs are distributed in ratios according to their resistances. Eg two 1ohm resistors and 5V supply = 2.5V across each resistor.

 

[Femme_physics]

I've been staring at this problem for a while now and I keep running into the same loop of confusion. I don't have V. The only thing I can do is define P = 1 at each at the resistor, and since I need Pmax I figured I can just add them up together. Apparently I can't.

This way you can find the maximum voltage that can be applied to the resistor without damaging it.

Yes, but I don't need maximum voltage, I need maximum power.

In order to supply power to the circuit I presume they meant you to apply a voltage between terminals A & B. Call this voltage V. The power drawn will increase as V increases.

Makes sense.

This allows you to calculate the currents in each resistor in terms of V

Right, but each resistor has its own V. I don't know what it is unless V is defined to me.

The total power is the sum of all the individual resistor powers.

Yes, that I do know, which is why I thought to just add 1+1+1+1+1 = 5 [W], and bang, problem solved, but it seemed too easy.

So you then need to let V increase until one of the individual resistor powers reaches 5 watts.

You can then use this value to calculate the total power.

But you've just defined Watt to be 5, why do I need to calculate it?

If you think I'm currently too low a level of an electronic student to understand this, I'll say fair enough. Sorry if I'm showing some n00bish elements. Pretty new to electronics. Thanks for all your help.

 

[I like Serena]

It seems to me your problem statement is incomplete.
Does it say for instance, how much power a resistor can take before blowing up?

 

[Femme_physics]

Yes, 1 [W]

 

[I like Serena]

All right!

Now let's say we put a voltage V on the left side (call it A), and set the right side (call it B) to Earth (that is a voltage of 0 V).

A current will start flowing that we will call Ia.

Let's take a look at resistor R₅ which is 50 ohm.
Since there is a voltage V, there will be a current I₅ = V / R₅ = V / 50.
The dissipated power in R₅ will be P₅ = V² / R₅ = V² / 50.

So we can say that if V is such that P₅ = 1 W, then R₅ will blow.
This would happen if V² / 50 = 1 W, which means V = √50 = 7.07 V

Now if we would calculate the Req of the circuit, we know that the total power dissipated in the circuit would be Pmax = V² / Req which you could already calculate.

Note that you would have to check the dissipated power in the other resistors as well, to see if they would already blow with a lower V.

 

[Studiot]

But you've just defined Watt to be 5, why do I need to calculate it?

Sorry I din't look properly, I thought the max was 5 watts for any resistor. Now I realize it is 1 watt.

Right, but each resistor has its own V. I don't know what it is unless V is defined to me.

V is applied between A and B

So the current in R5 is V/50

Now R1+R2 is 20,
put this in parallel with R3 the effective resistance is 10
add this to R4 to get 40

So the current in R3 is V/40

I will leave you to split this to calculate the currents in R1 and R2.

 

[Femme_physics]

I like Serena, I followed your lead verbatim. Attached. Do I get your seal? (btw come to think about it, this should've been posted in the HW section. I just didn't expect you all to be so nice and lead up to my question)

Note that you would have to check the dissipated power in the other resistors as well, to see if they would already blow with a lower V.

I will leave you to split this to calculate the currents in R1 and R2.

But I can just do Rtotal without having to calculate each separately, right?

 

[Studiot]

The voltage across R5 is V
The voltage across R4 is V times 30/40
The voltage across R3 is V times 10/40
The voltage across R2 is V times 10/40 times 15/20
The voltage across R1 is V times 10/40 times 5/20

Edit

I think it more important that you can follow the above, rather than that you can find a short cut, because this is really a test of your understanding of combined series and parallel circuits.

 

[Femme_physics]

The voltage across R5 is V
The voltage across R4 is V times 30/40
The voltage across R3 is V times 10/40
The voltage across R2 is V times 10/40 times 15/20
The voltage across R1 is V times 10/40 times 5/20

Edit

I think it more important that you can follow the above, rather than that you can find a short cut, because this is really a test of your understanding of combined series and parallel circuits.

Fair enough, but if they're asking me for Pmax why do I need to provide them results in terms of voltage across each R?

 

[I like Serena]

I like Serena, I followed your lead verbatim. Attached. Do I get your seal? (btw come to think about it, this should've been posted in the HW section. I just didn't expect you all to be so nice and lead up to my question)

But I can just do Rtotal without having to calculate each separately, right?

Sorry, no seal yet ;)

In your total resistance you were right in your calculation of R_1,2,3. But then you added the other resistors. This would only be correct if they were all in series, which they are not.

And in your second sheet you write that if Pmax=1, that R_T will blow.
But that's not correct either.
What you would have, is that with Pmax=V²/R_T=(√50)²/22.22=2.25 W, that R₅ will blow.

The resistor R_T as such does not exist - it is only an "equivalent" resistance.
If anything blows, it will be an individual resistor.
I have (randomly) picked the resistor R₅ to see when it would blow.
But any of the others may blow as well.

That's where Studiot's list might come in handy, because he's given you the voltages across each resistor. With each voltage and the corresponding resistance, you can calculate the power dissipated in each resistor with the formula P=V²/R

 

[Femme_physics]

I think this is too much for me. Thanks for trying. I've been trying to figure it out for a while but I'm only getting more confused. I don't understand how Studiot's list make sense, he just decided out of thin air that R5 equals = V? Maybe I have some gaps in my knowledge?...

In your total resistance you were right in your calculation of R1,2,3. But then you added the other resistors. This would only be correct if they were all in series, which they are not.

I added them in parallel where they're in parallel , then they became in series. That's how I've been doing it in class to get the right figures. Now I'm wrong with that, too? Great, I'm back to just knowing ohm's law, and even there my confidence is shaken :P

 

[I like Serena]

I added them in parallel where they're in parallel , then they became in series. That's how I've been doing it in class to get the right figures. Now I'm wrong with that, too? Great, I'm back to just knowing ohm's law, and even there my confidence is shaken :P

You can firm up your own beliefs again, because between your 2nd and 3rd drawing you did apply the law correct for parallel resistors!

In your third drawing you have R_1,2,3 in series with R₄, so those add up.
Then I guess you should have made a 4th drawing with R_1,2,3,4 which is in parallel with R₅...

I think this is too much for me. Thanks for trying. I've been trying to figure it out for a while but I'm only getting more confused. I don't understand how Studiot's list make sense, he just decided out of thin air that R5 equals = V? Maybe I have some gaps in my knowledge?...

You appear to be missing some knowledge about how voltages vary in a circuit, and how currents add up in a circuit.
This will come back when you get more knowledge about for instance Kirchhoff's circuit laws.
I had the impression you already knew about those.
My bad!

As to Studiot's list, he did not say that R5 equals V, but he wrote that the voltage "across" R5 is V.
This means that ohm's law is applicable, and you can find for instance the current "through" R5 with the formula I5=V/R5 (Ohm's law ).

 

[Femme_physics]

In your third drawing you have R1,2,3 in series with R4, so those add up.
Then I guess you should have made a 4th drawing with R1,2,3,4 which is in parallel with R5...

I went with the conclusion that the power source is wherever I want it to be. If the power sources are between the two points then yes, I'm aware that my drawings would be wrong. Shouldn't the power source be defined a location?

You appear to be missing some knowledge about how voltages vary in a circuit

I do know that each R has its own V. Based on the formula V = IxR

and how currents add up in a circuit.

I do know that in a series circuit I is constant, in a parallel circuit it splits, but only if we know V can we know I everywhere. In this problem we have neither I or V!

Kirchhoff's circuit laws

We went through
Sum of all I going in equals to sum of all I going out
Sum of all series V equals to Vtotal.

And I think that's it.

As to Studiot's list, he did not say that R5 equals V, but he wrote that the voltage "across" R5 is V.

The voltage across R5 is R5 x I, as far as I know.

 

[I like Serena]

I do know that each R has its own V. Based on the formula V = IxR

I think we're onto something here.
It's not that each R has its own voltage V, but each R has its own "voltage difference", usually denoted ΔV.

Imho it's usually easiest to assign each point "between" resistors a "voltage amount".
The "voltage difference" of a resistor is then the difference between the "voltage amounts" on either side of the resistor.

A more precise version of the formula is ΔV=IxR.

I do know that in a series circuit I is constant, in a parallel circuit it splits, but only if we know V can we know I everywhere. In this problem we have neither I or V!

Yes, that is correct. That is Kirchhoff's current law.

We went through
Sum of all I going in equals to sum of all I going out
Sum of all series V equals to Vtotal.

And I think that's it.

Yes, you seem to understand Kirchhoff's current law perfectly. :)

Kirchhoff's voltage law is a little more nuanced.
What is more precisely says, is that the sum of all "voltage differences" in a closed loop is zero.
This works out to what you say, if we're just talking about resistors in series.

The key however, is that we're not talking about a "voltage amount" but about a "voltage difference".
So we talk about a current "through" a resistor, which is the current in the resistor.
And we talk about the voltage "across" a resistor, which is the "voltage difference" over the resistor.

The voltage across R5 is R5 x I, as far as I know.

That's entirely right! :)

I went with the conclusion that the power source is wherever I want it to be. If the power sources are between the two points then yes, I'm aware that my drawings would be wrong. Shouldn't the power source be defined a location?

Confused

The power source would be for instance a battery with the positive pole on the left side of the circuit and the negative pole on the right side of the circuit. It is not part of the circuit.

This would cause a "voltage difference" across the entire circuit. And because it is a battery, this voltage would be constant, regardless of the current flowing.

Typically we would assign the left side of the circuit a "voltage amount" V, and the right side of the circuit a "voltage amount" 0.

 

[Femme_physics]

The power source would be for instance a battery with the positive pole on the left side of the circuit and the negative pole on the right side of the circuit. It is not part of the circuit.

Yes, I know, this was the circuit in my mind (attached). But I guess I'm not allowed to define the source wherever I want. It's just that it wasn't defined on the question or in the drawing, so I've taken the liberty, heh.

Thank you so much for the detailed reply and the encouragement Serena, and everyone. I'll try reading on some guides and going over my notes again to see how to solve this question. If I ever do solve it I'll post back here. Will definitely use all the replies here as referrence when I try. It might take time. But, anyway, even while having failures after failures, it's always good to try :) What doesn't kill you makes you stronger...even though in electricity it often just kills you. heh.

 

[Studiot]

I'm glad you know Kirchoff's laws.
However what I did is much more fundamental and can be done by inspection.
Since it seems like magic I will walk you through it (It is actually called a walking through analysis in electronics)

Firstly label the terminals A & B as I said. These are the small circles to the left and right of your diagram.
Apply any voltage V across these terminals. So V volts appears across AB.

Now R5 is connected directly across AB so the voltage across R5 is V.

In the other leg of the circuit you have a complicated arrangement containing R1 through R4.
However can you see that this leg is also connected directly across AB?
So the voltage across the whole leg is V.

R1 & R2 are in series and add up to 5+15 = 20
This series pair in in parallel with R3 and so is 20 in parallel with 20 = 10

So the second leg has 10 in series with R4 ie 10 in series with 30 a total of 10 + 30 = 40
As already noted the voltage across this is V
In a series circuit the total voltage (V in this case) is distributed in proportion to the resistances in series to the total.

So the voltage across R4 is 30/40 times V

And the voltage across the combination of R1, R2 & R3 is 10/40 times V.

This voltage (10V/40) is directly across R3 so is the voltage across R3.

It is also the voltage across the series combination of R1 and R2, again distributed in proportion

So voltage across R2 is 10V/40 times 15/20
and voltage across R1 is 10V/40 times 5/20

Now that we have all the voltages and resistances we can assemble an equation for the total power

$$Powe{r_{total}} = \frac{{V_{R1}^2}}{{R1}} + \frac{{V_{R2}^2}}{{R2}} + \frac{{V_{R3}^2}}{{R3}} + \frac{{V_{R4}^2}}{{R4}} + \frac{{V_{R5}^2}}{{R5}}$$

Substituting

$$= \frac{{{V^2}}}{{50}} + \frac{{{{\left( {\frac{{30V}}{{40}}} \right)}^2}}}{{30}} + \frac{{{{\left( {\frac{{10V}}{{40}}} \right)}^2}}}{{20}} + \frac{{{{\left( {\frac{{10V}}{{40}}*\frac{{15}}{{20}}} \right)}^2}}}{{15}} + \frac{{{{\left( {\frac{{10V}}{{40}}*\frac{5}{{20}}} \right)}^2}}}{5}$$

Now if we examine each of the 5 terms in this expression the one with the largest numerical coefficient of V² will be the one to reach the 1 watt limit first.

Do you follow this reasoning here?

If we set this equal to 1 watt we can solve for V

Then we can back substitute and determine the total power.

The arithmetic is not really so fearsome as it looks - really.

 

[Studiot]

Since I have done all the work for you in the votlage analysis, you could also perform a similar analysis with current instead of voltage.

Allow a current I to flow from A to B through your network and calculate the currents in each resistor in terms of I. (no voltage assumptions are required in this case)

Assemble a total power equation as before using power = (curent in each resistor)² time the resistance.
Solve for I using the term with the largest coefficient.
Back substitute I to get the total power.

go well

 

[Femme_physics]

You're incredible, Studiot. Absolutely incredible. I will definitely print this post and add to my notebook. I WAS able to follow you, actually, and fathom the concept thoroughly with this analysis and see exactly what you did. This is perfect. Exactly what I needed.

I'm not sure if I got my arithmatic right in the calculation I attached now but I understand how you got there. I'm not actually used to seeing a voltage source where the + is on one end and the - at the other-- it threw me off. Thank you for caring enough to post it, Studiot.


(The amount of care and help in this forum amazes me every time anew. It works because there are people like you around! What an educational treasure on the net. I never expected that.)

 

[Femme_physics]

Since I have done all the work for you in the votlage analysis, you could also perform a similar analysis with current instead of voltage.

Allow a current I to flow from A to B through your network and calculate the currents in each resistor in terms of I. (no voltage assumptions are required in this case)

Assemble a total power equation as before using power = (curent in each resistor)² time the resistance.
Solve for I using the term with the largest coefficient.
Back substitute I to get the total power.

go well

I will definitely do that as well.

 

[Studiot]

Whilst I agree with multiplying the equation through by 300, I don't make the second and later terms the same.

your 10 etc should appear ouside the brackets, not inside where you have them.

that is

$$\frac{{{{\left( {\frac{{30V}}{{40}}} \right)}^2}}}{{30}}*300 = 10*{\left( {\frac{{30V}}{{40}}} \right)^2}not{\left( {\frac{{300V}}{{40}}} \right)^2}$$

etc

Looking again at my 2 equations I see I have reversed the order of terms between the first and second, although both are correct. Sorry if that caused confusion.

 

[Femme_physics]

Right, algebra kinks. I will work it out better, thanks.

 

[Femme_physics]

$$= \frac{{{V^2}}}{{50}} + \frac{{{{\left( {\frac{{30V}}{{40}}} \right)}^2}}}{{30}} + \frac{{{{\left( {\frac{{10V}}{{40}}} \right)}^2}}}{{20}} + \frac{{{{\left( {\frac{{10V}}{{40}}*\frac{{15}}{{20}}} \right)}^2}}}{{15}} + \frac{{{{\left( {\frac{{10V}}{{40}}*\frac{5}{{20}}} \right)}^2}}}{5}$$
.

Shouldn't the first term -> V^2/50 have brackets separating the ^2 from the V/50?

 

[Studiot]

This is where I inadvertanly reversed the term order, relative to the first equation.

R5 = 50 so power in R5 is

V²/50

R5 is the only resistor that experiences the full voltage, V.
All the others see V reduced by some factor.
However you still need to check that R5 reaches 1 watt first, since we also divide by the resistor value to get the power.

I am off now for some parvus et circum in the shape of dinner and Alien v Predator 2.

go well

 

[Femme_physics]

I see. It's also a bit late here. I'll post tomorrow the numbers hopefully I'd get someone's seal of approval. Thank you Studiot, Serena.

 

[Femme_physics]

1) I've scanned my second attempt of the solution

2) I've also tried to calculate for I, is my equation correct?

Also, as far as how you've gotten the the formula for each of the resistor, it's basically:

"the potential difference of the resistor (or the entire parallel region), divided by the potential difference across the entire closed loop, divided by the potential difference of the resistor."

I've tried to derive that from your formula. I don't recall it being explained to me that way.

 

[Studiot]

Oh dear, you really are better at mechanics.

I will post some more after lunch. Meanwhile perhaps you would like to think about this.

Why does your 'solution' equate the total power to 1 and then 300?

The current method is not really derivable from the voltage method - V does not actually appear anywhere.

Kirchoffs laws, loops and such won't help here. I'm just using the basic definition of series and parallel connections, ohm's law and the equation for power.

 

[Femme_physics]

Oh dear, you really are better at mechanics.

LOL. Appreciate the recognition though.

I do know how to find Rt and easily break down a parallel+series circuit to an only series circuit, which I initially thought was challenging but I understand the simple principles of it.

Why does your 'solution' equate the total power to 1 and then 300?

Well, I solved for V, so since I had a fraction and 300 was my common denominator, I multiplied both sides...

So quote is not true? ->

"the potential difference of the resistor (or the entire parallel region), divided by the potential difference across the entire closed loop, divided by the potential difference of the resistor."

It seems to be true to how you've decided the formula for each R in your P equation.