zenterix
- 774
- 84
- Homework Statement
- The following problem is from MIT OCW's online 8.02, Electromagnetism. It has items (a)-(d), and my question is about (d). I will show calculations from all items before I get to item d) at the end.
Consider two oppositely charged objects located along the y-axis. The positively charged object has charge ##+q## and is located at ##y=+a##, and the negatively charged object has charge ##-q## and is located at ##y=-a##, forming an electric dipole along the ##y##-axis.
(a) Find an expression for the electric potential ##V(r,\theta)## at point ##P## assuming ##V(\infty)=0##.
(b) When ##r>>a##, use a Taylor series expansion to show that the electric potential can be approximated by the expression ##V(r,\theta)=k\vec{p}\cdot\hat{r}/r^2## where ##\vec{p}## is the electric dipole moment and ##\hat{r}## is the radial unit vector in polar coordinates.
(c) The component of the electric field in polar coordinates is given by the expressions
$$E_{\theta}(r,\theta)=-\frac{1}{r}\frac{\partial}{\partial\theta}V(r,\theta)$$
$$E_{r}(r,\theta)=-\frac{\partial}{\partial r}V(r,\theta)$$
Calculate the components of the electric field in polar coordinates at point ##P## associated with your "dipole approximation" in part (b).
(d) A positively charged dust particle with mass ##m## and charge ##+q## is released from rest at point B (not shown on the drawing) located on the y-axis at the point given by coordinates ##(d,0)##, ##d>a##. In what direction will it accelerate? What is the speed of the particle when it has traveled a distance ##s## from its original position at point B? Answer this question using the exact formulas, not the approximation in part b.
- Relevant Equations
- My doubt is specifically about item d. I will quickly show the calculations for a, b, and c before showing my thoughts on d.
Here is a depiction of the problem
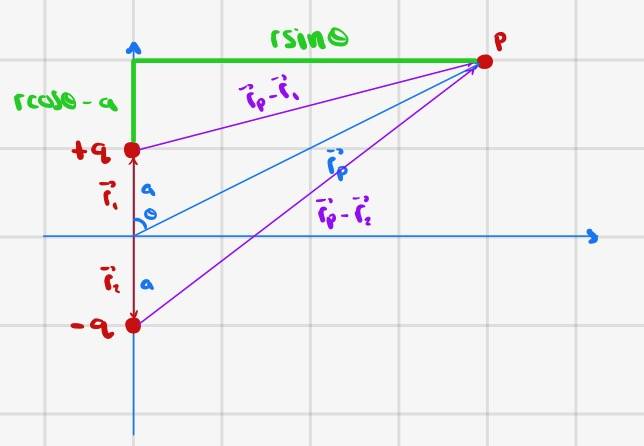
a) The potential at any point P due to a charge q is given by ##\frac{kq}{r}=\frac{kq}{\lvert \vec{r}_s-\vec{r}_P \rvert}##, where ##r## is the distance from the charge to point P, which is the length of the vector difference between ##\vec{r}_s##, the position of the source charge, and ##\vec{r}_{P}##, the position vector of point P.
Since we have two charges, we compute the potential at a point P using superposition.
Let point P have coordinates ##(x,y)##. Then
$$\vec{r}_1=a\hat{j}$$
$$\vec{r}_2=-a\hat{j}$$
$$\vec{r}_P=x\hat{i}+y\hat{j}$$
$$\lvert \vec{r}_P-\vec{r}_1\rvert = \lvert\langle x,y-a\rangle\rvert=\sqrt{x^2+(y-a)^2}$$
$$\lvert \vec{r}_P-\vec{r}_2\rvert = \lvert\langle x,y+a\rangle\rvert=\sqrt{x^2+(y+a)^2}$$
Thus, by superposition we have
$$V_P(x,y)=\frac{kq}{\sqrt{x^2+(y-a)^2}}+\frac{k(-q)}{\sqrt{x^2+(y+a)^2}}$$
Using
$$x=r\sin{\theta}$$
$$y=r\cos{\theta}$$
we can write ##V_P## in polar coordinates
$$V_P(r,\theta)=\frac{kq}{\sqrt{r^2-2ra\cos{\theta}+a^2}}-\frac{kq}{r^2+2ra\cos{\theta}+a^2}$$
b) Assume ##r>>a##. Then ##a/r \to 0##. I won't write out the calculations for this approximation. The result is that
$$V_P(r,\theta) \approx \frac{2kqa\cos{\theta}}{r^2}$$
The dipole moment for our dipole is
$$\vec{p}=q\vec{r}_1+(-q)\vec{r}_2$$
$$=2qa\hat{j}$$
Then, we have
$$\vec{p}\cdot \hat{r}=(2qa)\hat{j}\cdot(\sin{\theta}\hat{i}+\cos{\theta}\hat{j})$$
$$=2qa\cos{\theta}$$
and so
$$\vec{p}\cdot \vec{r}k=\frac{2kqa\cos{\theta}}{r^2}=\frac{pk\cos{\theta}}{r^2}$$
Note that this is the same as the potential function at point P, as we wanted to show.
c) To find the polar components of the electric field we simply compute
$$E_{\theta}(r,\theta)=-\frac{1}{r}\frac{\partial}{\partial\theta}V(r,\theta)=\frac{2qka\sin{\theta}}{r^3}=\frac{kp\sin{\theta}}{r^3}$$
$$E_{r}(r,\theta)=-\frac{\partial}{\partial r}V(r,\theta)=\frac{4kqa\cos{\theta}}{r^3}=\frac{2kp\cos{\theta}}{r^3}$$
Finally, we reach part d), which is what this question is about. Here is a depiction
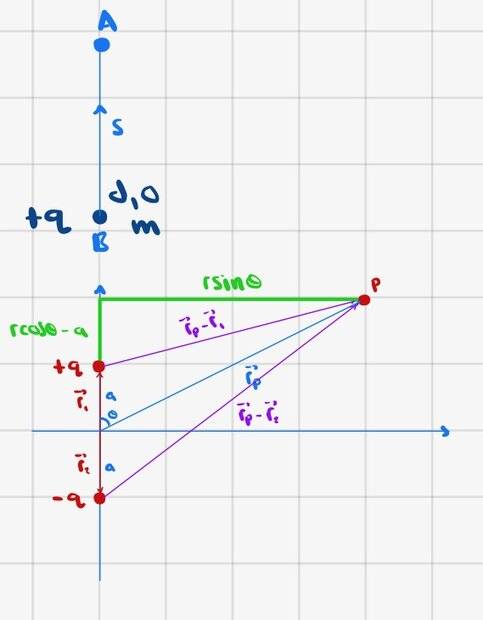
As far as I can tell, the force at any point on the ##y##-axis only has a component in the direction of ##\hat{j}##. Since the charge at B is positive and the closest charge from the dipole is also positive, the charge at point B will accelerate upwards toward point A which in polar coordinates is ##(d+s,0)##.
Previously, we calculated the potential at every point, so we know the potential at ##(d,0)## and ##(d+s,0)##.
The difference in potential ##V_A-V_B## equals the change in potential energy per unit charge between B and A. That is
$$\Delta V=\frac{\Delta U}{q}=\frac{-\Delta K}{q}=\frac{-mv_{final}^2}{2q}$$
Since we know the potentials, and since we know the charge at B is ##+q## and starts at rest, we can compute the change in potential energy of this charge, and that should give us the change in kinetic energy, and thus the final speed.
Is this approach correct?
a) The potential at any point P due to a charge q is given by ##\frac{kq}{r}=\frac{kq}{\lvert \vec{r}_s-\vec{r}_P \rvert}##, where ##r## is the distance from the charge to point P, which is the length of the vector difference between ##\vec{r}_s##, the position of the source charge, and ##\vec{r}_{P}##, the position vector of point P.
Since we have two charges, we compute the potential at a point P using superposition.
Let point P have coordinates ##(x,y)##. Then
$$\vec{r}_1=a\hat{j}$$
$$\vec{r}_2=-a\hat{j}$$
$$\vec{r}_P=x\hat{i}+y\hat{j}$$
$$\lvert \vec{r}_P-\vec{r}_1\rvert = \lvert\langle x,y-a\rangle\rvert=\sqrt{x^2+(y-a)^2}$$
$$\lvert \vec{r}_P-\vec{r}_2\rvert = \lvert\langle x,y+a\rangle\rvert=\sqrt{x^2+(y+a)^2}$$
Thus, by superposition we have
$$V_P(x,y)=\frac{kq}{\sqrt{x^2+(y-a)^2}}+\frac{k(-q)}{\sqrt{x^2+(y+a)^2}}$$
Using
$$x=r\sin{\theta}$$
$$y=r\cos{\theta}$$
we can write ##V_P## in polar coordinates
$$V_P(r,\theta)=\frac{kq}{\sqrt{r^2-2ra\cos{\theta}+a^2}}-\frac{kq}{r^2+2ra\cos{\theta}+a^2}$$
b) Assume ##r>>a##. Then ##a/r \to 0##. I won't write out the calculations for this approximation. The result is that
$$V_P(r,\theta) \approx \frac{2kqa\cos{\theta}}{r^2}$$
The dipole moment for our dipole is
$$\vec{p}=q\vec{r}_1+(-q)\vec{r}_2$$
$$=2qa\hat{j}$$
Then, we have
$$\vec{p}\cdot \hat{r}=(2qa)\hat{j}\cdot(\sin{\theta}\hat{i}+\cos{\theta}\hat{j})$$
$$=2qa\cos{\theta}$$
and so
$$\vec{p}\cdot \vec{r}k=\frac{2kqa\cos{\theta}}{r^2}=\frac{pk\cos{\theta}}{r^2}$$
Note that this is the same as the potential function at point P, as we wanted to show.
c) To find the polar components of the electric field we simply compute
$$E_{\theta}(r,\theta)=-\frac{1}{r}\frac{\partial}{\partial\theta}V(r,\theta)=\frac{2qka\sin{\theta}}{r^3}=\frac{kp\sin{\theta}}{r^3}$$
$$E_{r}(r,\theta)=-\frac{\partial}{\partial r}V(r,\theta)=\frac{4kqa\cos{\theta}}{r^3}=\frac{2kp\cos{\theta}}{r^3}$$
Finally, we reach part d), which is what this question is about. Here is a depiction
As far as I can tell, the force at any point on the ##y##-axis only has a component in the direction of ##\hat{j}##. Since the charge at B is positive and the closest charge from the dipole is also positive, the charge at point B will accelerate upwards toward point A which in polar coordinates is ##(d+s,0)##.
Previously, we calculated the potential at every point, so we know the potential at ##(d,0)## and ##(d+s,0)##.
The difference in potential ##V_A-V_B## equals the change in potential energy per unit charge between B and A. That is
$$\Delta V=\frac{\Delta U}{q}=\frac{-\Delta K}{q}=\frac{-mv_{final}^2}{2q}$$
Since we know the potentials, and since we know the charge at B is ##+q## and starts at rest, we can compute the change in potential energy of this charge, and that should give us the change in kinetic energy, and thus the final speed.
Is this approach correct?