Modelling of two phase flow in packed bed using conservation equations

[casualguitar]

Are you saying you store the results in an output array and write the array to an output file after you are done? If so, why aren't you just writing the results to an output file at each time step?

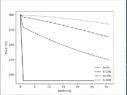
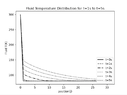
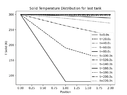
If I understand correctly I'm doing the first option. I'm taking the enthalpy solution array and passing it through the temperature, mass holdup, etc functions to regenerate those values from the enthalpy value

Not efficient I know, however it works and I haven't figured out how to just write the values to an output variable as they are created.

I'm reading the ODE solver documentation currently so I'll aim to change it to the better approach

 

[casualguitar]

You are assuming that the bed temperature and the temperature of the fluid in the bed are initially the same, right?

Right. I think I see what you're saying. I only need one initial condition for the bed - the temperature? I could then just get the enthalpy from the temperature

 

[Chestermiller]

Right. I think I see what you're saying. I only need one initial condition for the bed - the temperature? I could then just get the enthalpy from the temperature

Sure. Isn't that what you did in the 1 tank model?

 

[casualguitar]

Sure. Isn't that what you did in the 1 tank model?

It is, I'm quite stuck on this one though. The functions I made for the previous model used the tank inlet values always (when we had one tank). They were built into the functions. Whereas now we've got to update the $j$ and $j-1$ values. I'm not so fluent with the ODE solver I'm using. I don't know how to do this just yet

 

[casualguitar]

Sure. Isn't that what you did in the 1 tank model?

I think what's confusing me is that I'm trying to include dm/dt in the ODE solver when I don't need to.

Is this statement correct - we are solving for enthalpy at every point at every time step, and every other parameter is known once enthalpy is known $(m,T,\rho,Ts,m_j, \dot{m}_{j-1})$

So really the only point of focus is the enthalpy. Once we know the enthalpy everything else is known through the relations you previously developed

Is the above correct?

 

[Chestermiller]

I think what's confusing me is that I'm trying to include dm/dt in the ODE solver when I don't need to.

Is this statement correct - we are solving for enthalpy at every point at every time step, and every other parameter is known once enthalpy is known $(m,T,\rho,Ts,m_j, \dot{m}_{j-1})$

So really the only point of focus is the enthalpy. Once we know the enthalpy everything else is known through the relations you previously developed

Is the above correct?

Yes. Not only that. Maybe now, with the present sweeping tank-at-a-time setup, it might be easier to do the integration ourselves, without using the package ODE integrator. With an implicit integration like backward Euler or Crank-Nicholson, it would only involve solving two linear equations in two unknowns for each sequential tank for each time step. What do you think?

 

[casualguitar]

Yes. Not only that. Maybe now, with the present sweeping tank-at-a-time setup, it might be easier to do the integration ourselves, without using the package ODE integrator. With an implicit integration like backward Euler or Crank-Nicholson, it would only involve solving two linear equations in two unknowns for each sequential tank for each time step. What do you think?

Hi Chet, just letting you know I am still focusing on the code for this model. I've made some progress and it seems I can do it with the ODE package I previously used. I will continue on with this method for now, as its possible it will be useful in future models

 

[casualguitar]

Yes. Not only that. Maybe now, with the present sweeping tank-at-a-time setup, it might be easier to do the integration ourselves, without using the package ODE integrator. With an implicit integration like backward Euler or Crank-Nicholson, it would only involve solving two linear equations in two unknowns for each sequential tank for each time step. What do you think?

Looks like there's good news on the model. Finishing up my attempt now. Will get some plots in the next hour or so

 

[casualguitar]

Yes. Not only that. Maybe now, with the present sweeping tank-at-a-time setup, it might be easier to do the integration ourselves, without using the package ODE integrator. With an implicit integration like backward Euler or Crank-Nicholson, it would only involve solving two linear equations in two unknowns for each sequential tank for each time step. What do you think?

Hi Chet, the code for the model is done I think. I'm setting up various plots now. Temperature distribution for a number of times here:

The trend seems to look normal to me i.e. the positions closer to the left increase in temperature first, followed gradually by positions closer to the right

 

[casualguitar]

Yes. Not only that. Maybe now, with the present sweeping tank-at-a-time setup, it might be easier to do the integration ourselves, without using the package ODE integrator. With an implicit integration like backward Euler or Crank-Nicholson, it would only involve solving two linear equations in two unknowns for each sequential tank for each time step. What do you think?

And similarly for the fluid enthalpy and mass holdup:

The mass holdup plot isn't exactly visually nice to look at. But yes these are the three plots. How does this look to you?

And the code:

 

[Chestermiller]

And similarly for the fluid enthalpy and mass holdup:
View attachment 293537
View attachment 293538
The mass holdup plot isn't exactly visually nice to look at. But yes these are the three plots. How does this look to you?

And the code:
View attachment 293539
View attachment 293540

This is for 30 tanks, each 1/30 the size of the tank in the single tank model, correct?

In comparison to the single tank model, the time response of this model seems way too fast. The results also seem to show that all the liquid is purged from the bed by 20 sec. This doesn't seem likely. Have you compared the time-dependent results for the first tank in this model with the results of the single tank model for the case of a tank 1/30 the size of the overall bed? The results from this comparison should match.

Also, what does the bed temperature profile look like?

 

[casualguitar]

In comparison to the single tank model, the time response of this model seems way too fast.

Yes I actually forgot to divide the heat transfer area, and the solid mass by the number of tanks when I was making that graph (see Area and mS parameters are not divided by n). I was looking at the effect of having multiple tanks and forgot to switch back. Heres the fluid temperature plot for n = 32. Note that for the first and last timestep Tf == 0. This is because the numerical derivative dH/dt eliminates two data points. So I've manually added in the IC for the fluid (t=0) again for visual purposes:

The solid temperature profile:

Comparing this model with the last one now. I don't think they match though, unless I've compared them incorrectly. Checking now

Also, to confirm - if I divide the volume, area and solid mass by n (number of tanks) at the top of the script when declaring variables, then n will not appear at all further down in the computations?

 

[casualguitar]

Have you compared the time-dependent results for the first tank in this model with the results of the single tank model for the case of a tank 1/30 the size of the overall bed?

Heres the plot of the fluid temperature for the no spatial dependence model.

Thinking about this some more, this graph should roughly match the spatial dependence graph at the first position, which it does

To clarify, I divided the volume, area and solid mass by n = 32 in spatial dependence model (I think I actually should have divided by 30 not 32 but anyway). This means that the first tank in the spatial dependence model, and this non-spatial-dependence model are now identical

 

[Chestermiller]

Yes I actually forgot to divide the heat transfer area, and the solid mass by the number of tanks when I was making that graph (see Area and mS parameters are not divided by n). I was looking at the effect of having multiple tanks and forgot to switch back. Heres the fluid temperature plot for n = 32. Note that for the first and last timestep Tf == 0. This is because the numerical derivative dH/dt eliminates two data points. So I've manually added in the IC for the fluid (t=0) again for visual purposes:
View attachment 293588

The solid temperature profile:
View attachment 293591

Comparing this model with the last one now. I don't think they match though, unless I've compared them incorrectly. Checking now

Also, to confirm - if I divide the volume, area and solid mass by n (number of tanks) at the top of the script when declaring variables, then n will not appear at all further down in the computations?

These times seem very short compared to what was obtained before by the one tank model of the overall bed. Please prepare a comparison plot of the temperature vs time for the 32nd tank vs the corresponding results from the one tank mode of the overall bed. Please comment on any differences. Thanks.

 

[casualguitar]

These times seem very short compared to what was obtained before by the one tank model of the overall bed. Please prepare a comparison plot of the temperature vs time for the 32nd tank vs the corresponding results from the one tank mode of the overall bed. Please comment on any differences. Thanks.

Working on the above now

Would it not be the first tank in the 32 tank model that is comparable to the one tank model, as the ICs and BCs would be the same? As the last tank has a variable inlet mass flow which isn't the case in the single tank model

 

[Chestermiller]

Working on the above now

Would it not be the first tank in the 32 tank model that is comparable to the one tank model, as the ICs and BCs would be the same? As the last tank has a variable inlet mass flow which isn't the case in the single tank model

No. I want to compare what each of the two models predicts for the temperature as a function of time of the gas coming out of the overall bed.

 

[casualguitar]

These times seem very short compared to what was obtained before by the one tank model of the overall bed.

The volume/area/solid mass are smaller (32x smaller) compared to the first iteration of the single tank model. The inlet flowrate is the same as before though, so I think it would be expected to have shorter time scales?

Please prepare a comparison plot of the temperature vs time for the 32nd tank vs the corresponding results from the one tank mode of the overall bed. Please comment on any differences. Thanks.

I can't get the single and 32 tank plots on the same plot, so I'll create two. Here is the single tank model plot, where I have taken the volume area and solid mass we had in the original single tank model, and divided them by n = 32:

So it takes about 2 seconds before the temperature levels off in the single tank

Similarly, for the final tank here is the outlet temperature as a function of time:

So yes the 32 tank model predicts it will take about 80s for the temperature to level out in the final tank (note the time axis shows x1000 currently. This is 0 to 80s). The single tank model predicts it will take 2 seconds for the temperature in the single tank model to level out.

Also the jumps around the 7 to 10s mark are due to the enthalpy function not being continuous. I'm using the enthalpy derivative to calculate the fluid temperatures

Lastly here's the first tank temperature versus time, showing about 30s to level out (also much slower than the single tank model)

Looking into this now

Update: I've got another person to check the newer model and it seems to look ok. Its likely the single tank model that has the error. Checking now

 

[casualguitar]

No. I want to compare what each of the two models predicts for the temperature as a function of time of the gas coming out of the overall bed.

Results for this are in post #192. Is it true to say that there is an error in one of the models because the single tank model temperature profile does not match the first tank in the multi-tank model?
ie.
These are not the same:

I haven't seemed to find any errors in either just yet

 

[Chestermiller]

Results for this are in post #192. Is it true to say that there is an error in one of the models because the single tank model temperature profile does not match the first tank in the multi-tank model?
ie.
These are not the same:
View attachment 293642
View attachment 293643
I haven't seemed to find any errors in either just yet

The Single tank model for the entire bed should match the 32nd tank of the multi tank model. Well what I really mean is that the time scale should match approximately.

 

[casualguitar]

The Single tank model for the entire bed should match the 32nd tank of the multi tank model. Well what I really mean is that the time scale should match approximately.

The time scale of the models further back is much closer to the new spatial variation model, which suggests there is some error in the single tank model, which would seem to make sense anyway as the purge time is very low. Looking into it

 

[casualguitar]

The Single tank model for the entire bed should match the 32nd tank of the multi tank model. Well what I really mean is that the time scale should match approximately.

Getting closer to the solution to this. Its almost definitely got something to do with how I'm adjusting volume, area and solid mass for the single tank model to match the multi tank model values. The reason I think this is because when I fully remove any 'n' from the single tank model i.e. just use the values I used before, the shape of the single and multi tank plots are very similar. Still slightly off in terms of time but they look alike:

Single tank plot:

Multi tank plot:

So when I try to divide by n it fails and I get a plot similar to the very short time scale in a previous post. So it seems that using volume/n, area/n and solidmass/n is not doing what I expected it to do in the single tank plot

Note the times for the multitask plot are x1000 as I haven't figured out how to scale down the x-axis by 1000. The time range here is 0 to 80s

Do these plots 'match'? Or do you reckon there's an error in one?

 

[casualguitar]

Edit: The above plots are of time versus enthalpy (forgot to change the y-axis label)

Here are the plots of fluid temperature versus time for both cases:

1) The single tank model:

Last tank in the 32 tank model (where actual t = t/1000):

These plots seem to show a similar trend and an approximately equal 'levelling off' time for the fluid temperature. The fix (if you agree these plots look ok) was in how I was dividing up the volume, area, and solid mass per unit area

I am absolutely ready to work some more on this model today if you think we're ready to do some more

 

[Chestermiller]

Getting closer to the solution to this. Its almost definitely got something to do with how I'm adjusting volume, area and solid mass for the single tank model to match the multi tank model values. The reason I think this is because when I fully remove any 'n' from the single tank model i.e. just use the values I used before, the shape of the single and multi tank plots are very similar. Still slightly off in terms of time but they look alike:

Single tank plot:
View attachment 293646
Multi tank plot:
View attachment 293648
So when I try to divide by n it fails and I get a plot similar to the very short time scale in a previous post. So it seems that using volume/n, area/n and solidmass/n is not doing what I expected it to do in the single tank plot

Note the times for the multitask plot are x1000 as I haven't figured out how to scale down the x-axis by 1000. The time range here is 0 to 80s

Do these plots 'match'? Or do you reckon there's an error in one?

They have to approximately match on the time scale. The multi-tank time variation of the temperature leaving the tank should be sharper (closer to a square wave) than the single tank model of the overall bed. But they need to be close to one another. The multi-tank should have lower temperatures at short times and higher temperatures at longer times; so they have to cross over one another.

The time scale for the response should be roughly on the order of $$\frac{m_SC_S}{UA}$$What value do you calculate for this?

I'm going to try to leave the coding up to you and only offer guidance on model structure.

 

[casualguitar]

The time scale for the response should be roughly on the order of mSCSUAWhat value do you calculate for this?

11 for this ($mS = 1, C_ps = 1.1, U = 1, A = 0.1$). Is this time scale term an approximation for the time it should take to reach steady state in a tank?

The multi-tank time variation of the temperature leaving the tank should be sharper (closer to a square wave) than the single tank model of the overall bed.

Ok so are you saying there is an error in the multi-tank model because it doesn't really cross over the single tank model at all? i.e. higher temperature at low and high times

I'm going to try to leave the coding up to you and only offer guidance on model structure.

Thats good with me, I don't think the code will get much more complex math-wise than it is currently anyway

 

[Chestermiller]

11 for this ($mS = 1, C_ps = 1.1, U = 1, A = 0.1$). Is this time scale term an approximation for the time it should take to reach steady state in a tank?

For the bed

Ok so are you saying there is an error in the multi-tank model because it doesn't really cross over the single tank model at all? i.e. higher temperature at low and high times

I don’t know which model has the error (or errors). This is part of doing the validation of the model.

 

[casualguitar]

For the bed

I don’t know which model has the error (or errors). This is part of doing the validation of the model.

Got it my bad working on this now.

One approach to do this could be to reduce to 3 tanks and do some manual calculations to see which model values don't match the manually calculated versions. Trying this now

 

[Chestermiller]

What were the units of that approximate time scale calculation?

 

[casualguitar]

What were the units of that approximate time scale calculation?

$\frac{kg*\frac{kJ}{kgK}}{\frac{W}{m2K}*m2}$ = $\frac{kJ}{W}$ = $1000*s$ == kilo seconds I suppose?

Changing the heat capacity units to $\frac{J}{kgK}$ gives a value of 11,000s for the time scale of the response

 

[Chestermiller]

$\frac{kg*\frac{kJ}{kgK}}{\frac{W}{m2K}*m2}$ = $\frac{kJ}{W}$ = $1000*s$ == kilo seconds I suppose?

Changing the heat capacity units to $\frac{J}{kgK}$ gives a value of 11,000s for the time scale of the response

You got to be kidding. Changing the units of heat capacity doesn’t change the value of this quantity. The result is still 1100 sec.

 

[casualguitar]

You got to be kidding. Changing the units of heat capacity doesn’t change the value of this quantity. The result is still 1100 sec.

Ah no I agree it doesn't change the value, just the unit of time i.e. from kilo seconds to seconds. My original value of 11 was in kilo seconds (according to the above). Multiplying by 1000 to convert to seconds. Is this incorrect?

Apologies for the confusion here. I think it might be best for me to spend some time looking at the output of the spatial variation model (and doing some manual calculations to check the model output). Otherwise I'm wasting your time and mine

 

[Chestermiller]

1100 is correct

 

[casualguitar]

1100 is correct

So 1100s is the approx time it would take for the solid temperature to reach steady state i.e. the timescale. The solid temperature will converge exponentially towards 300 but will never reach 300. Where would the cut-off point be here? Say within 0.1K or so? I can check the exact time required for the cutoff to be reached.

 

[Chestermiller]

So 1100s is the approx time it would take for the solid temperature to reach steady state i.e. the timescale. The solid temperature will converge exponentially towards 300 but will never reach 300. Where would the cut-off point be here? Say within 0.1K or so? I can check the exact time required for the cutoff to be reached.

We have got to take a step back, and make sure that the single tank model of the entire bed is getting the right answer. This can be checked by running a calculation in which the model can be solved analytically. Such a case would be if the stream entering the tank is a liquid at a temperature below the saturation temperature, and the bed is initially at a colder temperature. Then we can compare the analytic solution to the time-dependent numerical solution to make sure that the time scale we get numerically is correct.

After that, I have developed an even simpler version of the multi-tank model that is easier to implement, and less prone to coding error. I have shown that the multi-tank model is equivalent to n tanks in series identical in every respect to that being used in the single tank model of the entire bed, but with a mass flow to the first tank in the series equal to n times the actual mass flow rate to the actual bed. I will document the new development once we have validated the single tank model.

 

[casualguitar]

We have got to take a step back, and make sure that the single tank model of the entire bed is getting the right answer. This can be checked by running a calculation in which the model can be solved analytically. Such a case would be if the stream entering the tank is a liquid at a temperature below the saturation temperature, and the bed is initially at a colder temperature. Then we can compare the analytic solution to the time-dependent numerical solution to make sure that the time scale we get numerically is correct.

Great! I follow the first paragraph idea. So focusing on the first paragraph - we will have $h<=0$ at all times, meaning we can use the liquid correlations for temperature and mass holdup i.e. $T = T_{SAT} + \frac{h}{C_{PL}}$ and $m = \rho_{L}*V$.

Letting Tsat = 105, Tin = 90, and T0 = 80 (bed/fluid initial temperature), for the single tank model, this is the plot for the liquid phase only model:

If we are expecting a timescale of 1100s here this seems to line up relatively ok.

I did the same for gas phase only - where Tsat = 105, Tin = 300 and T0 = 200 (bed/fluid initial temperature), for the single tank model. Gas phase plot looks like this:

Seems to look off, due to that fluid temperature jump at the start. Will do some diagnostic testing on the gas phase section

 

[Chestermiller]

Great! I follow the first paragraph idea. So focusing on the first paragraph - we will have $h<=0$ at all times, meaning we can use the liquid correlations for temperature and mass holdup i.e. $T = T_{SAT} + \frac{h}{C_{PL}}$ and $m = \rho_{L}*V$.

Letting Tsat = 105, Tin = 90, and T0 = 80 (bed/fluid initial temperature), for the single tank model, this is the plot for the liquid phase only model:View attachment 293726
If we are expecting a timescale of 1100s here this seems to line up relatively ok.

I did the same for gas phase only - where Tsat = 105, Tin = 300 and T0 = 200 (bed/fluid initial temperature), for the single tank model. Gas phase plot looks like this:
View attachment 293728
Seems to look off, due to that fluid temperature jump at the start. Will do some diagnostic testing on the gas phase section

Do you know how to solve this analytically (two linear coupled ODEs in two unknowns)?