Moving a box on an inclined plane. Find F(min), angle and W(min)

[Michael_0039]

Homework Statement

Moving a box on an inclined plane. friction coefficient is f. We pull the box with angular force (pic below) Which is the angle θ where the F is minimum. Find the Fmin and the Work of Fmin. when the box is on height H

Relevant Equations

nill

Hi,

this is my try:

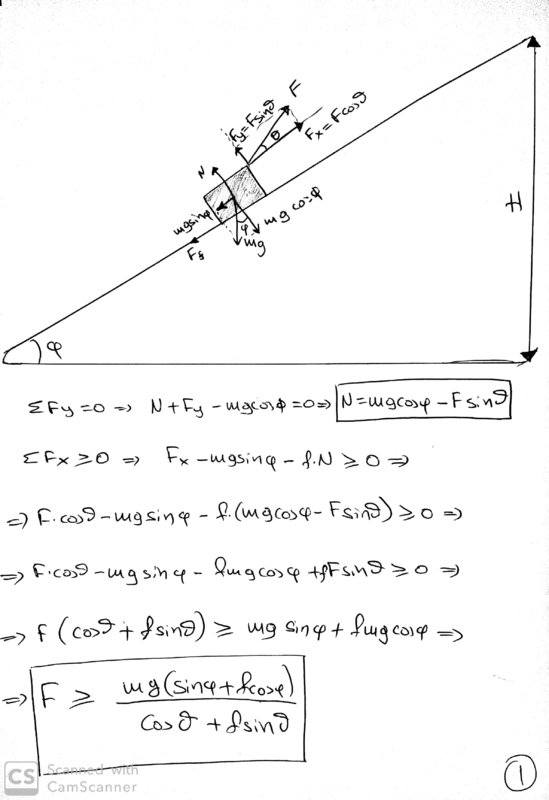
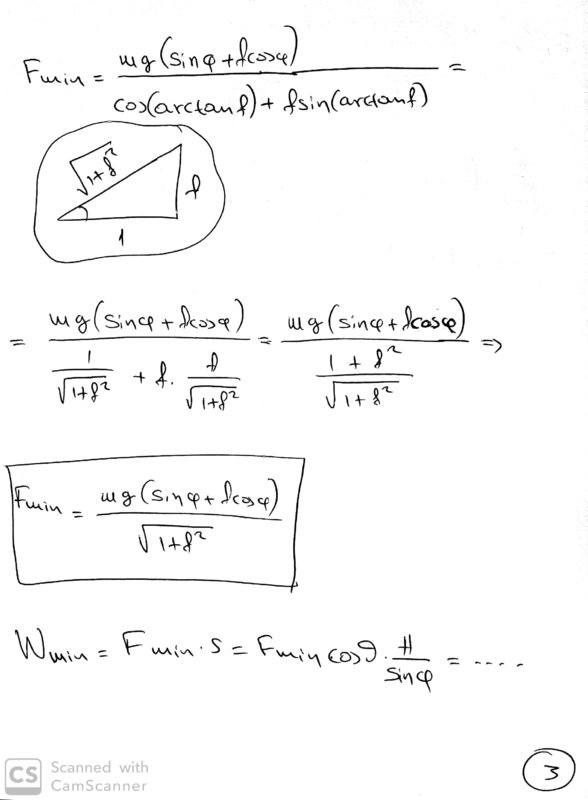
I would appreciate any confirmation or correction .

--
Thanks

 

[PeroK]

All looks good to me.