Network Maximum Power Transfer Calculation

Click For Summary

Discussion Overview

The discussion revolves around calculating the load impedance for maximum power transfer in a given electrical network, utilizing Thevenin's theorem. Participants explore the implications of frequency on impedance and the application of the Maximum Power Transfer Theorem (MPTT) in the context of AC circuits.

Discussion Character

  • Homework-related
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant questions whether a given value labeled as E in the problem statement is a printing error, suggesting it should be in volts rather than hertz.
  • Another participant clarifies that impedance depends on frequency, not voltage, and provides the formula for angular frequency.
  • Calculations for Thevenin impedance are presented, with one participant providing specific resistance values and calculations.
  • Concerns are raised about the imaginary component of inductance, with a participant emphasizing the need to consider complex impedance.
  • Participants discuss the application of the MPTT, with some asserting that the load impedance should equal the Thevenin impedance, while others argue that it involves the complex conjugate of the source impedance.
  • Frustration is expressed by some participants regarding the complexity of the problem and the lack of examples that match their specific circuit configuration.
  • There is a suggestion to assume a unit voltage source for simplification, which some participants find confusing.

Areas of Agreement / Disagreement

Participants express various viewpoints on the application of the MPTT, particularly regarding the relationship between load impedance and Thevenin impedance. There is no consensus on the correct approach or interpretation of the problem, and multiple competing views remain throughout the discussion.

Contextual Notes

Participants note the complexity of deriving the MPTT for complex impedances compared to real-valued resistances. There is also mention of the challenge posed by the lack of a specified voltage source in the problem, which complicates the calculations.

Who May Find This Useful

This discussion may be useful for students and individuals studying electrical engineering concepts, particularly those focusing on circuit analysis, Thevenin's theorem, and the Maximum Power Transfer Theorem in AC circuits.

  • #31
Thanks.And sorry for wasting your time
 
Physics news on Phys.org
  • #32
shaltera said:
Thanks.And sorry for wasting your time

You're welcome. No worries, glad to help (or at least try :smile:) If you want to continue or try again, we'll be here.
 
  • #33
Thanks.This problem is already solved.:devil:.
 
Last edited:
  • #34
gneill said:
Your circuit also has a voltage source. It's an AC voltage source, only they haven't specified a particular voltage; they've just supplied the frequency of the AC source. The frequency is the important piece of information for this problem since it determines the impedance of any reactive components (inductors or capacitors). You can assume a 1V AC source if you wish.

While the total power depends on the voltage, the fraction of the total that ends up in the load depends upon the source impedance (your Thevenin equivalent) and the load impedance. The source voltage is just a scaling factor. The frequency determines the impedances, and so determines how the power will be split between the source impedance and load impedance.

What do you me by to "assume a 1V AC source"?

Eth=1V?
 
  • #35
shaltera said:
What do you me by to "assume a 1V AC source"?

Eth=1V?

Sure. 1 V @ 50 Hz would do nicely.

If a particular value is not critical to the details of the analysis, it's generally simplest to assume a unit quantity.
 
  • #36
All examples I found on the internet are with a load resistance Rl,resistors and voltage
 
  • #37
shaltera said:
All examples I found on the internet are with a load resistance Rl,resistors and voltage

What sort of examples are you looking for? Worked problems?
 
  • #38
Similar circuit.What confuses me is that there is no Voltage source and between A-B is not resistor so I can't calculate Rl.This circuit diagram looks to me like an open circuit.Not to forget this 700mH inductor.
 
  • #39
shaltera said:
Similar circuit.What confuses me is that there is no Voltage source and between A-B is not resistor so I can't calculate Rl.This circuit diagram looks to me like an open circuit.Not to forget this 700mH inductor.

There is a voltages source: A 50 Hz AC voltage source. You can assume any value for the voltage you wish, it will not affect the results.

The inductor just contributes to the impedance attributed to the supply network. Once you reduce the supply network to its Thevenin equivalent as seen from terminals A-B the circuit then looks just like the archetypal "maximum power transfer circuit where you are to stick some impedance on A-B to serve as the load.
 
  • #40
I have no problem to understand this circuit diagram, and find the Zl?
But with Zth I don not get it,sorry

ZTH4.jpg
 
Last edited:
  • #41
That's why I directed you to the Wikipedia article. It has a relatively clear derivation of the result where the R's are instead impedances.

One way to grasp the reason for the result found is that reactances do not consume real power. They store and return it (a capacitor charges, storing up energy (1/2)CV2 on one half of the cycle, but return that same power to the source on the discharge half of the cycle. The same goes for inductors) The power that accomplishes this, while not lost, is not consumed by the load, and the source still has to be able to provide and recover it on every cycle.

So the way to avoid this waste is to choose the reactive part of the load impedance so that when added to the source impedance the net result is purely resistive. Then you're left with just the source resistance and load resistance to deal with, which is the case solved in your post (I see you've changed that. Oh well...).
 
Last edited:
  • #42
The power dissipated should end up being a real value only. Imaginary power is not dissipated by loads.

You still have not taken in the conclusion of the derivation shown on the Wikipedia page!

You correctly calculated the source impedance in post #8. The required load impedance can be written by inspection from that value. Look again at the last line of the derivation on the Wikipedia page. It tells you how to write the load impedance from the source impedance; they are complex conjugates.

The answer you supply for the actual power dissipated should be a real value, and it should leave the source voltage in symbolic form ("E").
 
  • Like
Likes   Reactions: 1 person
  • #43
I= Vs / Zs+Zl
Zl=Rl+jXl
P=I2Rl

Zs=Rs+jXs=Rl-jXl
 
  • #44
shaltera said:
I= Vs / Zs+Zl
Zl=Rl+jXl
P=I2Rl

Zs=Rs+jXs=Rl-jXl

Okay, can you put numbers to the variables that you have values for?
 
  • #45
C=1/(\omegaXc)
 
Last edited:
  • #46
I managed to calculate Ze and Zl

Ze=(330.3+j219.8)ohms
Hence Zl=(330.3-j219.8)
C=1(314x219.8)=14.49mF

14.49mF is the power I believe
 
  • #47
shaltera said:
I managed to calculate Ze and Zl

Ze=(330.3+j219.8)ohms
Hence Zl=(330.3-j219.8)
C=1(314x219.8)=14.49mF

14.49mF is the power I believe

mF is capacitance. That's the equivalent capacitance that the load impedance presents. The unit of power is the watt. You'll have to find the power dissipated by the resistive part of the load impedance.

Since you weren't given a particular value for the source voltage your result will be an expression rather than a numeric value. Give the source voltage a name, say E. Now, knowing all the rest of the component values for the circuit you can determine the currents and potentials in terms of E.

Hints:
1. You've determined the Thevenin impedance for the source. Determine also the Thevenin voltage Eth in terms of E.
2. With the Thevenin equivalent in place and the load impedance connected you have a series circuit. Determine the net impedance that the Thevenin source "sees".
 
  • #48
Rl=Re[Zth] and Xl=Im[Zth]

Pmax=Vth2/4Re[Zth]
 
  • #49
shaltera said:
Rl=Re[Zth] and Xl=Im[Zth]

Pmax=Vth2/4Re[Zth]

Yes. But you can simplify it further by plugging in the known value of Re(Zth) and an expression for Vth in terms of E. You should end up with an expression of the form c1E2 or E2/c2, where the c's are some constants.
 
  • #50
Zth=330.3+j219.8

Pmax=1V2/4(330.3-J219.8) ?
 
  • #51
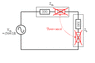
shaltera said:
Zth=330.3+j219.8

Pmax=1V2/4(330.3-J219.8) ?

There should be no imaginary values in the consumed power. Consumed power is a real quantity. What did you get for your Thevenin voltage? (it should be an expression containing the variable E, which is the unknown source voltage).
 
  • #52
e=(V1xZ2)/Z1+Z2

But I don't have a source voltage, just a frequency of 50Hz which I used to calculate Xl?

OK if I assume that my source has avoltage of 1V,then e=1000/1220=1.2V (th voltage)

Pmax=1.22/(330.3+j219.8)
 
Last edited:
  • #53
shaltera said:
e=(V1xZ2)/Z1+Z2

But I don't have a source voltage, just a frequency of 50Hz which I used to calculate Xl?

OK if I assume that my source has avoltage of 1V,then e=1000/1220=1.2V (th voltage)

Pmax=1.22/(330.3+j219.8)

Just let the source voltage be the symbol "E". Then your Thevenin voltage is (1000/1220)E.

Now, what impedance does this Thevenin voltage "see" when the circuit is complete?
 
  • #54
I'm not sure.Is it Z2?
 
  • #55
Draw the circuit --- components are Vth, Zth, ZL. Plug in the values of Zth and ZL. What is Vth "seeing"?
 
  • #56
What's the net equivalent impedance?
 
  • #57
Zth?
 
  • #58
shaltera said:
Zth?

What is Zth? What is the load impedance ZL? How are they connected in the circuit? What then is the net impedance?
 
  • #59
Zeq=Zl(Vl/Vs-1)
 
  • #60
shaltera said:
Zeq=Zl(Vl/Vs-1)

There are no voltages in an impedance. You have two impedances: Zth and ZL. What are they (you spent much time calculating them!)?
 

Similar threads

Using the maximum power transfer theorem
  • · Replies 1 ·
Replies
1
Views
3K
Maximum power is transferred when load R = Source R ?
  • · Replies 13 ·
Replies
13
Views
2K
Maximum Power Transfer Ideal Transformer
  • · Replies 6 ·
Replies
6
Views
3K
Engineering Maximum power transfer in a circuit
  • · Replies 1 ·
Replies
1
Views
4K
What is the Maximum Power Transfer Theorem?
  • · Replies 5 ·
Replies
5
Views
2K
Engineering Thevenin equivalent of circuit and maximum power transfer
  • · Replies 2 ·
Replies
2
Views
2K
Max Power Transfer Homework: Find Ro for Max Power
  • · Replies 7 ·
Replies
7
Views
2K
How to maximum apparent power through a linear transformer?
  • · Replies 8 ·
Replies
8
Views
2K
Engineering Understanding Maximum Power in Circuit: Comparing Load and Circuit Approaches
  • · Replies 7 ·
Replies
7
Views
3K
Engineering Calculate the maximum power of the resistor in a circuit
  • · Replies 8 ·
Replies
8
Views
3K