Perspective on Relativity and Length Contraction

[phyti]

the muon scenario for anyone's consideration (without all the fluff)

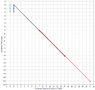
In the left figure, the Earth observer E records the avg. travel time of the muon for the distance x (altitude to ground) as t. E calculates the travel time for M the observer moving with the muon as t', resulting from time dilation. M's clock shows t' at the ground, yet his position is x. He calculates his position should be vt' = x'. Since M experiences time dilation to the same degree as his clock, his sense of time agrees with his clock. To reconcile the distance disparity, he concludes the universe outside his frame of reference has contracted in the x direction, as shown in the right figure.

If time dilation and length contraction are motion induced phenomena, then
this large scale length contraction is not a consequence of em field deformation, but the interpretation of the observers own time dilation. The observer's motion cannot alter the form of distant objects, but can alter his perception.

 

[TheBC]

Ghwellsjr, thanks for again putting so much effort in discussing diagrams.

I do not agree with you that the simultaneous green car events are 'really' 'physically' out there.

Then please tell me which events of the short green car are out there for Red between his red hands. (Definitely not the green rest car events!)

The simultaneity of the green car events are frame variant. Same with the red car events. Simultaneity is a coordinate effect.

I'm asking you: which events of the short green train are between the red hands of the observer? The events of the green rest train? No. So, which events are between his hands? Please tell me.
I don't like at all you call it an 'effect'. The frame (any frame) indicates which events out of 4D spacetime existence form a 3D space of simultaneous event, i.o.w. the 3D world as it 'exists' at one moment in time.
You will tell me that that 3D world is 'arbitrarily 'chosen... I don't care less. Point is that an observer considers some events frome 4D spacetime as his 'real world now'. And because of relativity of simultaneity green's 3D world is different from red's 3D world. The content of events is completely different. The only invariant in this exercise is the full picture: all the 4D spacetime events, the 4D spacetime world.

Only the first diagram is "as seen from the railway track".

I cannot see this. For me it's what red measures. In your first diagram I read that horizontally you give length12 for red car at rest and length 6 for short green car.

Then I don't see why you would think a Loedel diagram is relevant for reciprocal length contraction.

Because Loedel shows you in one diagram the same proper rest length in both frames.
What is astonishing is that apparently you use your 3 rd diagram for other purposes that I would do. Because in no time I make it a loedel diagram. Your 3 rd diagram with coordinate distances is about a frame I am not interrested in. Because you don't show any of the 12 proper length or 6 long contracted cars in your 3 rd diagram. But the information is in your drawing, so why not showing it? Drop your irrelevant horizontal and vertical margins and read directly what red and green measure in their respective 3D space. Piece of cake. In next post I will mark up your diagram so it can be read as loedel.

Then I transformed the first chart to a speed of 57.7%c which is the speed at which both trains are traveling at the same speed.

I don't need this. Both cars are traveling relative to each other at same speed (0;866c). I don't need anything else.

And why should you? Since both trains are traveling at the same speed, they are contracted to the same length. There's nothing sacrosanct about the length of 6 feet. You only get a contraction to 50% of the Proper Length of 12 feet when the speed is 86.6%c. Since these trains are traveling at 57.7%c, they are contracted to 1/1.22 or just under 10 feet as the diagram shows.

I don't need the 57.7%c. Once more: it's about reciprocal length contraction between the 2 cars. They are traveling at 86.6%c relative to each other. And that's all I need.
Your first diagram shows red's frame: a 12 long red car for red observer and a 6 long green car.
Your second chart shows green's frame: 12 long green car for green observer and a 6 long red car.
Your 3 rd diagram is a loedel diagram only if you also indicate the green and red frames in which you read proper and contracted lengths on both axes with one and same ruler.

That's because you are adding the coordinates from two other frames to the original frame. Nothing wrong with that, as long as your audience understands how to read the diagram. If the two added sets of coordinates are not drawn on the diagram, then it becomes very difficult to understand how to read it.

I never said is is 'easy' to read. But let's be honnest; do you find a Minkoski diagram, with different unit lengths for time and space 'easy' to read reciprocal length contraction and time dilation? Forget it.
I find loedel A LOT easier to read than your or Minkowski... But it has it's limitations. More than 2 frames f.ex. Because then not all frames keep same unit lenghts...
But for most exercises where only two relative moving systems are used loedel is sublime.

I just prefer separate clearly marked diagrams.

This is where we disagree. Dalespam too does not see any advantage of one loedel over 2 separate diagrams because it does not show more raw date than your two diagrams. In that sense raw data written on a piece of paper, cut to pieces and thrown on the floor also 'contains' all the information. But Loedel shows clearly how all rest and shorter 'moving' length are part of one full 4D spacetime diagram. With one ruler.

But you can easily calculate it using the formula for the spacetime interval.

There we are. With loedel you do not have to calculate it. You just measure it all with one and the same ruler. And believe it or not, it's on your diagram but apparently you are not aware of it.

As I see it, the Proper Length between A and C is the distance between red's fingertips (6 feet) in the first diagram. I don't know where you got the 12 from.

(In first diagram) Then what represents the distance between your two vertical red lines of the red car (at rest for red)?

And E-G is the proper length between green's fingertips, not the green train in the second diagram.

Correct. Sorry about that. My mistake.

I thought I did what you wanted. Did you see the line segments A-D-C and E-H-G? Maybe you're looking at it on a small screen.

I saw them full scale, but they are not what I asked.
Once more: quote<<Draw on the diagram the light paths from the rear and front of the green rest train and see where they end at red's head. That's a complete different story, irrelevant for red's measurement of a shorter green train.>>
In fact you should draw a line between E-G en continue to the green worldlines of the front and rear of green car. The line is 'made of'/represents all the events that are simultaneous for green at one moment of time on green's wristwatch.
Similar reasoning for red. That red line is 'made of'/represents all the events that are simultanoeus for red.
Dalespam may call this this clutter, but I find this essential to understand 4D of SR.
See my comments to his quote:

The only possible addition is to label the two moving frame's axes. Personally, I think that would just add clutter,

You call that clutter? Waw! Interesting. I rather call the extra frame in which both cars have equal contracted length completely obsolete. Totally irrelevant for reciprocal length contraction.

but I think that is what he considers to be missing.

That's indeed a good start.

 

[TheBC]

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

 

[nitsuj]

Love the Festive coloring!

 

[PAllen]

Love the Festive coloring!

Yep, a SAD case (Seasonally Appropriate Diagram)

 

[pervect]

Very christmassy, but unfortunately I can't tell what it's supposed to represent.

I guess the vertical axis is some coordinate time t, and the horizontal axis is some coordinate position x. There's some grey lines through the labels, but I can sort of make out the text anyway. I don't understand the motivation for the wiggly grey lines.

Then the red car apparently at t=2 was at x=4, and at t=3 was at x=-5.5.

If we assume c=1, this would be FTL. Presumably c then has some other value than 1.

are the thin diagonal lines supposed to be "lightcones"? Hard to say, but if so, then I guess c is supposed to be near 2, but it doesn't seem to be exactly. Perhaps this choice was explained in some post in the thread I didn't read, but it seems like a strange choice. Why not make c=1? Or at least tell us what it is.

"Space-time existence" isn't a familiar standard term, I don't know what the author is trying to imply by it. It looks like it may be a future light cone for the green line, and a past lightcone for the red line? It seems to have philosophical overtones, rather than being a statement of where the coordinate chart is valid.

 

[ghwellsjr]

Ghwellsjr, thanks for again putting so much effort in discussing diagrams.

You're welcome.

I do not agree with you that the simultaneous green car events are 'really' 'physically' out there.

Then please tell me which events of the short green car are out there for Red between his red hands. (Definitely not the green rest car events!)

Just to make it clear, my issue with you is characterizing the simultaneity of certain events as 'really' 'physically' out there.

But to answer your question: one of the events is labeled "A" in my three diagrams and the other one is labeled "C". In each diagram, the event labeled "A" is the same event. It has different coordinates in each diagram and once we know the coordinates in one diagram, the Lorentz Transformation process is how we determine what the coordinates for the same event are in another diagram. The event occurs 'really' and 'physically' out there when the "left" end of the green car becomes coincident with red's "left" fingertip. The coordinates that we apply to this event are totally arbitrary and do not have the attributes of 'really' or 'physically'.

Similar comments for event "C".

Thus, if it happens in a particular Inertial Reference Frame that they have the same time coordinate, then we say that they are simultaneous in that IRF. Events "A" and "C" have the same time coordinate in my first diagram and are therefore simultaneous in that IRF. In the other two IRFs depicted in the other two diagrams, events "A" and "C" have different time coordinates and are not simultaneous.

As far as I know, the foregoing is mainstream Special Relativity. I don't think it is just my opinion. If you don't accept it, then I don't think you are accepting mainstream Special Relativity.

The simultaneity of the green car events are frame variant. Same with the red car events. Simultaneity is a coordinate effect.

I'm asking you: which events of the short green train are between the red hands of the observer? The events of the green rest train? No. So, which events are between his hands? Please tell me.

In the second frame depicted in the second diagram, it is the same events labeled "A" and "C" which are also on the ends of the green rest train, or, as I prefer to say it, it is the frame in which the green train is at rest, or it is the green train's rest frame.

I don't like at all you call it an 'effect'. The frame (any frame) indicates which events out of 4D spacetime existence form a 3D space of simultaneous event, i.o.w. the 3D world as it 'exists' at one moment in time.
You will tell me that that 3D world is 'arbitrarily 'chosen... I don't care less. Point is that an observer considers some events frome 4D spacetime as his 'real world now'. And because of relativity of simultaneity green's 3D world is different from red's 3D world.

I think the problem is that you consider an observer in a scenario to be locked into one particular frame, namely the frame in which he is at rest. I'm trying to point out that there is nothing that this observer can measure, observe or see that will force him to that conclusion. He must apply Einstein's simultaneity convention, which is what your red and green observers did in your scenario to arrive at the conclusion that what they felt on their fingertips occurred simultaneously. There's no dispute on that issue. What is in dispute is that Einstein's simultaneity convention is real and physical. In other words, two events are only simultaneous because we define them to be simultaneous. It is not a physical thing that we could let nature (the physical world) decide for us or that we could discover by only measurements or observations.

The content of events is completely different. The only invariant in this exercise is the full picture: all the 4D spacetime events, the 4D spacetime world.

I don't know what you mean by this. What is the content of an event? The closest thing I can think of is its coordinates but you don't seem to be to appreciative of coordinates so I'm wondering if you mean that some events belong exclusively to a particular object and some other events belong exclusively to another (and some other events can belong to both objects). Is that what you mean, or something like that?

Only the first diagram is "as seen from the railway track".

I cannot see this. For me it's what red measures. In your first diagram I read that horizontally you give length12 for red car at rest and length 6 for short green car.

Yes, the grid lines going to the coordinate markings tell you that. Since the red car is at rest on the railway track and both are at rest in this IRF, we can say it is "as seen from the railway track". Those are your words. I would rather say that it is the mutual rest frame of the railway track and the red car because neither the railway track (or any observers stationed along it) nor the red car (or any observers stationed within it) can actually see most of the details that we can see when we look at the completed diagram. Of course, as I have repeatedly said, they can construct those details by sending and receiving radar signals and images from remote objects and applying Einstein's convention and doing a lot of calculations after the scenario is all done.

Then I don't see why you would think a Loedel diagram is relevant for reciprocal length contraction.

Because Loedel shows you in one diagram the same proper rest length in both frames.
What is astonishing is that apparently you use your 3 rd diagram for other purposes that I would do. Because in no time I make it a loedel diagram. Your 3 rd diagram with coordinate distances is about a frame I am not interrested in. Because you don't show any of the 12 proper length or 6 long contracted cars in your 3 rd diagram. But the information is in your drawing, so why not showing it? Drop your irrelevant horizontal and vertical margins and read directly what red and green measure in their respective 3D space. Piece of cake. In next post I will mark up your diagram so it can be read as loedel.

I never said it was a Loedel diagram. I only provided the third diagram as a basis for making a Loedel diagram. Remember, I said that a Loedel diagram depicts three frames on the same diagram--all three of my diagrams get squeezed on to the one diagram by providing additional grid lines and markings--if you want to make it clear. As the wikipedia article says:

...there is a frame of reference between the resting and moving ones where their symmetry would be apparent. Such a frame of reference is a Loedel frame. In this frame, the two other frames are moving in opposite directions with equal speed.

Count them: there are three frames jammed into one diagram. I show all three frames as separate diagrams because it is so much easier to read and in this day of computers, they are so easy to generate. My problem with the Loedel diagram is providing the three sets of grid lines and three sets of markings. Since you leave them all out, I don't know how you can tell what is going on.

Then I transformed the first chart to a speed of 57.7%c which is the speed at which both trains are traveling at the same speed.

I don't need this. Both cars are traveling relative to each other at same speed (0;866c). I don't need anything else.

I can easily see that each car is traveling at 57.7%c relative to the coordinates of the frame but how can you tell that each car is traveling at 0.866c relative to the other car?

And why should you? Since both trains are traveling at the same speed, they are contracted to the same length. There's nothing sacrosanct about the length of 6 feet. You only get a contraction to 50% of the Proper Length of 12 feet when the speed is 86.6%c. Since these trains are traveling at 57.7%c, they are contracted to 1/1.22 or just under 10 feet as the diagram shows.

I don't need the 57.7%c. Once more: it's about reciprocal length contraction between the 2 cars. They are traveling at 86.6%c relative to each other. And that's all I need.
Your first diagram shows red's frame: a 12 long red car for red observer and a 6 long green car.
Your second chart shows green's frame: 12 long green car for green observer and a 6 long red car.
Your 3 rd diagram is a loedel diagram only if you also indicate the green and red frames in which you read proper and contracted lengths on both axes with one and same ruler.

I agree, if you transformed the grid lines for the first two diagrams so that you could actually indicate the 12-foot Proper Length of each car and the 6-foot Contracted Length from the other car's rest frame but instead, you have a magic ruler. How do you "calibrate" this ruler? How do you know how to lay it on the diagram to get the measurements. Do the red and green observers have access to this ruler?

That's because you are adding the coordinates from two other frames to the original frame. Nothing wrong with that, as long as your audience understands how to read the diagram. If the two added sets of coordinates are not drawn on the diagram, then it becomes very difficult to understand how to read it.

I never said is is 'easy' to read. But let's be honnest; do you find a Minkoski diagram, with different unit lengths for time and space 'easy' to read reciprocal length contraction and time dilation? Forget it.

No, I don't find the typical Minkowski diagram, with or without grids and markings easy to read. But I understand their historical significance--and Loedel diagrams--because it was fairly difficult to make any diagram by hand but with our computers, it is easy to make interactive diagrams where the user can "dial" in any speed he wants to see how the Lorentz Transformation process creates additional IRF's.

I find loedel A LOT easier to read than your or Minkowski... But it has it's limitations. More than 2 frames f.ex. Because then not all frames keep same unit lenghts...
But for most exercises where only two relative moving systems are used loedel is sublime.

That's only one exercise. Two inertial observers. It can't even show the most popular of all scenarios, the Twin Paradox. My diagrams are trivially easy to read (as you have already demonstrated) and can be used with any in-line scenario. And I can even expand to non-inertial frames using the exact same techniques that observers can use to construct Inertial Reference Frames. They are truly sublime.

But I don't object to a properly drawn and marked Loedel diagram with enough explanation to make its interpretation clear. I do object to the idea that it conveys anything more than any other properly drawn diagram.

I just prefer separate clearly marked diagrams.

This is where we disagree. Dalespam too does not see any advantage of one loedel over 2 separate diagrams because it does not show more raw date than your two diagrams. In that sense raw data written on a piece of paper, cut to pieces and thrown on the floor also 'contains' all the information. But Loedel shows clearly how all rest and shorter 'moving' length are part of one full 4D spacetime diagram. With one ruler.

Again, you are giving preference to each observer's rest frame and concluding that both are in operation at the same time and ignoring the fact that any other frame is just as valid.

But you can easily calculate it using the formula for the spacetime interval.

There we are. With loedel you do not have to calculate it. You just measure it all with one and the same ruler. And believe it or not, it's on your diagram but apparently you are not aware of it.

I'm not aware of where you got the 12-foot length of the ruler that you can place in just the right spot to measure both the Proper Length of one car and the Contracted Length of the other car. How do you determine that it's 12 feet long and not 8? Where do you get the information from that it is 12? And how do you know what angle to draw the two sets of lines at? And where do you show the relative speed between the two observers?

As I see it, the Proper Length between A and C is the distance between red's fingertips (6 feet) in the first diagram. I don't know where you got the 12 from.

(In first diagram) Then what represents the distance between your two vertical red lines of the red car (at rest for red)?

If you're asking about the two outside vertical red lines, then, yes, they are 12 feet apart, but you were not talking about those two lines, you were talking about the proper red length between A and C, which is 6 feet. Here's what you said:

the proper red length (12) between A and C; i.e. the line (not drawn in your IRF charts but essential in Loedel -and SR!) between A and C because that line is the collection of events the shorter train is made of. Same remark for proper green length between E and G (12).

And E-G is the proper length between green's fingertips, not the green train in the second diagram.

Correct. Sorry about that. My mistake.

And you made the same mistake regarding A-C, correct?

I thought I did what you wanted. Did you see the line segments A-D-C and E-H-G? Maybe you're looking at it on a small screen.

I saw them full scale, but they are not what I asked.
Once more: quote<<Draw on the diagram the light paths from the rear and front of the green rest train and see where they end at red's head. That's a complete different story, irrelevant for red's measurement of a shorter green train.>>

Now this one is my mistake. I didn't do what you asked but here it is now:

But I still don't understand why you want this drawing, please explain.

In fact you should draw a line between E-G en continue to the green worldlines of the front and rear of green car. The line is 'made of'/represents all the events that are simultaneous for green at one moment of time on green's wristwatch.
Similar reasoning for red. That red line is 'made of'/represents all the events that are simultanoeus for red.

The second diagram already has a grid line corresponding to simultaneous events that include events E and G and the first diagram has a grid line corresponding to simultaneous events that include A and C.

Dalespam...

I'll let him comment if he wants to.

 

[ghwellsjr]

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

I never heard of events belonging to just one object.

How did you determine the values of 12 and 6? Where did you get this ruler from that has those markings?

Where do you see on this diagram that the two observers are traveling at 0.866c relative to each other?

 

[TheBC]

O.K. guys, this is getting out of hand. It's really too ridiculous to waste more time on this.
I'll get back to this forum the day you know what events are, how loedel works, and what SR is about.
Untill then; good luck with your coordinate effects.

 

[ghwellsjr]

O.K. guys, this is getting out of hand. It's really too ridiculous to waste more time on this.
I'll get back to this forum the day you know what events are, how loedel works, and what SR is about.
Untill then; good luck with your coordinate effects.

How do you expect me to know how loedel works if you won't answer my simple questions:

How do you portray the relative speed of 0.866c between the two observers in your diagram?

How do you calibrate your ruler?

 

[Dale]

A Loedel diagram works the exact same way that any spacetime diagram works. All it is is a standard spacetime diagram from the "halfway" frame with the two moving frame's axes drawn and the "halfway" frame's axes suppressed. You are not missing anything, ghwellsjr.

You calibrate your ruler by the usual Lorentz factor in the "halfway" frame. You find the relative speed by looking at each moving frame's coordinates, although that is rather difficult to do. By events belonging to an object he just means that those events are on the world-tube of the respective object.

I prefer your clean diagrams. Less (clutter) is more (informative).

 

[ghwellsjr]

I wonder what people think of the following scenario (unfortunately not feasible, in practice):


Imagine two space beacons at mutual rest, separated by e.g. a million kilometers. A rocket passes them, turns, passes them again, turns, etc. On each passage the speed of the rocket relative to the beacons increases. The rocket can directly measure (theoretically) the relative speed of a beacon by measuring the time it takes to traverse the length of the rocket. The rocket can also measure the time it takes for both beacons to pass. [All acceleration occurs during the turnarounds, so no proper acceleration is measured in the rocket while the beacons are passing.]

On the first, slow, crossing the rocket measures D as the beacon separation by computing v (measured locally as described above) multiplied by the crossing time. However, following the identical procedure each time to measure v, and crossing time, D will be found to get smaller and smaller as v increases closer to c on each passing.

Note that since v is measured locally by the rocket on each passing, using its own clock, time dilation plays no role in this (at least for the rocket).

1) Do any of the participants believe that if the enormous engineering problems could be solved, that the observed result would be different from what is described above?

2) If not, is there any explanatory model other than distance contraction (at least for the rocket)?

All measurements are local measurements in a rocket inertial frame. We measure speed of a passing beacon, and time between one passing and then the other. One pair of local clocks, one ruler, all on/in rocket are all that are used.

I would like to draw some spacetime diagrams to depict what I think you are proposing. However, I prefer to work with feet rather than meters so that I can use the speed of light as 1 foot per nanosecond or 1 billion feet per second. I set the distance between the beacons in their mutual rest frame at 3 billion feet which is just a little shorter than a million kilometers. (I'm using the American definition of billion here, 10⁹.) I'm also using a very long rocket, 1 billion feet, just so that it will show up clearly on the diagrams but it won't make any difference to the principles illustrated.

I start with the mutual rest frame of the two beacons in green and red and the rocket with its front end in black and its rear end in blue approaching from the left at 0.6c. The dots on the rocket's worldlines mark off 1-second increments of Proper Time on the two clocks that you mentioned:

Now I transform to the rest frame of the rocket where we see that its length is 1 billion feet and its two clocks have been synchronized and correspond to the Coordinate Time:

Correct me if I'm wrong but I believe you described the rocket's measurement of the distance between the two beacons starting with it determining the speed of at least one of the beacons. It does this by noting its time on the black clock (0 secs) when the beacon passes it. Then it observes the time on the blue clock (1.667 secs) when the beacon reaches the rear of the rocket. Since its ruler (basically the rocket itself) sets the distance between these two measurements at 1 billion feet, it determines the speed of the beacon to be 1 billion feet divided by 1.667 seconds or 0.6 billion feet per second which is the correct answer of 0.6c.

Next the rocket measures the time that the second red beacon passes it (4 seconds) and determines that the distance between the two beacons is d=vt or 0.6 billion feet per second times 4 seconds which equals 2.4 billion feet, the correct length-contracted answer.

I want to emphasize the point that although we show these measurements being made in the rocket's rest frame, it doesn't matter which frame we use to describe the scenario. For example, you can go back to the first diagram, the mutual rest frame of the beacons and the exact same measurements and observations and determinations are made.

The particular scenario that I presented was in the middle of the iterative process that you described: in particular, the rocket has made many crossings, accelerating and reversing direction after each one so that each successive crossing is made at a higher speed. However, there are two problems with the scenario as described. The first is that the two clocks will not remain in sync after the rocket has accelerated and so they will have to be re-synced. The second is that there is no guarantee that the length of the rocket (or ruler) will remain the same Proper Length after it undergoes the acceleration. We can solve both of these problems by using the radar method to re-sync the remote clock and re-calibrate the length of the rocket. Here is a spacetime diagram to show how this is done using the same speeds and distances as the first set. You can assume that the clocks begin out of sync (as shown in the diagram) and the exact rocket length is unknown because this scenario is just one in a long line of iterations:

Some time after the turn-around acceleration when all the stresses have dampened out but before the rocket has reached the first beacon, the captain at the black front end of the rocket (at his time of -3 secs) sends a radar signal to the blue rear end of the rocket (shown as the bottom thin black line) which either passively reflects the signal back or actively regenerates a return signal (instantly) which the captain receives at his time of -1 secs (shown as the thin blue line). He then applies Einstein's synchronization convention (his second postulate) and assumes that the time it took for the radar signal to get to the rear of the rocket is equal to the time it took for the return to get back to him. He takes the half-way point of the interval (-2 secs) and assumes that the radar signal arrived at the rear at that time. But now he also knows that it will take another second for a message that he sends at his time of -1 secs to get to the rear of the rocket which means that his own clock will then be at 0 secs. So he tells the operator at the rear of the rocket (or has automatic equipment to do this) to set his clock to 0 secs when he receives the message.

Furthermore, since the roundtrip time for the radar signal to get to and from the rear of the rocket was 2 seconds, the captain assumes that the length of the rocket is one-half the distance that light travels during that interval or 1 light-second or 1 billion feet.

Now the captain can pick up his measurements as he did before. I go through this explanation because the captain will have to perform it again after each acceleration and change of direction before the next crossing.

Next I want to show how the same process works in the mutual rest frame of the beacons:

Note that the captain's assumption that the signal takes the same amount of time to get to the rear of the rocket as it does to return is not correct in this frame but it doesn't matter. And the determination of the length of the rocket is not correct. Neither is the calculation of the speed of the beacons or their distance apart. Everything's wrong except that this frame correctly shows exactly the same measurements and observations as was determined in the rocket's rest frame where everything was correct. This is to again emphasize the point that the frame that we are depicting the scenario in has no bearing on the measurements, observations, assumptions and determinations for the captain.

But now I want to show that there is an even simpler way for the captain to make his determination of the distance between the beacons and yet it involves the same process of radar signals but doesn't require a ruler or a second clock or the need to synchronize or re-calibrate them.

In this process, the captain makes successive radar measurements of the distance to one of the beacons and from this he can determine its speed. He can do this before the beacon gets close to him or after it passes him. I will take advantage of one of those measurements when the beacon passes the captain and the distance is zero. Some arbitrary time later, I use one second simply because it is convenient, he sends out a radar signal which returns to him at his time of 4 seconds. From this he determines that at his time of 2.5 seconds (half-way between sending and receiving) the beacon was 1.5 light-seconds or 1.5 billion feet away. From these he determines its speed to be 1.5/2.5 or 0.6c, just like before. And he determines the distance between the beacons just like before as 0.6 times 4 or 2.4 billion feet:

Finally, I show this last process in the mutual rest frame of the beacons:

Again, all measurements are the same.

 

[ghwellsjr]

Now as if things didn't get simple enough, we can make them even simpler. It is not necessary for the captain to first determine the speed of the beacons in order to calculate their separation. He can do it directly with radar signals. Of course, he can't know ahead of time when to send out the radar signals so we imagine that he is doing it continuously but I'm only going to show the important ones. He would send out one set of signals to the green beacon and a second set to the red beacon and by matching the times determined by the reflections, he can determine the distance between the beacons.

To start with, though, I'm going to take advantage of the fact that he is colocated with one of the beacons at a particular time and so he only has to measure the distance to the other beacon. Here is the diagram for that situation:

A few seconds after he has passed the green beacon, he looks at his log of sent/received radar times for the red beacon and finds one that determines a measurement taken at the same time he was colocated with the green beacon, his time of zero seconds and that is the one that I show in the above diagram. He notes that he sent that radar signal at his time of -2.4 secs and received the return signal at 2.4 secs which allows him to determine that the red beacon was 2.4 light-seconds or 2.4 billion feet away.

Here is how it looks in the rest frame of the beacons:

If the captain is keeping track of the speed versus Length Contraction for the different iterations, he can calculate the speed as 2.4 light-seconds divided by 4 seconds or 0.6c.

He looks in his log and finds another set corresponding to this diagram:

The two radar signals above were sent in opposite directions at his time of 0.8 secs and received at his time of 3.2 secs. Since these obviously calculate to the same time, the distance in each direction is simply (3.2-0.8)/2=2.4/2=1.2 billion feet or a total of 2.4 billion feet.

Here's how this one looks in the beacons' rest frame:

The captain continues to look in his log and finds one corresponding to this diagram:

In this one, the signals to the two beacons were sent in the same direction (behind him). The one to the green beacon was sent at 2 secs and the return received at 8 seconds. One half of the difference is 3 seconds corresponding to a distance of 3 light-seconds or 3 billion feet and the time is the average or 5 seconds. The signal to the red beacon was sent at 4.4 secs and its return arrived at 5.6 secs. One half of the difference is 0.6 seconds corresponding to a distance of 0.6 billion feet at a time of 5 seconds. The difference between the two distance measurements is 3-0.6 or 2.4 billion feet.

Finally, the same scenario in the rest frame of the beacons:

 

[PAllen]

I would like to draw some spacetime diagrams to depict what I think you are proposing. However, I prefer to work with feet rather than meters so that I can use the speed of light as 1 foot per nanosecond or 1 billion feet per second. I set the distance between the beacons in their mutual rest frame at 3 billion feet which is just a little shorter than a million kilometers. (I'm using the American definition of billion here, 10⁹.) I'm also using a very long rocket, 1 billion feet, just so that it will show up clearly on the diagrams but it won't make any difference to the principles illustrated.

...

Thanks a lot for these and the following series of illustrations. Indeed, you have understood my scenario perfectly.

However, I want to discuss two points you raise and also motivate the seeming complexity of what I proposed.

My first goal was to verify whether or not universal_101 (in obsessing over the idea that length contraction has not been 'directly' observed) believed that an attempt to do so would come out differently than SR predicts. For this purpose, I wanted an in principle experiment which would be hard to understand as anything other than length contraction and also one that used only procedures valid both for Newtonian mechanics and SR. It would thus, if achieved, select SR, via observed length contraction, using no assumptions that distinguish SR from Newtonian mechanics (e.g. invariant two way lightspeed, which is false both in Newtonian corpuscular theory or pre-SR aether theory).

As you note, I glossed over the issues of synchronizing the clocks in front and back of the rocket, and also the constancy of the length of the rocket. I will now un-gloss over those issues, showing how they could be addressed exactly, in principle, in the meta-theory encompassing Newtonian physics and SR. The key features of the meta-theory are the POR and homogeneity and isotropy.

First, as to ship length, all we need assume is that prior to constructing the rocket we have found ideally rigid materials, with rigidity so defined as to be perfectly consistent with SR as well as Newtonian physics. A simple approach is that the material however, stressed, when unstressed and allowed time for relaxation, exactly retains all of its dimensions (as long as it doesn't break). There is no classical theoretical lower limit to coefficient of thermal expansion, so we can propose a value of zero for our ideal material. This definition of rigidity is perfectly consistent with both SR and Newtonian physics and removes the need to re-measure the rocked after turnarounds - we just need to allow for time for relaxation (and SR does provide a precise lower bound on the minimum time for this).

Second, as to the clocks, we need a procedure to ensure they remain in synch that is exactly valid both for Newtonian physics and SR. This means we can not use either slow clock transport (exactly valid in SR only in a theoretical limit of infinite time), nor light signals (because we don't want to assume SR). The key hint is isotropy and homogeneity. We move two perfect clocks to the center of the rocket and synchronize them. When we want to make an inertial measurement with the clocks separated, we move them with identical motion profiles to opposite ends of the rocket. As this is done while the rocket is inertial, these two clocks remain exactly synchronized with respect to each other, in both SR and Newtonian physics (in SR, they would no longer be in synch with a clock that remained at the center, but we don't care about this). This procedure is relying on homogeneity and isotropy guaranteeing that the result is the same as long as the motions are symmetric. Then, before any acceleration of the rocket, we move the clocks back to the center, again with exactly symmetric motion.

 

[nitsuj]

My first goal was to verify whether or not universal_101 (in obsessing over the idea that length contraction has not been 'directly' observed) believed that an attempt to do so would come out differently than SR predicts. For this purpose, I wanted an in principle experiment which would be hard to understand as anything other than length contraction and also one that used only procedures valid both for Newtonian mechanics and SR.

Has time dilation from relative velocity been "directly" observed in a more "direct" way then length contraction? I don't think so.

Differential aging from relative motion is as much a result of time dilation as it is length contraction, specifically the invariance of c.

imo this seems to be more about hammering out a definition of "directly" observed, and in the context of variant measurements

 

[PAllen]

Has time dilation from relative velocity been "directly" observed in a more "direct" way then length contraction? I don't think so.

Differential aging from relative motion is as much a result of time dilation as it is length contraction, specifically the invariance of c.

imo this seems to be more about hammering out a definition of "directly" observed, and in the context of variant measurements

Muon's reaching the ground is accepted (even by skeptics in this thread) as a direct measure of time dilation in the Earth frame (not twin differential aging). In the muon frame it would be an observation of length contraction, but 'we' are not in the muon frame. In my scenario, my rocket frames (for each inertial velocity) create a family of 'muon frames' in relation to the beacons, with a direct way of measuring a long length - and finding it getting shorter and shorter.

 

[nitsuj]

Muon's reaching the ground is accepted (even by skeptics in this thread) as a direct measure of time dilation in the Earth frame (not twin differential aging).

That's what I'm finding so bizarre is that is accepted as a "direct" measure of time dilation, but not length contraction, surely those "skeptics" agree the muons measure proper time. Also, I'd consider the "landing" of the muon the comparative of proper times and noting differential aging. However I don't see any "direct" measure of time dilation.

In the muon frame it would be an observation of length contraction, but 'we' are not in the muon frame. In my scenario, my rocket frames (for each inertial velocity) create a family of 'muon frames' in relation to the beacons, with a direct way of measuring a long length - and finding it getting shorter and shorter.

A neat way to illustrate it for sure!

 

[PAllen]

That's what I'm finding so bizarre is that is accepted as a "direct" measure of time dilation, but not length contraction, surely those "skeptics" agree the muons measure proper time. Also, I'd consider the "landing" of the muon the comparative of proper times and noting differential aging. However I don't see any "direct" measure of time dilation.

Differential aging refers to two clocks that start and end coincident. The result is that the ensuing discrepancy in their measured times is not only invariant, but that the explanation is time dilation in alll reference frames. Sometimes forgotten is that where the time difference emerges along the world lines is frame dependent, so the idea of a frame dependent explanation is in common with the muon case (except that it always involves time dilation).

The muon case is definitely not a case of differential aging. There are no two clocks that separate and come together. In one frame you have pure time dilation (not differential aging). In another frame you have pure length contraction - no time dilation at all involved in the explanation.

 

[nitsuj]

The muon case is definitely not a case of differential aging. There are no two clocks that separate and come together. In one frame you have pure time dilation (not differential aging). In another frame you have pure length contraction - no time dilation at all involved in the explanation.

Ah i See

 

[bobc2]

Excellent 4-D Pictures

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

TheBC, I've appreciated your many efforts at explaining Special Relativity with your Loedel space-time diagrams. Good work! It saddens me to see the response you get on the forum. Particularly when your sketches are passed off as meaningless, since they are merely coordinate representations -- as though coordinate representations have no relevance to reality. That's like telling your physics instructor in a General Physics class that his picture of the trajectory of a cannon ball has no relevance to reality because it is merely a coordinate representation. And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target. You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

 

[Mentz114]

And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target. You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

I think most posters here understand what the Loedel diagram means. But it picks two inertial frames and shows only those. The regular Minkowski diagram can be transformed to show the POV of any set of inertial frames.

I suggest that insisting that the Loedel diagram is better in some way is just prejudice on your part. Insulting people who don't agree with you is just offensive and unnecessary.

 

[bobc2]

TheBC Loedel Diagrams

I think most posters here understand what the Loedel diagram means. But it picks two inertial frames and shows only those. The regular Minkowski diagram can be transformed to show the POV of any set of inertial frames.

I hope you are not implying that the choice of which pair of observers is limited. Of course that is not the case. Any two observers in motion with constant velocity with respect to each other may be selected for a Loedel-Minkowski diagram. And there has been no claim that the Loedel-Minkowski diagram is always the preferred method of presenting the concept. The standard Minkowski diagram together with the Loedel-Minkowski representation is usually quite useful.

The Loedel-Minkowski picture is particularly applicable to the subject of this thread. My comments were not meant as an insult to anyone but rather as a compliment and encouragement to TheBC for his excellent presentations and persistence under hostile posts.

 

[ghwellsjr]

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

TheBC, I've appreciated your many efforts at explaining Special Relativity with your Loedel space-time diagrams. Good work! It saddens me to see the response you get on the forum. Particularly when your sketches are passed off as meaningless, since they are merely coordinate representations -- as though coordinate representations have no relevance to reality. That's like telling your physics instructor in a General Physics class that his picture of the trajectory of a cannon ball has no relevance to reality because it is merely a coordinate representation. And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target.

I didn't think TheBC agreed that Length Contraction was simply a coordinate effect:

O.K. guys, this is getting out of hand. It's really too ridiculous to waste more time on this.
I'll get back to this forum the day you know what events are, how loedel works, and what SR is about.
Untill then; good luck with your coordinate effects.

You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

Since you have been a teacher of Loedel diagrams then maybe you can answer my simple questions to TheBC from post #148:

How did you determine the values of 12 and 6? Where did you get this ruler from that has those markings?

Where do you see on this diagram that the two observers are traveling at 0.866c relative to each other?

 

[Mentz114]

My comments were not meant as an insult to anyone but rather as a compliment and encouragement to TheBC for his excellent presentations and persistence under hostile posts.

Sure. I suppose that if 'complicated' is taken as meaning 'clutterful' then it is too complicated. But never in the other possible sense of complicated.

 

[jartsa]

How so? I don't get what you think the problem is.

Regarding reciprocal, in the Earth's frame the muon is contracted, in the muon's frame the Earth is contracted. Again, no problem. Just apply the Lorentz transform from one frame to get the other. No problem.

A fast muon thinks the distance to Earth is contracted and short.

Earth thinks the distance to the same muon is contracted and long.

Well, Earth should think that way IMHO. It should think: "Just by going into a different frame I can make the distance longer, the uncontracted distance is the longest of the distances in different frames."


Is it possible for the earh to make the distance longer?
Well, it's possible for the muon, so reciprocally it should be possible for the earth.

 

[Dale]

Earth thinks the distance to the same muon is contracted and long.

The distance to the muon is changing over time, so the length contraction formula doesn't even apply. You cannot use a formula in a circumstance which violates one of the assumptions used in the derivation of the formula. The distance between the Earth and the muon requires the full Lorentz transform, not just the simplified length contraction formula.

The distance between the top of the atmosphere (muon source) and the bottom of the atmosphere (muon detector) is not changing over time, so the length contraction formula applies. That distance is uncontracted in the Earth's frame and contracted in the muons frame.

 

[nitsuj]

Differential aging refers to two clocks that start and end coincident.

I've searched a fair bit for any definition for Differential aging and haven't found anything. Where did yours come from? Can you direct me to a source?

Also it reads as though muon decay is very consistent...like a clock, and is the point to them being reliable for such experiments. If muons decay at the same rate, the lifetime taken in a lab compared to the life time of those atmosphere ones seems to circumnavigate that before 'n after clock comparison requirement for differential aging that you mentioned.

So I guess I don't see your perspective, less the "we are not in the muons frame see we don't measure length contraction." Though the muon it self is length contracted in the "at home" frame so with magical idealized measurements I suppose it could be "directly" measured.

Here is wikis definition for time dilation;
"In the theory of relativity, time dilation is an actual difference of elapsed time between two events as measured by observers..."

What is the elapsed time the muon measures? rhetorical.

 

[PAllen]

I've searched a fair bit for any definition for Differential aging and haven't found anything. Where did yours come from? Can you direct me to a source?

Also it reads as though muon decay is very consistent...like a clock, and is the point to them being reliable for such experiments. If muons decay at the same rate, the lifetime taken in a lab compared to the life time of those atmosphere ones seems to circumnavigate that before 'n after clock comparison requirement for differential aging that you mentioned.

So I guess I don't see your perspective, less the "we are not in the muons frame see we don't measure length contraction." Though the muon it self is length contracted in the "at home" frame so with magical idealized measurements I suppose it could be "directly" measured.

Here is wikis definition for time dilation;
"In the theory of relativity, time dilation is an actual difference of elapsed time between two events as measured by observers..."

What is the elapsed time the muon measures? rhetorical.

Differential aging is the more technical term for twin paradox scenario. The fundamental feature is that both twins (clocks) agree which one elapsed more time. The defining feature is two clocks starting and ending together, thus two space time paths between one pair of events.

Time dilation is frame or coordinate dependent and, in SR, is symmetric. The muon considers Earth clocks to be slow; the Earth considers the muon clock (decay rate to be slow). Time dilation is defined as the ratio between the rate on some clock moving in some coordinate system and the time measured in that coordinate system. It can be defined for one world line expressed in some coordinates. Indeed, there is only one world line of interest between the muon creation and detection - the muon world line. There is no other clock that follows a different path between the creation and detection event.

This single muon world line elapses much less than two microseconds proper time, in all frames. In the muon frame, there is not time dilation at all - the ratio of proper time to coordinate time is 1. Instead, the explanation of why it reaches the ground is that the ground is very close at the time (per the muon) that the muon is created. Also, in this frame, the ratio of Earth clock rate to muon coordinate time is <<1, but this has no bearing on why the ground reaches the muon.

For earth, the ground and muon are far apart at the time (per earth) of muon creation. The muon reaches the ground by virtue of time dilation: the ratio of proper time on the muon world line to Earth coordinate time is <<1. Also, if two muons created in succession are 1 meter apart as they measure it (assuming they are co-moving, thus mutually stationary), they are <<1 meter apart per Earth coordinates - but this has no relevance to why they reach the ground, using Earth coordinates.

 

[ghwellsjr]

Time dilation is defined as the ratio between the rate on some clock moving in some coordinate system and the time measured in that coordinate system.

Although we often refer to the rate of a clock, it's actually the period of a time interval on a clock that we are concerned with since Time Dilation means something is stretched out--gotten bigger (the opposite of Length Contraction). Seconds last longer on a moving clock compared to the seconds of the coordinate system. So the precise definition of Time Dilation is the ratio of the Coordinate Time to the Proper Time of a clock moving according to the coordinate frame. Thus the Time Dilation factor is always a number greater than 1. It's equal to the Lorentz Factor known as gamma.

 

[ghwellsjr]

A fast muon thinks the distance to Earth is contracted and short.

Earth thinks the distance to the same muon is contracted and long.

Well, Earth should think that way IMHO. It should think: "Just by going into a different frame I can make the distance longer, the uncontracted distance is the longest of the distances in different frames."


Is it possible for the earh to make the distance longer?
Well, it's possible for the muon, so reciprocally it should be possible for the earth.

You can only appeal to reciprocity when the scenario is reciprocal (and symmetrical). We can change the scenario to one that is reciprocal and then we can apply Length Contraction equally.

So let's consider a spaceship that is 1000 feet long approaching the Earth at a speed of -99%c and we'll look at what happens as it reaches a point in the sky that is 1000 feet above the surface of the earth.

I'm going to draw some spacetime diagrams that are a little unusual in the sense that they have distance along the vertical axis and time along the horizontal axis. I think this will make it clearer in thinking about the spaceship coming straight down towards the Earth (or the Earth coming up straight towards the spaceship).

The surface of the Earth is shown as a green line with the point in the sky at 1000 feet in blue. The front end of the spaceship is shown as a black line and the rear in red. To begin with, I put the origin of the diagram at the point of contact between the black front of the spaceship and the blue point in the sky. That is why the surface of the Earth is at -1000 feet in the first diagram. The dots represent 1-microsecond intervals of time covering a range of just 2 microseconds. The speed of light is 1000 feet per microsecond.

Here's the first diagram showing the rest frame of the earth/sky:

Now I transform the coordinates of the first diagram to a frame moving at -99%c which is the rest frame of the spaceship:

If you compare these two diagrams, you will see that they are exactly reciprocal. The Lorentz Factor at 99%c is just over 7 so the time for the moving object is dilated meaning that 2 usecs of its Proper Time takes 14 usecs of Coordinate Time and the 1000-foot distance for the "objects" is Length Contracted from 1000 feet to 141 feet. Note also that because of the Relativity of Simultaneity, the Proper Time at one end of the object is offset from the other end of the object.

But to get closer to the situation for a muon, we need to use a shorter length for the spaceship. A muon is actually a very small fraction of a foot but I'm just going to shorten the length from 1000 feet to 100 feet so that you can see the trend:

Note now that the offset between the front and rear of the spaceship is one seventh of what it used to be and the distance between the black and red lines is not even visible on the diagram. I think you can see that if we went a million times smaller, there would be no practical difference between the black and the red lines. So this represents the first point of departure from a reciprocal scenario to one that is not reciprocal.

Next, we want to make several changes in the relationship between the surface of the Earth and the point in the sky. First, we want to make the point of contact (the origin) be the surface of the Earth and not someplace up in the sky. In fact we want to consider the point in the sky as being analogous to the creation of the muon and so it must occur much earlier so we need to extend the timeline of the earth/sky to 15 microseconds instead of only 2 microseconds. Here's the spacetime diagram for the final scenario:

Note that in the above diagram, the time for the Earth is the same as the Coordinate Time and the time when the spaceship arrives at the 14000-foot altitude above Earth is just over 14 microseconds before the time of impact with the surface of the earth. Note also that time for the spaceship is dilated so that 2 seconds on its clock is stretched out to just over 14 microseconds of Coordinate Time during its trip. Finally, note that the length of the spaceship has been contracted so that instead of 100 feet (which would be noticeable on the diagram) it is only 14 feet (which is not noticeable).

Now we want to see what this scenario looks like when we transform to the rest frame of the spaceship. I have to change the scale of the coordinates so that it will fit on the page:

Unfortunately, we lose all the important details so I'll zoom back into the same scale I had before and focus on the activity of the spaceship:

Now we can see that the time for the Earth and sky is dilated so that each microsecond of their Proper Time is stretched out to just over 7 microseconds of Coordinate Time. We can also see the Proper Length of the spaceship at 100 feet but the distance between the sky and the Earth is contracted from 14,000 feet to about 2000 feet.

So as you can see, Time Dilation and Length Contraction still apply to both the earth/sky frame and the spaceship frame, it's just that the Earth doesn't care about how the spaceship is Length Contracted (and especially for a muon that is billions of times smaller than a spaceship), the Earth only cares about the Time Dilation of the spaceship (or muon) so that it can survive a 14,000 foot trip at 99%c in only 2 microseconds of its time. Without Time Dilation, it would not even be able to get down to the 12,000-foot altitude.

And the spaceship (or muon) doesn't care about how time for the earth/sky is dilated (even though it is), it only cares about the Length Contraction of the distance between the sky at 14,000 feet and the surface of the Earth (at zero feet) which is contracted to about 2000 feet. So instead of the Earth starting out at 14,000 feet below it, it starts out at only 2000 feet below it and coming up at 99%c so that it only takes 2 microseconds of its own time for the Earth to reach the spaceship (or muon).

So the bottom line is that since the final scenario is not symmetrical and reciprocal, the details of how we apply both Time Dilation and Length Contraction are not the same in both frames like they were in the first symmetrical scenario.

Does that make it all perfectly clear? Any Questions?

 

[ghwellsjr]

For those that would like to see the spacetime diagrams in the previous post in the normal format, here are thumbnails for them:

 

[PAllen]

Although we often refer to the rate of a clock, it's actually the period of a time interval on a clock that we are concerned with since Time Dilation means something is stretched out--gotten bigger (the opposite of Length Contraction). Seconds last longer on a moving clock compared to the seconds of the coordinate system. So the precise definition of Time Dilation is the ratio of the Coordinate Time to the Proper Time of a clock moving according to the coordinate frame. Thus the Time Dilation factor is always a number greater than 1. It's equal to the Lorentz Factor known as gamma.

I agree this is the standard definition for time dilation factor. However, I did not actually use that term. I spoke of rate of time on clock to coordinate time being << 1, which is correct, and is time dilation.

 

[ghwellsjr]

I agree this is the standard definition for time dilation factor. However, I did not actually use that term. I spoke of rate of time on clock to coordinate time being << 1, which is correct, and is time dilation.

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

 

[DrGreg]

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

"Time" and "rate" are reciprocals of each other, so "rate contraction" means the same as "time dilation". But no-one ever uses the phrase "rate contraction".

 

[PAllen]

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

To me, time dilation is the name of the phenomenon: a particular clock runs at a different rate than reference clocks; for inertial frames in SR, this is more specifically a moving clock runs slow compared to stationary reference clocks. You can mathematically describe this phenomenon in multiple ways. The most common in SR is a a factor saying how many times slower the observed clock is = seconds of coordinate time per second of clock time. However, I was interested in comparing the rates the other way: seconds elapsed on observed clock compared to seconds measured by reference clocks. I was careful to define my terms, so I don't see what the problem is.

[addendum: which is right, "price to earnings ratio" or "earnings to price ratio"? The former is more common, both are used, and both describe the same underlying thing.]