Plotting the Poynting vector of a radiating electric dipole [matlab]

[PhDeezNutz]

Please zoom in (I apologize for the scale, I'm working on it) to see that the wave is propagating outwards but the level surfaces (or rather cross sections of level surfaces) appear to be pointing inwards instead of outwards.

I'm off by a phase factor of $i$ somewhere in my purely spatial dependencies because when I multiply by $e^{i \omega t}$ instead of $e^{- i omega t}$ I get the wave propagating outwards. Which runs completely opposite of what is supposed to happen.

This gif/program needs a lot of work.

Summary

1) Off by a phase factor somewhere in my 30 pages of derivations

2) Level surfaces are pointing in instead of out

maybe the 2 problems are related to each other.

 

[PhDeezNutz]

Has 6 loves instead of 4 it seems. awful.

 

[TSny]

Would it be alright If I continued the quest to create a quadrupole animation in this thread for the time being?

That's ok with me. But, one of the advisors or mentors might shut this thread if he/she feels that it's becoming too lengthy.

As a note: I didn't use the fields that Jackson used but rather my own expressions, but they do corroborate Jackson to first order. Jackson uses the approximation that $\nabla \times \approx \hat{n} \times$ in the far field which I think is ridiculous.

$\nabla \times \approx ik\hat{n} \times$ is a good approximation in the radiation zone when applied to the complex valued expression for vector potential $\vec A$.

Are you trying to get expressions that are valid in the "intermediate zone" as well as in the radiation zone. If so, I imagine the expressions will be pretty lengthy.

What are you taking to be the charge distribution that defines the quadrupole? That is, what are you taking for the components of the quadrupole moment tensor, $Q_{ij}$?

 

[PhDeezNutz]

That's ok with me. But, one of the advisors or mentors might shut this thread if he/she feels that it's becoming too lengthy.
$\nabla \times \approx ik\hat{n} \times$ is a good approximation in the radiation zone when applied to the complex valued expression for vector potential $\vec A$.

Are you trying to get expressions that are valid in the "intermediate zone" as well as in the radiation zone. If so, I imagine the expressions will be pretty lengthy.

What are you taking to be the charge distribution that defines the quadrupole? That is, what are you taking for the components of the quadrupole moment tensor, $Q_{ij}$?

Alright I'll start a new one as soon as I get enough material to do so. I'm trying to get one in the intermediate and near zone as well. And I realized my attempt to do so fails badly, I went back and looked over my work and conflated spherical basis with cartesian.

Allow me to explain:

I Believe these are correct.

I also believe the following is true

$\vec{E} = \frac{i}{k\sqrt{\mu \epsilon}} \nabla \times \vec{B}$ is true assuming harmonic fields.
Now computing the latter expression for the former is where I'm having lots of difficulty. I incorrectly assumed in my derivation that $Q\vec{r}$ was a spherical construction as opposed to a cartesian construction. So I must convert...a lot of work ahead of me.

I assumed there charges

$+q$ @ $(d,0,0)$
$-q$ @ $(0,0,d)$
$+q$ @ $(-d,0,0)$
$-q$ @ $(0,0,-d)$

I think that gives us the only nonzero quadrupole moments

$Q_{11} = 6qd^2$

$Q_{22} = -6qd^2$

using the traceless quadrupole definition.

But truth be told I messed up long before I put the Quadrupole moments into my program.

 

[TSny]

I Believe these are correct.

View attachment 257575

I'm not familiar with these expressions. But I have no reason to doubt them.

I also believe the following is true

$\vec{E} = \frac{i}{k\sqrt{\mu \epsilon}} \nabla \times \vec{B}$ is true assuming harmonic fields.

I think this is correct.

I assumed there charges

$+q$ @ $(d,0,0)$
$-q$ @ $(0,0,d)$
$+q$ @ $(-d,0,0)$
$-q$ @ $(0,0,-d)$

OK. So, you have four charges on the corners of a square with alternating signs of the charges as you go around the perimeter of the square. You placed the charges in the x-z plane.

I think that gives us the only nonzero quadrupole moments

$Q_{11} = 6qd^2$

$Q_{22} = -6qd^2$

using the traceless quadrupole definition.

With the charges in the x-z plane, wouldn't $Q_{22} = 0$ and $Q_{33} = -6qd^2$?

 

[PhDeezNutz]

I'm not familiar with these expressions. But I have no reason to doubt them.I think this is correct.

OK. So, you have four charges on the corners of a square with alternating signs of the charges as you go around the perimeter of the square. You placed the charges in the x-z plane.

With the charges in the x-z plane, wouldn't $Q_{22} = 0$ and $Q_{33} = -6qd^2$?

I meant to put the negative charges on the y-axis. My bad for the typo.

Anyway I used my expression for$\vec{B}$, used the curl function in matlab, multiplied by the appropriate constant, took the cross product, plotted the vector field and got this

I'll keep working on it. This is not exactly what I want but it has enough of what I want to make me think that I made a small mistake somewhere.

 

[PhDeezNutz]

I'm going to test Jackson's formulas in MATLAB before I try implementing my own just to compare. Progress I think.

Had to project the vector field radially to get rid of the vectors "in between the lobes" and then make isosurfaces.

Edit: nvm I used the wrong power of $r$ in the denominator.

 

[PhDeezNutz]

Using my own formulas I'm getting something peculiar. My intent was to plot level surfaces of the Poynting vector for the radiating electric quadrupole at time $t=0$. It seems like I got an inverted level surface of an octupole pattern.

 

[PhDeezNutz]

I feel like this is progress.

I instead plotting Poynting vector magnitude level surfaces I plotted level surfaces of the power radiated per unit solid angle.

$\frac{dP}{d \Omega} = \frac{1}{2} Re\left( r^2 \hat{n} \cdot \vec{E} \times {H^*}\right)$

Edit: I used my own formula for the vector potential on this one and let MATLAB compute $\vec{H}$ and $\vec{E}$

 

[TSny]

That looks like it could be it!

 

[PhDeezNutz]

That looks like it could be it!

Thank you very much for your words of encouragement! They mean a great deal to me!

 

[TSny]

I tried cranking out expressions for the E and B fields. Pretty messy! I doubt if I got it all correct. If you want to compare, here are some contour plots of |S| for the xy plane, the xz plane, and a vertical plane that makes a 45^o angle with the x and y axes.

Here's a 3D contour plot for one value of |S|. The figure on the right is a closer look at the center region.

 

[PhDeezNutz]

Weird, I only get what you get when I project the vector field radially. Making the vectors in between the lobes essentially disappear.

But I'm probably wrong.

Edit: I'm having considerable trouble animating.

 

[PhDeezNutz]

Ever been so wrong that you were close to being right? That's how I feel right now.

My goodness gracious the quadrupole is more complicated than the dipole.

 

[TSny]

Looks like your last plot is for a region that is quite a bit less than a wavelength from the origin. The fields vary rapidly with position in this region. The "horns" along the coordinate axes correspond to the holes poking through your surface in post #79. I also get the horns as shown below. This shows a contour sheet of one particular value of $|\vec {S}|$. The region plotted is within $\lambda/5$ of the origin. $\vec S$ is zero for points on the coordinate axes.

 

[PhDeezNutz]

Looks like your last plot is for a region that is quite a bit less than a wavelength from the origin. The fields vary rapidly with position in this region. The "horns" along the coordinate axes correspond to the holes poking through your surface in post #79. I also get the horns as shown below. This shows a contour sheet of one particular value of $|\vec {S}|$. The region plotted is within $\lambda/5$ of the origin. $\vec S$ is zero for points on the coordinate axes.

View attachment 257724

I basically lost a bunch of what I did because I edited it without keeping record of what I did. This is what I've gotten back to. I'm going to try increasing $k = \frac{2 \pi}{ \lambda}$ in my program to get a shorter wavelength. ( I think that statement makes sense...my brain is fried)

Edit: and I get this

 

[PhDeezNutz]

If only I could get the purple surfaces to close. It conceal the rest of the level surfaces but it would get us the characteristic shape we want.

 

[PhDeezNutz]

Top view, I feel like those level surfaces should be pointing outwards.

 

[PhDeezNutz]

Part of me thinks that it's MATLAB connecting level surfaces that shouldn't really be connected.

 

[TSny]

If only I could get the purple surfaces to close. It conceal the rest of the level surfaces but it would get us the characteristic shape we want.

They purple surfaces might close if you plot out to a greater distance. To get the purple surface to close so that you see all of the "central blob", you need to plot out to a distance of approximately one wavelength.

I notice that you have a factor of $10^{11}$ for your tick marks on the axes. I find it much more convenient to choose the unit of distance to equal one wavelength. By letting $k = 2 \pi$ and $\omega = 2\pi$, the unit of length is one wavelength and the unit of time is one period of oscillation of the source. (In some of my earlier plots, such as in post #82, I let $k = 1$ which made $\lambda$ equal about 6.3 units of distance.)

 

[PhDeezNutz]

Did I inadvertently solve the octupole while trying to solve the quadrupole? I mean what is going on here.

 

[PhDeezNutz]

@TSny I may be terribly misguided but this is what I'm thinking. If you look on page 416 (Figure 9.2) of Jackson he talks about a system that is a little bit different than the one we're dealing with but the impression I get is that each vertical plane has a quadrupole (4 lobe pattern)...my picture has that feature so that is reassuring.

Granted Jackson's radiation pattern comes from the time averaged poynting vector radial flux...but I think the magnitude of $\vec{S}$ is closely connected to that...in a way I can't quite articulate.

 

[TSny]

@TSny I may be terribly misguided but this is what I'm thinking. If you look on page 416 (Figure 9.2) of Jackson he talks about a system that is a little bit different than the one we're dealing with but the impression I get is that each vertical plane has a quadrupole (4 lobe pattern)...

Jackson is assuming a charge distribution with cylindrical symmetry, such as a spheroid (ellipsoid of revolution). At the beginning of the paragraph containing equation (9.50) he assumes "an oscillating spheroidal distribution of charge". Figure 9.2 refers to this case.

 

[PhDeezNutz]

Jackson is assuming a charge distribution with cylindrical symmetry, such as a spheroid (ellipsoid of revolution). At the beginning of the paragraph containing equation (9.50) he assumes "an oscillating spheroidal distribution of charge". Figure 9.2 refers to this case.

I’m having trouble imagining what that means. Would that mean

$\rho (\vec{r}’) = \frac{3Q}{4 \pi R^3} e^{-i \omega t}$

It seems not much different than a point charge and I was under the impression that point charges don’t radiate unless accelerated.

 

[PhDeezNutz]

I feel like I'm getting the exact opposite of what I'm trying to get. In my opinion the level surfaces should connect close to the origin for a specified level. Instead they are connecting near the outside.

 

[PhDeezNutz]

Finally got it. Was missing a factor of $\frac{1}{r^3}$ in my vector potential for the oscillating quadrupole.

 

[TSny]

Yes, your last plot looks good to me.

I’m having trouble imagining what that means. Would that mean

$\rho (\vec{r}’) = \frac{3Q}{4 \pi R^3} e^{-i \omega t}$

It seems not much different than a point charge and I was under the impression that point charges don’t radiate unless accelerated.

A "spheroid" is an ellipsoid of revolution. See here. As Jackson mentions, the nonzero components of the quadrupole moment tensor are the diagonal elements. These satisfy $Q_{11} = Q_{22}= -\frac{1}{2}Q_{33}$. We imagine that somehow these components vary harmonically in time.

 

[PhDeezNutz]

I am very happy with this, got to change the viewing angle to catch the near field behavior but all in all I'm very happy.

I think this is the first gif of its kind. I've seen many quadrupole animations online but they are all confined to a plane. That could be because creating a 3D version is a trivial extension...but I'm proud of it.

 

[TSny]

Yes, that looks very nice. It would be interesting to see some of the near field behavior. Good work!

 

[PhDeezNutz]

Yes, that looks very nice. It would be interesting to see some of the near field behavior. Good work!

I tried changing the viewing angle but it didn’t show much. It showed something but not as much as I would like. I think the best approach will be to take slices.

I’ll have it by tonight hopefully. Count on it!

 

[PhDeezNutz]

@TSny do we dare tackle the octupole next? (I should probably get back to all my class work that I've been neglecting but the idea of tackling the octupole is very enticing)

I am very happy right now.

 

[PhDeezNutz]

@TSny I’ve thanked you many times in this thread but I really can’t thank you enough. You truly went out of your way to help me, maybe one day I’ll be able to pay it forward. I look forward to that day.

 

[PhDeezNutz]

@TSny may I ask what the definition of the (primitive, non-traceless) Magnetic Quadrupole moment is?

Is it

$M_{ij} = \sum I_{\ell} (a_i)(a_j)$

Where $a_i$ is the #ith#-component of the area vector.

 

[TSny]

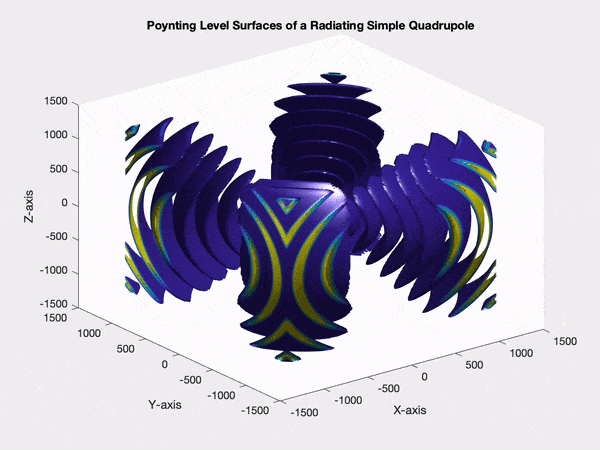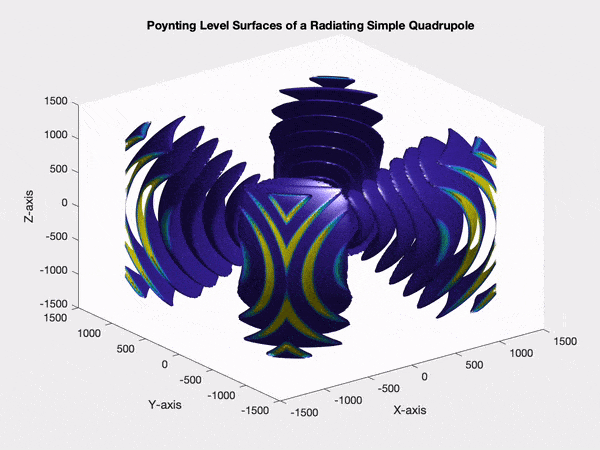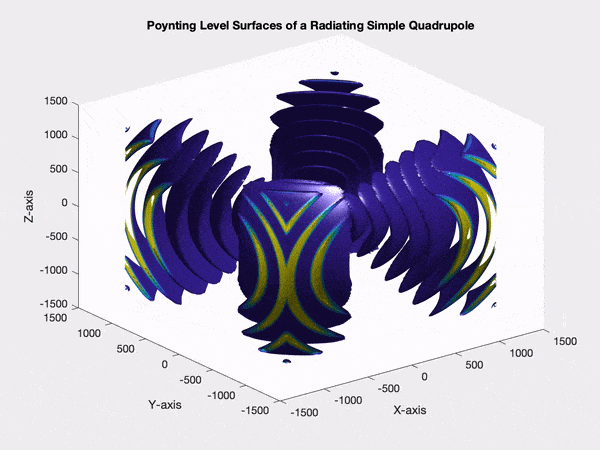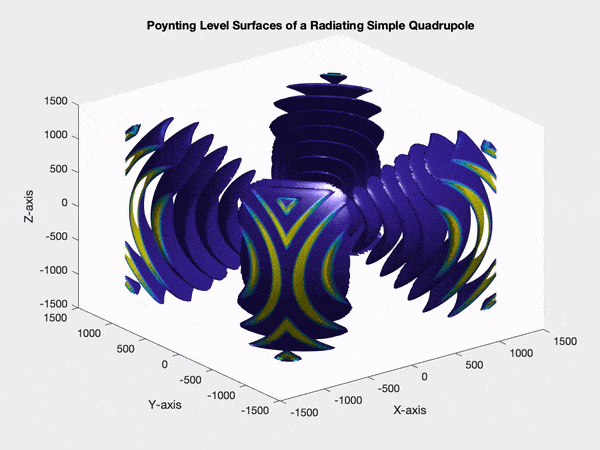
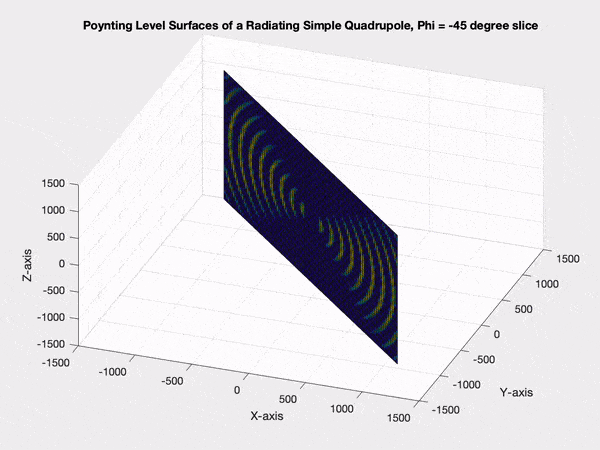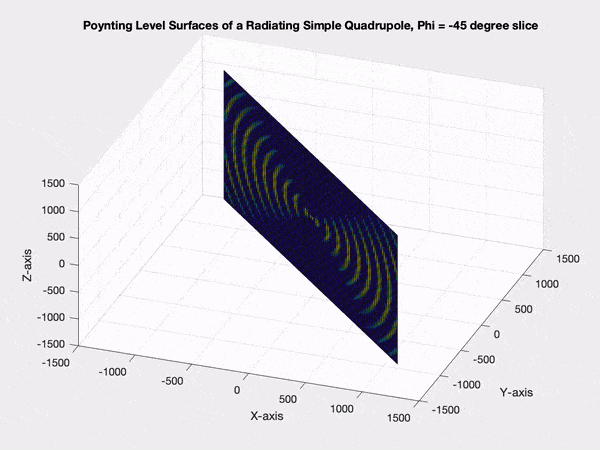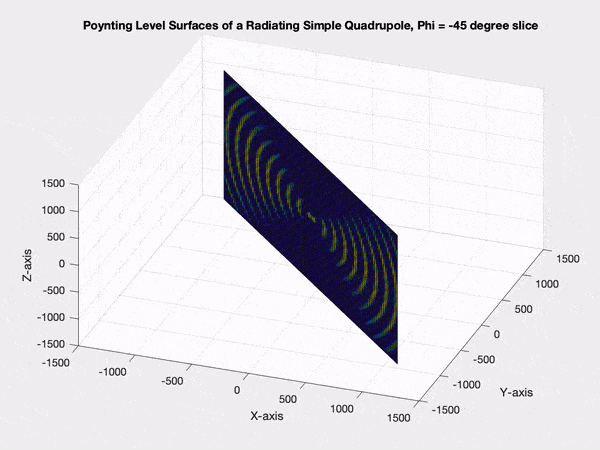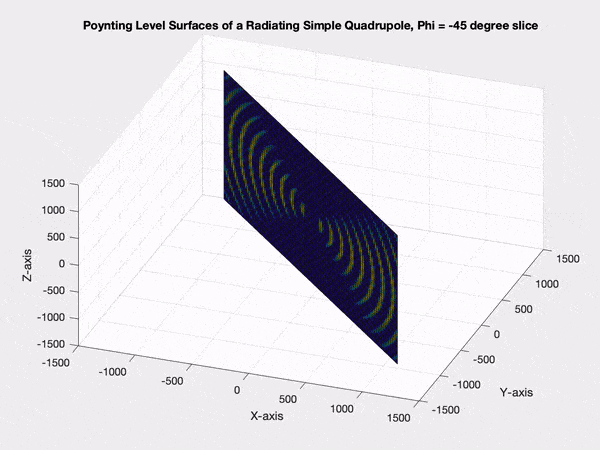
I've never worked with magnetic quadrupoles. Jackson doesn't appear to give any explicit expressions for magnetic quadrupole moments. I did find the following expression in Morse and Feshbach's Methods of Mathematical Physics for a general distribution of current density $\vec J$:

$\mathbf{M} = \frac{1}{2}\int\left[ \vec r (\vec r \times \vec J) + (\vec r \times \vec J) \vec r \right] d^3r$

This is dyadic notation. Thus to get ${M}_{xy}$, you dot the integrand from the left with a unit vector in the x-direction and dot the integrand from the right with a unit vector in the y-direction. So,

$M_{xy} = \frac{1}{2} \int \left[x(zJ_x-xJ_z) + (yJ_z-zJ_y)y\right]d^3r$
$\,\,\,\,\,\,\,\,\,\,\,\,= \frac{1}{2} \int \left[ (y^2-x^2)J_z + xzJ_x - yzJ_y \right] d^3x$

$M_{zz} = \int \left( zxJ_y - zyJ_x \right) d^3r$

etc.

The dimensions of $M$ are current times distance cubed; whereas, the dimensions of your expression for $M_{ij}$ are current times distance to the fourth.

I applied this dyadic definition to the case of a magnetic quadrupole formed from two current loops with opposite currents.

I got the same result for the magnetic quadrupole moment components as given in this link. See pages 9 through 11. The final result is at the bottom of page 11.

The vector potential $\mathbf A$ produced by this quadrupole is given by the last term shown in the equation at the top of page 11. But this is only for the far field. I would imagine that the near field would be very tedious to work out.

 

[PhDeezNutz]

Dyadic notation is something that is new to me. But it seems like I must learn it if I am to create a gif of the radiating magnetic quadrupole/electric octupole.

I truly would be lost without you.

Thank you very very much.