Preventing a block from sliding down a frictionless inclined plane

[yesmale4]

Homework Statement

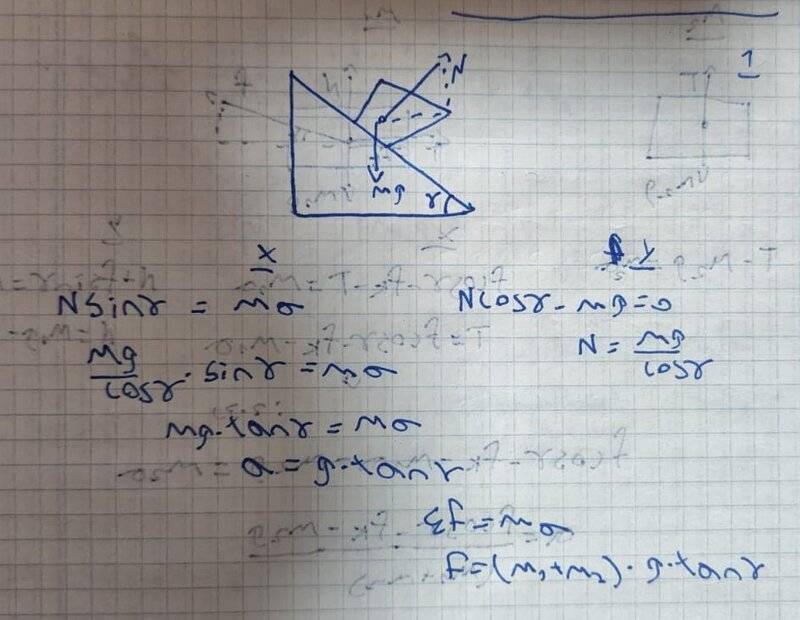
A block of mass 1.8 kg is placed on a frictionless inclined ramp of mass 12.8 kg, with the angle
θ= 34 as shown below.
Calculate the size of the net horizontal force that must be applied to the ramp to prevent the block from accelerating with respect to the ramp?

Relevant Equations

F=ma

hey i would like to understand something, i solve this question but i don't understand why my answer is right, first of all we learn that in problems like this we need to disassemble into components the mg and that what i try to do here but i didnt get the right answer so then i try to do same but this time on the N (normal) and i was correct i add my answer and i hope for some explanations

 

[PeroK]

It's not clear what you don't understand. Personally, I would use a reference frame accelerating to the right with acceleration $a$. In this frame, we have fictitious forces of $-ma$ and $-Ma$ on both masses, along with gravity and the normal forces. These forces must balance on both masses for relative equilibrium between the blocks.

 

[Orodruin]

I’ll add this to @PeroK ’s reply:

You can do this problem relatively simply by noting that the total of gravitational force and the fictitious force on the block must be perpendicular to the ramp (otherwise they cannot exactly cancel the normal force from the ramp and you won’t have equilibrium). There will be only one acceleration $a$ for which this is the case. The force on the block will be whatever force is necessary to give the full system this acceleration.

 

[kuruman]

hey, here is why your answer is right.

Your analysis is based on the fact that since the normal force $N$ is the only force acting on the block of mass $m_1$ in the horizontal direction, it is the net horizontal force on it and is therefore responsible for its acceleration $a$. Here is a streamlined version of how to put it together in the inertial frame of the surface on which the motion takes place.

1. In vertical direction, the block of mass m₁ has zero acceleration so its weight must be balanced by the vertical component of the normal force. This gives $N\cos\!\gamma=m_1g.$
2. In the horizontal direction the acceleration is $a$, therefore $N \sin\!\gamma=m_1a$.
3. Finally, since the two masses accelerate as one and the net force on the system of two masses is $F$, it follows that $F=(m_1+m_2)a$.

This gives a system of 3 equations and 3 unknowns, $N$, $a$ and $F$, which you have solved to find $F$. On your way there, you also found $N$ and $a$ in terms of the given quantities.

A word of caution: If you have more than one masses, use subscripts, else you might get hopelessly confused if the problem is more involved than this.

On edit: Modified the text to clarify it according to @Orodruin's suggestion in #5.

 

[Orodruin]

Your analysis is based on the fact that since the normal force N is the only force acting on the block of mass m1,

... in the horizontal direction. Important distinction.

A word of caution: If you have more than one masses, use subscripts, else you might get hopelessly confused if the problem is more involved than this.

It seems to me that the notation is given by the problem formulation. OP can hardly be faulted for this.

 

[Steve4Physics]

... but i didnt get the right answer so then i try ...

If you want to know why you originally got the wrong answer, you need to post the working which gave the wrong answer.

Identifying and understanding mistakes is an important part of learning.