MatinSAR
- 673
- 204
- Homework Statement
- Suppose you are walking next to a flowing river. Is it possible for you to see that the river is still?
- Relevant Equations
- Relative motion.
My attemp :
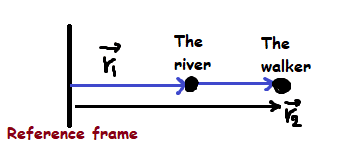
##\vec r_1## : Position of the river in reference frame.
##\vec r_2## : Position of the walker in reference frame.
##\vec r_x## : Position of the walker measured by the river.
We have: $$\vec r_1 + \vec r_x = \vec r_2$$ $$\vec v = \dfrac {d \vec r}{dt} $$ $$\vec v_1 + \vec v_x = \vec v_2$$ $$\vec v_x = \vec v_2 - \vec v_1$$
So if the river and the walker are moving is same direction with same speed then the walker sees that the river is still.
##\vec r_1## : Position of the river in reference frame.
##\vec r_2## : Position of the walker in reference frame.
##\vec r_x## : Position of the walker measured by the river.
We have: $$\vec r_1 + \vec r_x = \vec r_2$$ $$\vec v = \dfrac {d \vec r}{dt} $$ $$\vec v_1 + \vec v_x = \vec v_2$$ $$\vec v_x = \vec v_2 - \vec v_1$$
So if the river and the walker are moving is same direction with same speed then the walker sees that the river is still.
Last edited: