russel_
- 7
- 0
Jeronimus said:(and much closer to the value you hoped for)
Except that the value I was hoping & arguing for was 4.8, you may have missed the different usernames?
Jeronimus said:(and much closer to the value you hoped for)
If I understand the problem statement right, A emits the pulse when he is 4.8ly distant from B as measured in B's frame. This is the time B is calling zero, so obviously, B's clock will read 4.8 years when he receives the pulse. This is 3.2 years before the two ships meet up, which happens at 8 years on B's clock.russel_ said:Well, the "synced at t=0" statement wasn't in the original (pre-forum) problem statement, so in this regard I claim innocence :).
russel_ said:- it claims to "explain" the twin paradox in terms of the time it takes for light to reach each observer. Now I claimed that this is misleading, because while the time delays might be interesting to consider in terms of what you'd actually "see", they are not relevant to the effects derived in Special Relativity. That is, time dilation and other effects are "real" and not just tricks due to how long it takes light to reach observers from distance events.
Mister T said:But the delay due to light travel time is not a trick, it's real and to understand it you need to account for time dilation. You might gain some insight by reviewing the short and simple derivation of the relativistic Doppler effect. In the example cited ##\beta=0.6## so we have for the reativistic Doppler effect factor $$\sqrt{\frac{1+\beta}{1-\beta}}=\sqrt{\frac{1+0.6}{1-0.6}}=\sqrt{\frac{1.6}{1-0.6}}=2.$$ Thus each twin sees the other's clock running fast (or slow) by factor of 2 when they are approaching (or receding from) each other.
Search for Hewitt's Twin Trip on YouTube. He uses the same speed of ##0.6 c## in his example, but instead of watching each other's clock, the twins send each other pulses of light.
Mister T said:But the delay due to light travel time is not a trick, it's real and to understand it you need to account for time dilation.
Ibix said:Actually, you can adjust time dilation freely by changing your interpretation of what causes the Doppler effect. You can't make the Doppler effect go away, nor can you make differential aging (as in the twin paradox) go away. In some senses they are more fundamental than time dilation and length contraction.
Orodruin said:No. You are still failing to specify what "at the same time" means as requested in #2. You need this to give the problem meaning.
You can do this in several ways, for example:
When the distance between A and B in A's reference frame is 6 light-years, A sends a signal to B. What is the time difference between this event and B receiving the signal in the reference frame of B?
Alternatively:
When the distance between A and B in A's reference frame is 6 light-years, A sends a signal to B. What is the time difference in the reference frame of B between the event on the world line of B that is simultaneous with the sending of the signal in A's rest frame and the event of B receiving the signal?
These are different questions with different answers.
There is no such thing as a "stationary" reference frame. Reference frames can only be moving or at rest relative to some object or other reference frame. This is true in classical mechanics as well as SR.
Yes.david316 said:In A's frame of reference, when B is 6 light-years away, A sends a photon to B.
What is the time difference in the reference frame of B between the event on the world line of B that is simultaneous with the sending of the signal in A's rest frame and the event of B receiving the signal?
Answer = 3 years ... (i hope)
3.75 years (##\gamma## times your last answer).david316 said:What is the time difference in the reference frame of A between the sending of the signal in A's rest frame and the event on the world line of A that is simultaneous with the event of B receiving the signal?
Answer = 6 years ... (i hope)
Yes.david316 said:In A's frame of reference, when B is 6 light-years away, A sends a photon to B. What is the time difference between this event and B receiving the signal in the reference frame of B?
Answer = 7.5 years ... (i hope)
Make sense. Thanks.Ibix said:Yes.
3.75 years (##\gamma## times your last answer).
Yes.
david316 said:What is the time difference in the reference frame of A between the sending of the signal in A's rest frame and the event on the world line of A that is simultaneous with the event of B receiving the signal?
Answer = 6 years ... (i hope)
The easier way of seeing this is: The distance between B and the signal decreases at speed 1.6c and so the result is 6/1.6 = 3.75 years. Everything in the problem refers to frame A and so there is no reason to involve anything from B (except its velocity relative to A).Ibix said:3.75 years (γγ\gamma times your last answer).
david316 said:Thank you Orodruin for your phasing of the two questions and you subsequent answers. They clarified how I should be posing the question. Would below be a better way to phase it?
Two observers, A and B, are traveling towards each other at a relative speed of 0.6c.
In A's frame of reference, when B is 6 light-years away, A sends a photon to B.
What is the time difference in the reference frame of B between the event on the world line of B that is simultaneous with the sending of the signal in A's rest frame and the event of B receiving the signal?
Answer = 3 years ... (i hope)
What is the time difference in the reference frame of A between the sending of the signal in A's rest frame and the event on the world line of A that is simultaneous with the event of B receiving the signal?
Answer = 6 years ... (i hope)
In A's frame of reference, when B is 6 light-years away, A sends a photon to B. What is the time difference between this event and B receiving the signal in the reference frame of B?
Answer = 7.5 years ... (i hope)
russel_ said:That isn't what I said - I didn't say the light travel time wasn't real or is a trick, I said time dilation itself is real and not a trick - there is a logical difference. I understand the article wasn't exactly denying that either but I just said it could be misleading - in the sense that it could lead people to that conclusion if they didn't already know better. I don't know how that wasn't clear.
Ibix said:Actually, you can adjust time dilation freely by changing your interpretation of what causes the Doppler effect. You can't make the Doppler effect go away, nor can you make differential aging (as in the twin paradox) go away. In some senses they are more fundamental than time dilation and length contraction.
david316 said:Thank you Orodruin for your phasing of the two questions and you subsequent answers. They clarified how I should be posing the question. Would below be a better way to phase it?
Two observers, A and B, are traveling towards each other at a relative speed of 0.6c.
In A's frame of reference, when B is 6 light-years away, A sends a photon to B.
What is the time difference in the reference frame of B between the event on the world line of B that is simultaneous with the sending of the signal in A's rest frame and the event of B receiving the signal?
Answer = 3 years ... (i hope)
What is the time difference in the reference frame of A between the sending of the signal in A's rest frame and the event on the world line of A that is simultaneous with the event of B receiving the signal?
Answer = 6 years ... (i hope)
In A's frame of reference, when B is 6 light-years away, A sends a photon to B. What is the time difference between this event and B receiving the signal in the reference frame of B?
Answer = 7.5 years ... (i hope)
And a final question:
Two observers, A and B, are traveling relative to each other at a relative speed of 0.6c.
In A's frame of reference, there is a ruler that is 4.8 light years long.
In A's frame of reference how long would it take a photon of light to travel the length of the ruler?
Answer = 4.8 years ... ( I hope)
In B's frame of reference there is a ruler. Said ruler measures 4.8 light long in A frame's of reference. How long would it take a photon to travel the length of the ruler in B's frame of reference?
Answer = 6 years ... (i hope... still feeling shaky)
russel_ said:In the interests of clarifying things, and saving my sanity, I thought I'd offer some background on how this problem came about and hopefully clarify where the ambiguities may have been introduced.
It all started when this Scientific American article (https://www.scientificamerican.com/article/time-and-the-twin-paradox-2006-02/) came up in discussion - it claims to "explain" the twin paradox in terms of the time it takes for light to reach each observer. Now I claimed that this is misleading, because while the time delays might be interesting to consider in terms of what you'd actually "see", they are not relevant to the effects derived in Special Relativity. That is, time dilation and other effects are "real" and not just tricks due to how long it takes light to reach observers from distance events.
Mister T said:Consider the event "traveler arrives at star" and the event "home clock reads 10 years". Saying that the first one happened when the second one happened is not a meaningful assertion. The two events occur in different places, so if they're simultaneous to one of the twins they won't be simultaneous to the other.
If, however, the two events occur at the same place, then such a statement is meaningful. Because it will be true for all observers.
david316 said:Is the statement below correct, in the context of SR not GR ... I'm not liking my odds...
"Two people will only disagree on the time of a single clock if you limit information travel by the speed of light and one person is traveling relative to the other. "
russel_ said:I suspect someone will take exception to the notion of a "single clock"! I say this because the observers have different clocks (different frames), and while a single event could be used to set both to "0", I don't think that really gets at the matter. Maybe the statement below would be as good? Here the "clock" is replaced with an event, and you need two of them so the observers can make a comparison (i.e., the spacing and coincidence of events is what defines our underlying notion of time).
"Two people will only disagree on the simultaneity of two events at different locations if you limit information travel by the speed of light and one person is traveling relative to the other."
And I hazard to say that, at least as I understand it, this is not true: they can disagree even after taking into account the time it took the information to travel. They literally observe (not just "see") parts of space arriving at various times differently than the other does. We'll see what others say...
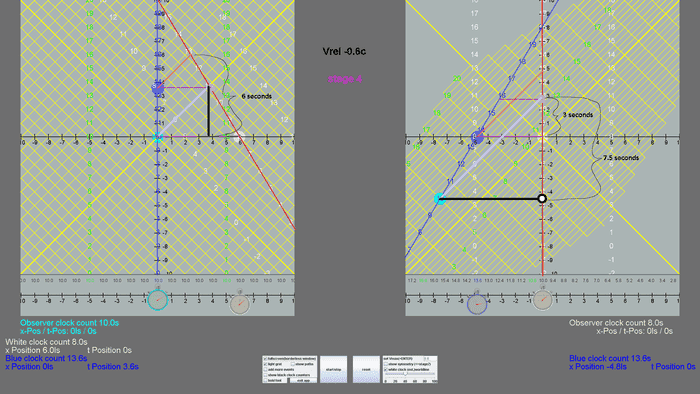
Jeronimus said:Here is a more complete drawing of the situation, which will hopefully shed some light on this
david316 said:Yip. In my sleep deprived state I think I agree with what you think I think. i.e.
"In the framework of special relativity, two people will only disagree on the simultaneity of two events at different locations if you limit information travel by the speed of light and one person is traveling relative to the other."
I still think this true but I accept my knowledge in this area has been proved to be vastly lacking and hence won't be surprised if its wrong!
robphy said:The relative velocity on the left looks like 6/10.
The relative velocity on the right looks like 5/8... is that what you want?
Jeronimus said:Two observers traveling at ANY given speed relative to each other, will NEVER agree on the simultaneity of two space separated events. If observer A observers two events to be simultaneous, hence their spacetime location withing his reference frame is x1, t1 and x2, t2 with x1 ≠ x2 (space separated) and t1=t2 (simultaneous), THEN observer B will _always_ get t1' ≠ t2' (NOT-simultaneous).
So if observer A checks his clock, and his clock displays whatever count. Let's assume 0 as you seem to like that number. At the same time, A observes B's clock to show 0 THEN observer B will never ever for eternity observe his clock to display a count of 0 while A's clock displays 0 as well. (unless the clocks are damaged or drugs were involved)
When we say observe, we mean measure the incoming information we get locally and then calculate the spacetime positions of events based on this information. If for example a light beam reaches us, then we can calculate the spacetime location of when and where the lightbeam was shot towards us, given we get the maths and physics right and we have sufficient additional information.
Or, if you follow Einstein. We would place an infinite amount of observers at every location, collect the event data they registered after some time, and then create some nice spacetime diagrams we would map all spacetime events they registered within it.
Observation is not about what we see, but about what we measure and calculate.
david316 said:And as I believe you implied above, if two observers somehow knew the spacetime location of an event in each others frame of reference and they know their relative speed, they could both agree at what space time location the event occurred in each others location.
david316 said:Can I re-phase the statement.
"Two people traveling relative to each other will disagree on the simultaneity of two events at different locations. The fundamental principe underlying this is that the speed of light is constant in all frames of reference."
And as I believe you implied above, if two observers somehow knew the spacetime location of an event in each others frame of reference and they know their relative speed, they could both agree at what space time location the event occurred in each others location.
Jeronimus said:Yes, and that is what the Lorentz transformations are about. Their basic forms are very simple too.
The Lorentz transformation formulas to get x' and t' are
x' = γ(x-vt)
t' = γ(t-vx/c2)
to get back, you would use the inverse Lorentz transformations formulas
x = γ(x'+vt')
t = γ(t'+vx'/c2)
γ=1/(√1-v2/c2) = 1.25 for v=0.6c
x: space position of event (where is it located)
t: time position of event (when does it happen)
v: The relative velocity
c: The speed of light
see more here https://en.wikipedia.org/wiki/Lorentz_transformation
Those formulas can be derived mathematically just by the two postulates of SR
1) The laws of physics are the same in every inertial frame of reference (no IFR is special compared to another)
2) The speed of light is always c in a vacuum absent of gravity (independent on which inertial frame of reference frame you observe a beam of light, you will always observe it traveling at c, independent of the velocity of the emitting source)
(note that the formulas also depend on where you choose to locate the positive and negative x-axis within the two reference frames/coordinate systems)
And just by knowing how to apply those formulas, you can create the simulation of the twin paradox i programmed, i already linked at an earlier post. Scroll back if you missed it or click here https://www.physicsforums.com/threads/second-opinion-needed.906688/page-3#post-5710416
Try to apply the formulas by taking any event x, t on the left x-t diagram in my simulation at any time you wish and then see if you get the right x', t' values for the right diagram for the event.
Take an event in the right x-t diagram of my simulation and apply the inverse Lorentz transformation formulas and see if it maps properly in the left diagram.
For example, let's take the white filled circle in the screenshot i made.
It is located at x=6ls, t=0s in the left diagram
x' = 1.25*(6ls - (-0.6c)*0) = 7.5ls
t' = 1.25*(0 - (-0.6c)*6ls/c2) = 4.5s (you won't have to deal with c2 as -0.6c*6cs (lightsecond/ls) /c2 shortens to -0.6*6s)
Now that makes me look like a liar, because in the right diagram, the white filled circle is always located at x=0, t=0 (or x'=0 , t'=0 if you wanted to be in accord with how this is usually defined - in my simulation it is x and t for both sides)
But that is intentionally. The observer in the right diagram can always draw the x-t diagram such that he is in the middle, and map all events relative to that.
Check where the teal filled circle is in the right diagram. It is at x' = -7.5ls, t' = -4.5ls
So i could have drawn the right x-t diagram such that the teal circle is at x'=0, t'=0 and instead the white circle would be at x' =7.5ls and t'=4.5s as calculated with the Lorentz transformations but since i wanted to draw it from the perspective of the traveling twin, hence him mapping all events relative to him as he "travels", this seemed the more appropriate way to do the simulation.
Think of the right diagram as the traveling twin (white filled circle) drawing x-t diagrams periodically along his travel. In those x-t diagrams he maps the spacetime location of every event relative to himself while placing himself at x=0, t=0 within the diagram.
Afterwards he creates an video animation of those diagrams. The right diagram is what you would get.
And that is all you need basically to create the simulation i created. That, and some petty coding skills like mine, willing to stare at code for hours without writing a line.
david316 said:So for example. If there are two observers in the same rest frame. Both with clocks that are synced. One observer instantly accelerates to 0.6c (I know this isn't possible but humour me). The clock signals are sent between the observers at the speed of light. When one observer receives a clock signal he can derive what the other observer will be seeing on their clock at the event on the other observers world line that is simultaneous with when said observer receives clock signal. e.g. When observer A receives a clock signal he can derive what observer B will be seeing on their clock at the event on observers B world line that is simultaneous with when observer A receives the clock signal. This calculation will give observer A the correct time that observer B will be seeing on their clock at the event on observers B world line that is simultaneous with observer A receiving said clock signal.
This is only true in 1+1 space-time dimensions. In 1+3, it is true if you make the separation along the relative direction of motion non-zero. (In 1+1 there is only one spatial direction to move in.)Jeronimus said:Two observers traveling at ANY given speed relative to each other, will NEVER agree on the simultaneity of two space separated events
david316 said:So for example. If there are two observers in the same rest frame. Both with clocks that are synced. One observer instantly accelerates to 0.6c (I know this isn't possible but humour me).
The clock signals are sent between the observers at the speed of light. When one observer receives a clock signal he can derive what the other observer will be seeing on their clock at the event on the other observers world line that is simultaneous with when said observer receives clock signal. e.g. When observer A receives a clock signal he can derive what observer B will be seeing on their clock at the event on observers B world line that is simultaneous with when observer A receives the clock signal. This calculation will give observer A the correct time that observer B will be seeing on their clock at the event on observers B world line that is simultaneous with observer A receiving said clock signal.
Mister T said:Just have the two observers pass each at speed ##0.6c## and agree to synchronize their clocks when they do so.
Mister T said:You mean A sends a light signal and B receives the signal. B can then figure out what B's clock must have read when A sent the signal.
And of course A will not agree with B. A will conclude that B's clock had a different reading when A sent the signal. It is not the clock-readings themselves that they disagree on. All they disagree on is the notion of "when".
david316 said:After some arbitrary distance A sends a light signal to B.
When B receives the signal he can use the maths of Lorentz transformation to figure out what A's clock would have read.
A will agree that his clock read what B calculated.