Second Opinion Needed: Time of Light Pulse Arrival

[robphy]

Here is a more complete drawing of the situation, which will hopefully shed some light on this

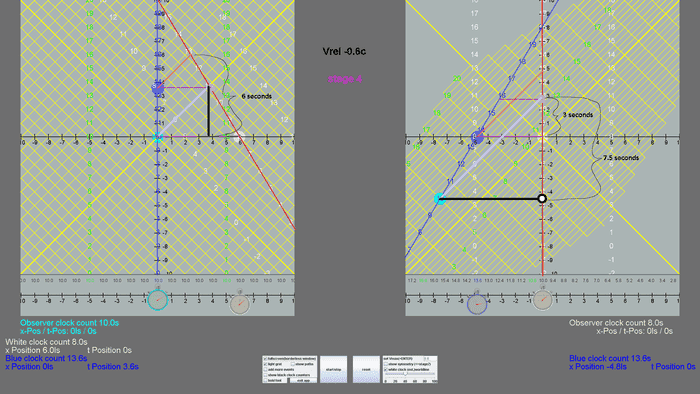
The relative velocity on the left looks like 6/10.
The relative velocity on the right looks like 5/8... is that what you want?

 

[Jeronimus]

Yip. In my sleep deprived state I think I agree with what you think I think. i.e.

"In the framework of special relativity, two people will only disagree on the simultaneity of two events at different locations if you limit information travel by the speed of light and one person is traveling relative to the other."

I still think this true but I accept my knowledge in this area has been proved to be vastly lacking and hence won't be surprised if its wrong!

Two observers traveling at ANY given speed relative to each other, will NEVER agree on the simultaneity of two space separated events. If observer A observers two events to be simultaneous, hence their spacetime location withing his reference frame is x1, t1 and x2, t2 with x1 ≠ x2 (space separated) and t1=t2 (simultaneous), THEN observer B will _always_ get t1' ≠ t2' (NOT-simultaneous).

So if observer A checks his clock, and his clock displays whatever count. Let's assume 0 as you seem to like that number. At the same time, A observes B's clock to show 0 THEN observer B will never ever for eternity observe his clock to display a count of 0 while A's clock displays 0 as well. (unless the clocks are damaged or drugs were involved)

When we say observe, we mean measure the incoming information we get locally and then calculate the spacetime positions of events based on this information. If for example a light beam reaches us, then we can calculate the spacetime location of when and where the lightbeam was shot towards us, given we get the maths and physics right and we have sufficient additional information.
Or, if you follow Einstein. We would place an infinite amount of observers at every location, collect the event data they registered after some time, and then create some nice spacetime diagrams we would map all spacetime events they registered within it.

Observation is not about what we see, but about what we measure and calculate.

 

[Jeronimus]

The relative velocity on the left looks like 6/10.
The relative velocity on the right looks like 5/8... is that what you want?

Not. That would be a disaster if it was the case.

But i don't think it is.

The white observer in the left x-t diagram at the spacetime location x=6ls t=0s will be crossing the t axis in 10 seconds according to the diagram. So we have 6ls /10s = 0.6c

The Blue clock in the right diagram is located at x=-4.8ls, t = 0 and will be crossing the t axis within 8 seconds as you can see from its worldline. -4.8ls/8s = -0.6c

Looks good to me.

 

[david316]

Two observers traveling at ANY given speed relative to each other, will NEVER agree on the simultaneity of two space separated events. If observer A observers two events to be simultaneous, hence their spacetime location withing his reference frame is x1, t1 and x2, t2 with x1 ≠ x2 (space separated) and t1=t2 (simultaneous), THEN observer B will _always_ get t1' ≠ t2' (NOT-simultaneous).

So if observer A checks his clock, and his clock displays whatever count. Let's assume 0 as you seem to like that number. At the same time, A observes B's clock to show 0 THEN observer B will never ever for eternity observe his clock to display a count of 0 while A's clock displays 0 as well. (unless the clocks are damaged or drugs were involved)

When we say observe, we mean measure the incoming information we get locally and then calculate the spacetime positions of events based on this information. If for example a light beam reaches us, then we can calculate the spacetime location of when and where the lightbeam was shot towards us, given we get the maths and physics right and we have sufficient additional information.
Or, if you follow Einstein. We would place an infinite amount of observers at every location, collect the event data they registered after some time, and then create some nice spacetime diagrams we would map all spacetime events they registered within it.

Observation is not about what we see, but about what we measure and calculate.

Can I re-phase the statement.

"Two people traveling relative to each other will disagree on the simultaneity of two events at different locations. The fundamental principe underlying this is that the speed of light is constant in all frames of reference."

And as I believe you implied above, if two observers somehow knew the spacetime location of an event in each others frame of reference and they know their relative speed, they could both agree at what space time location the event occurred in each others location.

 

[Mister T]

And as I believe you implied above, if two observers somehow knew the spacetime location of an event in each others frame of reference and they know their relative speed, they could both agree at what space time location the event occurred in each others location.

By spacetime location do you mean spacetime coordinates? For example, an event occurred at t=5 and x=2 in my rest frame, and the same event occurred at t'=3 and x'=0 in your rest frame? Regardless of our relative speed we will both agree on all of that.

 

[Jeronimus]

Can I re-phase the statement.

"Two people traveling relative to each other will disagree on the simultaneity of two events at different locations. The fundamental principe underlying this is that the speed of light is constant in all frames of reference."

And as I believe you implied above, if two observers somehow knew the spacetime location of an event in each others frame of reference and they know their relative speed, they could both agree at what space time location the event occurred in each others location.

Yes, and that is what the Lorentz transformations are about. Their basic forms are very simple too.

The Lorentz transformation formulas to get x' and t' are

x' = γ(x-vt)
t' = γ(t-vx/c²)

to get back, you would use the inverse Lorentz transformations formulas

x = γ(x'+vt')
t = γ(t'+vx'/c²)

γ=1/(√1-v²/c²) = 1.25 for v=0.6c

x: space position of event (where is it located)
t: time position of event (when does it happen)
v: The relative velocity
c: The speed of light

see more here https://en.wikipedia.org/wiki/Lorentz_transformation

Those formulas can be derived mathematically just by the two postulates of SR

1) The laws of physics are the same in every inertial frame of reference (no IFR is special compared to another)
2) The speed of light is always c in a vacuum absent of gravity (independent on which inertial frame of reference frame you observe a beam of light, you will always observe it traveling at c, independent of the velocity of the emitting source)

(note that the formulas also depend on where you choose to locate the positive and negative x-axis within the two reference frames/coordinate systems)

And just by knowing how to apply those formulas, you can create the simulation of the twin paradox i programmed, i already linked at an earlier post. Scroll back if you missed it or click here https://www.physicsforums.com/threads/second-opinion-needed.906688/page-3#post-5710416
Try to apply the formulas by taking any event x, t on the left x-t diagram in my simulation at any time you wish and then see if you get the right x', t' values for the right diagram for the event.

Take an event in the right x-t diagram of my simulation and apply the inverse Lorentz transformation formulas and see if it maps properly in the left diagram.

For example, let's take the white filled circle in the screenshot i made.

It is located at x=6ls, t=0s in the left diagram

x' = 1.25*(6ls - (-0.6c)*0) = 7.5ls
t' = 1.25*(0 - (-0.6c)*6ls/c²) = 4.5s (you won't have to deal with c² as -0.6c*6cs (lightsecond/ls) /c² shortens to -0.6*6s)

Now that makes me look like a liar, because in the right diagram, the white filled circle is always located at x=0, t=0 (or x'=0 , t'=0 if you wanted to be in accord with how this is usually defined - in my simulation it is x and t for both sides)

But that is intentionally. The observer in the right diagram can always draw the x-t diagram such that he is in the middle, and map all events relative to that.

Check where the teal filled circle is in the right diagram. It is at x' = -7.5ls, t' = -4.5ls

So i could have drawn the right x-t diagram such that the teal circle is at x'=0, t'=0 and instead the white circle would be at x' =7.5ls and t'=4.5s as calculated with the Lorentz transformations but since i wanted to draw it from the perspective of the traveling twin, hence him mapping all events relative to him as he "travels", this seemed the more appropriate way to do the simulation.

Think of the right diagram as the traveling twin (white filled circle) drawing x-t diagrams periodically along his travel. In those x-t diagrams he maps the spacetime location of every event relative to himself while placing himself at x=0, t=0 within the diagram.
Afterwards he creates an video animation of those diagrams. The right diagram is what you would get.

And that is all you need basically to create the simulation i created. That, and some petty coding skills like mine, willing to stare at code for hours without writing a line.

 

[david316]

Yes, and that is what the Lorentz transformations are about. Their basic forms are very simple too.

The Lorentz transformation formulas to get x' and t' are

x' = γ(x-vt)
t' = γ(t-vx/c²)

to get back, you would use the inverse Lorentz transformations formulas

x = γ(x'+vt')
t = γ(t'+vx'/c²)

γ=1/(√1-v²/c²) = 1.25 for v=0.6c

x: space position of event (where is it located)
t: time position of event (when does it happen)
v: The relative velocity
c: The speed of light

see more here https://en.wikipedia.org/wiki/Lorentz_transformation

Those formulas can be derived mathematically just by the two postulates of SR

1) The laws of physics are the same in every inertial frame of reference (no IFR is special compared to another)
2) The speed of light is always c in a vacuum absent of gravity (independent on which inertial frame of reference frame you observe a beam of light, you will always observe it traveling at c, independent of the velocity of the emitting source)

(note that the formulas also depend on where you choose to locate the positive and negative x-axis within the two reference frames/coordinate systems)

And just by knowing how to apply those formulas, you can create the simulation of the twin paradox i programmed, i already linked at an earlier post. Scroll back if you missed it or click here https://www.physicsforums.com/threads/second-opinion-needed.906688/page-3#post-5710416
Try to apply the formulas by taking any event x, t on the left x-t diagram in my simulation at any time you wish and then see if you get the right x', t' values for the right diagram for the event.

Take an event in the right x-t diagram of my simulation and apply the inverse Lorentz transformation formulas and see if it maps properly in the left diagram.

For example, let's take the white filled circle in the screenshot i made.

It is located at x=6ls, t=0s in the left diagram

x' = 1.25*(6ls - (-0.6c)*0) = 7.5ls
t' = 1.25*(0 - (-0.6c)*6ls/c²) = 4.5s (you won't have to deal with c² as -0.6c*6cs (lightsecond/ls) /c² shortens to -0.6*6s)

Now that makes me look like a liar, because in the right diagram, the white filled circle is always located at x=0, t=0 (or x'=0 , t'=0 if you wanted to be in accord with how this is usually defined - in my simulation it is x and t for both sides)

But that is intentionally. The observer in the right diagram can always draw the x-t diagram such that he is in the middle, and map all events relative to that.

Check where the teal filled circle is in the right diagram. It is at x' = -7.5ls, t' = -4.5ls

So i could have drawn the right x-t diagram such that the teal circle is at x'=0, t'=0 and instead the white circle would be at x' =7.5ls and t'=4.5s as calculated with the Lorentz transformations but since i wanted to draw it from the perspective of the traveling twin, hence him mapping all events relative to him as he "travels", this seemed the more appropriate way to do the simulation.

Think of the right diagram as the traveling twin (white filled circle) drawing x-t diagrams periodically along his travel. In those x-t diagrams he maps the spacetime location of every event relative to himself while placing himself at x=0, t=0 within the diagram.
Afterwards he creates an video animation of those diagrams. The right diagram is what you would get.

And that is all you need basically to create the simulation i created. That, and some petty coding skills like mine, willing to stare at code for hours without writing a line.

So for example. If there are two observers in the same rest frame. Both with clocks that are synced. One observer instantly accelerates to 0.6c (I know this isn't possible but humour me). The clock signals are sent between the observers at the speed of light. When one observer receives a clock signal he can derive what the other observer will be seeing on their clock at the event on the other observers world line that is simultaneous with when said observer receives clock signal. e.g. When observer A receives a clock signal he can derive what observer B will be seeing on their clock at the event on observers B world line that is simultaneous with when observer A receives the clock signal. This calculation will give observer A the correct time that observer B will be seeing on their clock at the event on observers B world line that is simultaneous with observer A receiving said clock signal.

 

[Jeronimus]

So for example. If there are two observers in the same rest frame. Both with clocks that are synced. One observer instantly accelerates to 0.6c (I know this isn't possible but humour me). The clock signals are sent between the observers at the speed of light. When one observer receives a clock signal he can derive what the other observer will be seeing on their clock at the event on the other observers world line that is simultaneous with when said observer receives clock signal. e.g. When observer A receives a clock signal he can derive what observer B will be seeing on their clock at the event on observers B world line that is simultaneous with when observer A receives the clock signal. This calculation will give observer A the correct time that observer B will be seeing on their clock at the event on observers B world line that is simultaneous with observer A receiving said clock signal.

I won't try to fully decipher this because it might blow my mind. But i believe i know what you are trying to understand, so i will give you an example more or less based on the above.

Two observers, A and B are at rest relative to each other. B is 5 lightseconds away of B. Their clocks are synced, let's say that both display 0 seconds.

To keep it simple, We place A in the middle of our x-t diagram, hence A's spacetime location is x1=0ls, t1=0s while B is located at x2= 5ls, t2=0s. Both their clock counts display 0 seconds at those spacetime locations.
B located at x=5ls, t=0s with a clock count of 0s is an event. Let's call this event E2.

Now A accelerates near instantaneously to 0.6c. What will be the clock count on B's clock he will observe post-acceleration?

First let's check where the instance of B with a clock count of 0 seconds will be located post-acceleration as measured/calculated by A.

x' = γ(x-vt)
t' = γ(t-vx/c²)

γ=1/(√1-v²/c²) = 1.25 for v=0.6c

so we get

x' = 1.25*(5ls-0.6c*0s) = 6.25ls
t' = 1.25(0-0.6*5s) = -3.75s

So for A who accelerated to 0.6c near instantaneously, the instance of B with a clock count of 0s now has a spacetime position of x'=6.25ls and t'= -3.75s . This instance of B is not simultaneous to A anymore. Let's call this event E2'

We might want to know which instance of B is simultaneous to A now.

Let's see what we have. We have t' =0 (the time location of the instance of B in A's rest frame), γ = 1.25, v=0.6c, x=5ls (the location of B in B's rest frame - All instances of B are located at x=5ls in B's rest frame... he stays at 5ls at all times obviously)

using t' = γ(t-vx/c²) and solving for t, we get:

t= t'/γ + vx/c² = 3s - That gives us the time location of the instance of B in B's rest frame, which A will observe to be at t'=0 (simultaneous). This also tells us that the clock count of this instance of B will be 3 seconds at this location.
In B's rest frame, this instance is located at x=5ls, t=3s with a clock count of 3s. Let's call this event E1.

Now that we have the time location of the instance we are looking for, we can solve for x'. We already have t'=0.

x' = γ(x-vt) = 1.25(5ls-0.6c*3s) = 4ls

So now we know, that A will observe the instance of B which is simultaneous to him, to be at x' = 4ls, t' =0s with a clock count of 3 seconds. This is event E1'

But let's see what the simulation tells us

check if the calculations match the screenshot of the simulation, download and run the simulation yourself (remember to enter 0.6c as Vmax before you start it)

I

 

[Orodruin]

Two observers traveling at ANY given speed relative to each other, will NEVER agree on the simultaneity of two space separated events

This is only true in 1+1 space-time dimensions. In 1+3, it is true if you make the separation along the relative direction of motion non-zero. (In 1+1 there is only one spatial direction to move in.)

 

[Mister T]

So for example. If there are two observers in the same rest frame. Both with clocks that are synced. One observer instantly accelerates to 0.6c (I know this isn't possible but humour me).

Just have the two observers pass each at speed $0.6c$ and agree to synchronize their clocks when they do so.

The clock signals are sent between the observers at the speed of light. When one observer receives a clock signal he can derive what the other observer will be seeing on their clock at the event on the other observers world line that is simultaneous with when said observer receives clock signal. e.g. When observer A receives a clock signal he can derive what observer B will be seeing on their clock at the event on observers B world line that is simultaneous with when observer A receives the clock signal. This calculation will give observer A the correct time that observer B will be seeing on their clock at the event on observers B world line that is simultaneous with observer A receiving said clock signal.

You mean A sends a light signal and B receives the signal. B can then figure out what B's clock must have read when A sent the signal.

And of course A will not agree with B. A will conclude that B's clock had a different reading when A sent the signal. It is not the clock-readings themselves that they disagree on. All they disagree on is the notion of "when".

 

[david316]

Just have the two observers pass each at speed $0.6c$ and agree to synchronize their clocks when they do so.

Sure.

You mean A sends a light signal and B receives the signal. B can then figure out what B's clock must have read when A sent the signal.

And of course A will not agree with B. A will conclude that B's clock had a different reading when A sent the signal. It is not the clock-readings themselves that they disagree on. All they disagree on is the notion of "when".

No. After some arbitrary distance A sends a light signal to B. When B receives the signal he can use the maths of Lorentz transformation to figure out what A's clock would have read. A will agree that his clock read what B calculated.

 

[Mister T]

After some arbitrary distance A sends a light signal to B.

Yes, that's what I was thinking, too.

When B receives the signal he can use the maths of Lorentz transformation to figure out what A's clock would have read.

Yes. But let's say that the value B calculates for A's clock-reading is $t_A$. Moreover B calculates that the reading on his own clock was $t_B$ when that signal was sent.

A will agree that his clock read what B calculated.

Yes. But A won't agree that B's clock read $t_B$ when A's clock read $t_A$.