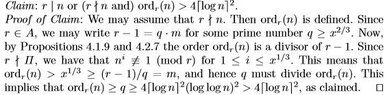- #71
evinda
Gold Member
MHB
- 3,836
- 0
Then we check how many times the while-loop is executed. There is the following lemma.
View attachment 7628
First of all, how do we get that $\Omega\left(\frac{x}{\log{x}}\right)=\Omega((\log{n})^3 (\log{\log{n}})^2)$ ?
I got that $\frac{x}{\log{x}}=\frac{8 \lceil \log{n}\rceil^3 (\log{\log{n}})^3}{\log{8}+3 \log{(\lceil \log{n}\rceil)+3 \log{(\log{\log{n}})}}}$... But is this in $\Omega((\log{n})^3 (\log{\log{n}})^2)$ ?
Also how do we get that $n^{\frac{x^{\frac{2}{3}}}{3}} <\Pi<n^{x^{\frac{2}{3}}}$ ? (Thinking)
View attachment 7628
First of all, how do we get that $\Omega\left(\frac{x}{\log{x}}\right)=\Omega((\log{n})^3 (\log{\log{n}})^2)$ ?
I got that $\frac{x}{\log{x}}=\frac{8 \lceil \log{n}\rceil^3 (\log{\log{n}})^3}{\log{8}+3 \log{(\lceil \log{n}\rceil)+3 \log{(\log{\log{n}})}}}$... But is this in $\Omega((\log{n})^3 (\log{\log{n}})^2)$ ?
Also how do we get that $n^{\frac{x^{\frac{2}{3}}}{3}} <\Pi<n^{x^{\frac{2}{3}}}$ ? (Thinking)