Guillem_dlc
- 188
- 17
- Homework Statement
- In the circuit of the figure, determine:
1. Equivalent Thévenin and Norton circuits, viewed from terminals A and B.
2. Value of the load resistance ##R_C## connected between A and B for the circuit to work at maximum power transfer conditions.
3. The power in the load resistor deduced in the previous section.
4. The power in the load resistor in the event that its value is twice that calculated in section 2.
- Relevant Equations
- Thévenin and Norton
Figure:
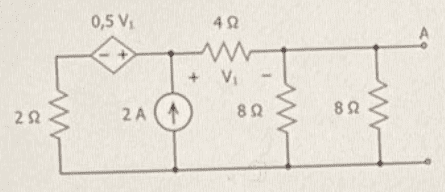
My attempt at a solution:
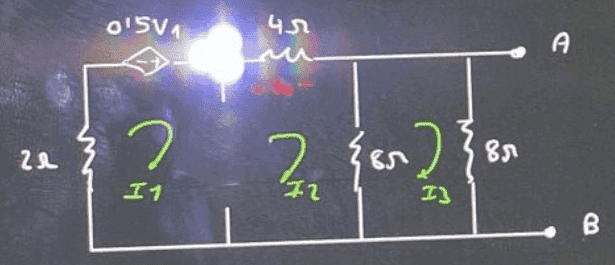
a) ##\boxed{V_{TH}}##
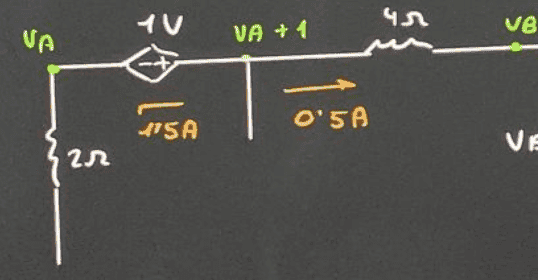
We know that ##\rightarrow V_B=V_{TH}##
$$V_A=0+1,5\cdot 2=3\, \textrm{V}$$
$$V_B=V_A+1-0,5\cdot 4=2\, \textrm{V}$$
$$\boxed{V_{TH}=2\, \textrm{V}}$$
##\boxed{R_{TH}}##
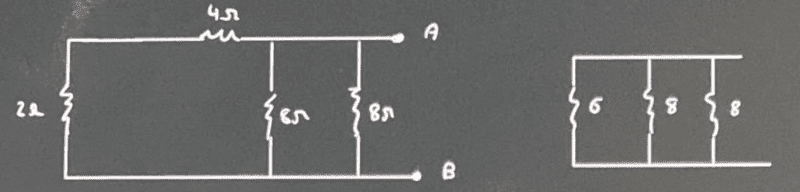
$$\dfrac{1}{R_{TH}}=\dfrac16+\dfrac18+\dfrac18 \rightarrow \boxed{R_{TH}=2,4\, \Omega}$$
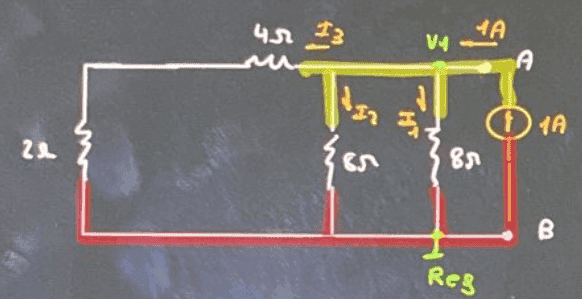
$$V_1\rightarrow -1+I_1+I_2+I_3=0\rightarrow$$
$$\rightarrow 1=\dfrac{V_1}{8}+\dfrac{V_1}{8}+\dfrac{V_1}{6}\rightarrow$$
$$\rightarrow 12=3V_1+2V_1=5V_1\rightarrow$$
$$\boxed{V_1=\dfrac{12}{5}=2,4\, \Omega}$$
$$V_1=R_{TH}\rightarrow \boxed{R_{TH}=2,4\, \Omega}$$
##\boxed{I_N}##
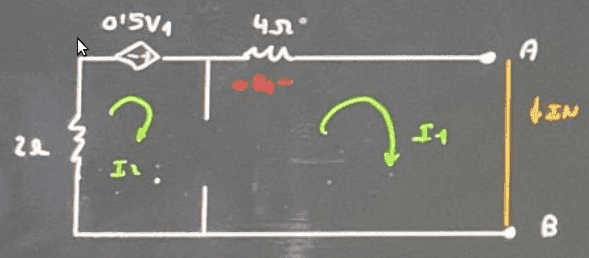
$$R_{TH}=\dfrac{V_{TH}}{I_N}=2\, \Omega \rightarrow \boxed{R_{TH}=2\, \Omega}$$
I was doing this exercise and the time to calculate the intensity and the Norton resistance doesn't add up... I've done it in different ways and I don't know where I fail. I don't know which one is right.
My attempt at a solution:
a) ##\boxed{V_{TH}}##
- Current source equations ##\rightarrow \boxed{2=I_2-I_1}##
- Control variable equations ##\rightarrow V_1=4I_2\rightarrow \boxed{0=4I_2-V_1}##
- Super Mesh ##\rightarrow -0,5V_1+2I_1+I_2(4+8)-8I_3=0\rghtarrow \boxed{0=2I_1+12I_2-8I_3-0,5V_1}##
- Mesh 3 ##\rightarrow 16I_3-8I_2=0\rightarrow \boxed{-8I_2+16I_3=0}##
We know that ##\rightarrow V_B=V_{TH}##
$$V_A=0+1,5\cdot 2=3\, \textrm{V}$$
$$V_B=V_A+1-0,5\cdot 4=2\, \textrm{V}$$
$$\boxed{V_{TH}=2\, \textrm{V}}$$
##\boxed{R_{TH}}##
$$\dfrac{1}{R_{TH}}=\dfrac16+\dfrac18+\dfrac18 \rightarrow \boxed{R_{TH}=2,4\, \Omega}$$
$$V_1\rightarrow -1+I_1+I_2+I_3=0\rightarrow$$
$$\rightarrow 1=\dfrac{V_1}{8}+\dfrac{V_1}{8}+\dfrac{V_1}{6}\rightarrow$$
$$\rightarrow 12=3V_1+2V_1=5V_1\rightarrow$$
$$\boxed{V_1=\dfrac{12}{5}=2,4\, \Omega}$$
$$V_1=R_{TH}\rightarrow \boxed{R_{TH}=2,4\, \Omega}$$
##\boxed{I_N}##
- Current equations: ##\boxed{2=I_N-I_2}##
- ##S\rightarrow \boxed{4I_N+2I_2-0,5V_1=0}##
- ##V_1=4I_1\rightarrow \boxed{0=4I_N-V_1}##
$$R_{TH}=\dfrac{V_{TH}}{I_N}=2\, \Omega \rightarrow \boxed{R_{TH}=2\, \Omega}$$
I was doing this exercise and the time to calculate the intensity and the Norton resistance doesn't add up... I've done it in different ways and I don't know where I fail. I don't know which one is right.