cnh1995
Homework Helper
Gold Member
- 3,487
- 1,165
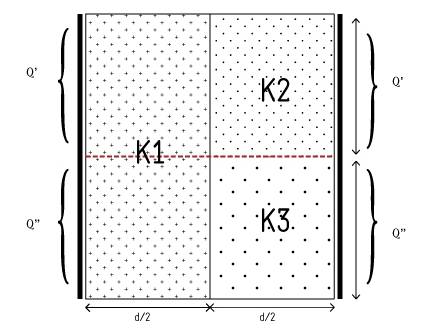
Ok. But the middle pair looks shorter than the other two. You need to put the plates at the boundaries of the dielectrics in order to distinguish the three capacitors.gracy said:No , there are only 4 plates in total.