To calculate the forces on a composite body

[gnits]

Homework Statement

To calculate forces on a composite body

Relevant Equations

Moments and Force Balancing

Can I please ask for help regarding the following:

A uniform rod AB of length 3L is freely hinged to level ground at A. The rod rests inclined at and angle of 30 degrees to the ground resting against a uniform solid cube of edge L. Contact between the rod and the cube is smooth and contact between the cube and the ground is rough. Find the reaction between the rod and the cube and the coefficient of friction between the cube and the ground if the cube is on the point of slipping. The weight of the cube is twice the weight of the rod.

Here's a diagram (u = coefficient of friction) :

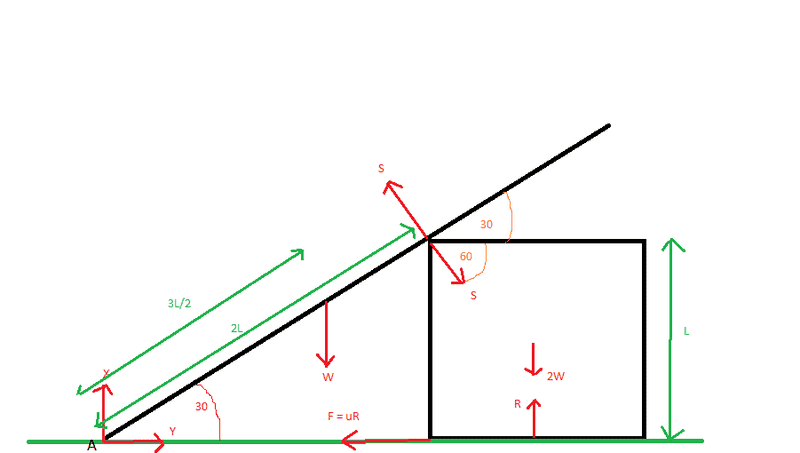
I have actually correctly answered the question, obtaining the same anwers as given in the textbook of:

s = 3 * sqrt(3) * W / 8

and

u = 3 * sqrt(3) / 41

(also as part of the calculation I have that R = 41 * W / 16 )

I did the above by first considering the rod alone and taking moments about A, and then by considering the cube alone and resolving horizontally and vertically. All worked fine and I agree with the textbook answers.

My question is that, if I consider the system as a whole and take moments about A I get:

(3*L/2) * (sqrt(3)*W / 2) + 2 * W * (sqrt(3)*L + L/2) - R*(sqrt(3) * L + L/2) = 0

and this does not lead to R = 41 * W / 16.

Have I formed the equation wrongly? Is considering the whole body like this valid?

Thanks,
Mitch.

 

[BvU]

Hi,

and this does not lead to R = 41 * W / 16.

Intriguing, isn't it ?

Could it be that the line of action of force R does not concide with that of force 2W ?

$\$

 

[gnits]

Hi,Intriguing, isn't it ?

Could it be that the line of action of force R does not concide with that of force 2W ?

$\$

Thanks, I see now. The line of action of R in this situation is not known a priori.