Total force that a fluid exerts on a cylinder

[Guillem_dlc]

Homework Statement

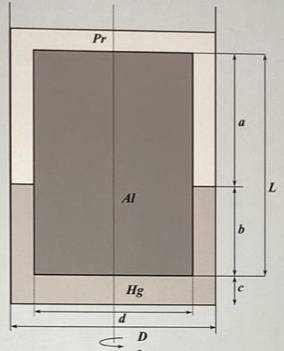
A cylinder of diameter $d=12,0\, \textrm{cm}$ and height $L=1,1\, \textrm{m}$ is immersed floating at the interface between mercury ($\rho_{hg}=13580,0\, \textrm{kg}/\textrm{m}^3$ and $\mu_{hg}=0,0015\, \textrm{Pa}\cdot \textrm{s}$) and liquid paraffin ($\rho_{pr}=850,0\, \textrm{kg}/\textrm{m}^3$ and $\mu_{pr}=0,2\, \textrm{Pa}\cdot \textrm{s}$) within a glass tube of diameter $D=12,2\, \textrm{cm}$. The cylinder is at $c=0,2\, \textrm{cm}$ from the bottom of the tube, the part immersed in mercury has a length of $b=40,0\, \textrm{cm}$ and the part immersed in liquid paraffin has a length of $70,0\, \textrm{cm}$, as shown in the figure.

The cylinder is rotated by $100,0 \, \textrm{rpm}$. Neglecting the friction at the base of the cylinder and the tube, determine the total force, in absolute value, that the fluid exerts on the cylinder, at $\textrm{N}$.

Relevant Equations

$F=\tau A$

Figure:

I have calculated the density of the cylinder: $5479,0\, \textrm{kg}/\textrm{m}^3$.

Attempt at a Solution:
$$d=0,12,\,\, L=1,1,\,\, D=0,122,\,\, e=0,002,\,\, c=0,02,\,\, b=0,4,\,\, a=0,7$$
$$\omega =100\, \textrm{rpm}=10,472\, \textrm{rad}/\textrm{s}\quad e=0,122-0,12=0,002$$
We know that: $F=\tau A=\mu \dfrac{\omega r}{e}\cdot A\rightarrow$
We have two $\mu$'s and two different areas:

• Hg $\rightarrow A=\pi r^2+2\pi r\cdot b$
• Pr $\rightarrow A=\pi r^2+2\pi ra$

$$\rightarrow F=\dfrac{\omega r}{e}(\pi r^2+2\pi rb+\pi r^2+2\pi ra)(\mu_{Hg}+\mu_{Pr})=$$
$$=\dfrac{\omega r}{e}(2\pi r^2+2\pi r(b+a))(\mu_{Hg}+\mu_{Pr})=\dfrac{\omega 2\pi r^2}{e}(1+b+a)(\mu_{Hg}+\mu_{Pr})$$
$$=50,11\, \textrm{N}$$
Here I don't know when I should use the integral and when I shouldn't. Would you do it like this?

 

[Guillem_dlc]

I've already got this one! Thanks

 

[haruspex]

It says to neglect the friction at the base. If you don't neglect it, you have to consider that the velocity gradient varies across it.
Doesn't seem right that it asks for the total force. The total force would be the buoyancy. What you have calculated appears to be a torque. Maybe it’s the translation.