guyvsdcsniper
- 264
- 37
- Homework Statement
- Let A=(x1,y1) and B=(x2,y2) be two points near and on the same side of a positively charged sheet with a uniform surface charge density. The electric field E⃗ due to such a charged sheet has the same magnitude everywhere and points away from the sheet, as shown in
- Relevant Equations
- V= -E*ds
So I know that E = -ΔV/Δs. If I wanted to solve for change in potential I could rearrange this equation and get Δ = -E*ds. With that information I believe I can solve the problem below. But in both solutions provided below, the negative sign goes away. Now I know I can pull the E out because it is uniform. Mylab does not go into detail on why the negative goes away. The hand written work includes the negative up until the 2nd to last step and I don't see how they got rid of it.
Any help with why the negative goes away?
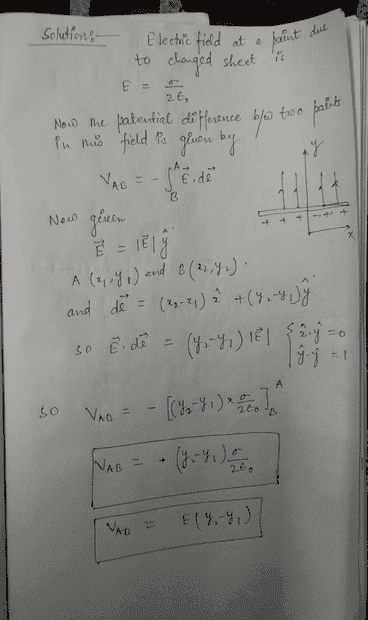

Any help with why the negative goes away?