Uncertainty in an experiment with an image viewed through a big slit

[dom_quixote]

This is a simple experiment that demonstrates how it is possible to draw conclusions similar to those of quantum physics, without having to "invade" the microscopic world.

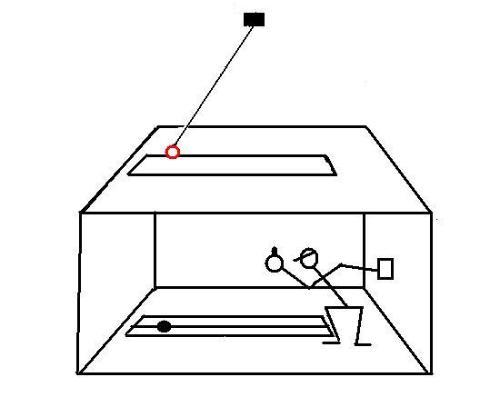
A student is led into a windowless room, which has only a slit in the ceiling.

The light that passes through the slit is composed of parallel rays and illuminates ortogonally a metric scale inscribed on the floor of the room.

Two devices are installed on the ceiling of the room.

In the first test, a pendulum is installed over the slit:

Note:
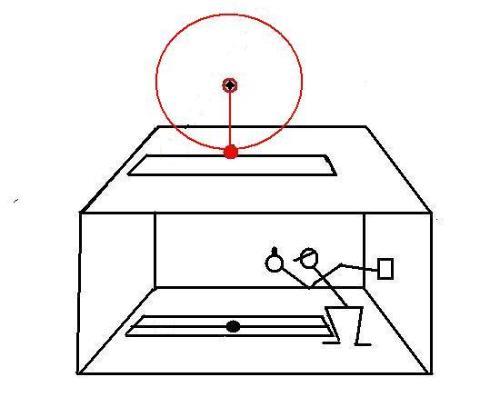
The pendulum is constantly driven to compensate for frictional energy loss.In the second test, a device that rotates at constant angular speed is installed over the slit:

The spheres that are attached to both devices are the same size and same mass.

The student has a stopwatch, pencil and notebook.

With these resources in hand, the student can draw some conclusions about the shadow projected on the floor of the room.

1 - When the shadow is at the extremes of the scale, he will be able to say that the speed of the sphere is zero, as long as the object is stuck in a pendulum. If the sphere is attached to the rotating device, the speed of the sphere will always be at maximum speed

2 - When the shadow is in the center of the scale, the speed of the shadow is maximum, but the student has no way of determining the position of the sphere. If the sphere is attached to a pendulum, it will be close to the ceiling of the room. If the sphere is attached to the rotating device, it can be close together in one of two different places.

Of course, the shadow's focus varies with the sphere's distance from the floor. But this variation is small and can go unnoticed.

The summary of student work will be:

"It's not possible to determine the velocity and the position of the body that casts the shadow on the floor at the same time. When you know the velocity, you don't know the position. When you know the position, you don't know the velocity."

One last question:

Is the pendulum's shadow velocity exactly equal to the constant angular velocity device's shadow?

 

[PeroK]

As you are using classical concepts to describe that experiment, there is no significant uncertainty in the sense of quantum uncertainty. Everything has well-defined position and momentum at all times, according to its classical trajectory.

The only uncertainties are experimental.

 

[kuruman]

This thought experiment fails in my opinion as an analogy. For a mass $m$ undergoing circular motion, the mathematical description of its position in the xy-plane is given by $$\vec r=R\cos\omega t~\hat x+R\sin\omega t~\hat y$$If you look down the z-axis, you will see the mass describing a circle in the xy-plane. However, if you look down the y-axis and see the xy-plane edge on, you will not see any displacement in the y-direction. In that case, the equation describing the motion would be $$\vec r=R\cos\omega t~\hat x$$which is indistinguishable from the one-dimensional motion of a mass at the end of a spring with constant $k=m\omega^2$. It is true that simply by observing the motion of the orbiting mass edge on is not enough to determine whether it is closer or farther from you but that is not a result of the uncertainty principle; it is a result of lack of information.

I think saying that the UP is about not knowing both the position and momentum of a particle exactly is an oversimplification that omits the context. The UP is a direct result of the wave description of particles. Think of it as two extremes. The first extreme is a pure monochromatic wave describing the particle that extends from $-\infty$ to $+\infty$. You can measure the wavelength $\lambda$ as the peak-to-peak separation anywhere in that interval and you will get the same number, i.e. you know the wavelength exactly. Using de Broglie relation $\lambda=h/p$, it follows that you know the momentum exactly.

But where is the particle?

It could be anywhere in the interval from $-\infty$ to $+\infty$ because everything looks the same. You might say, "well, I know that I can form localized packets by adding waves of different wavelengths". The more wavelengths you add, the more localized the packet and you can say that the particle is within an interval $\Delta x$. The price you pay for that is that the momentum becomes fuzzier because it is a superposition of many wavelengths. All you can say is that the momentum is within an interval $\Delta p$. If you add infinitely many wavelengths, you get to the other extreme and have a particle that is localized to a point which means that its position is exact.

But what do you put in the de Broglie relation to find its momentum?

 

[dom_quixote]

I think saying that the UP is about not knowing both the position and momentum of a particle exactly is an oversimplification that omits the context.

I agree with you, Kuruman. But this is how the effect is presented to the lay public, which includes myself.

When I intuited this experiment, I wanted to demonstrate the difficulty of understanding a phenomenon before theorizing it.

I can imagine the difficulty of "observing" a quantum phenomenon, and then theorizing it.