- #36
jaumzaum
- 434
- 33
ghwellsjr said:No, your brother will not receive many messages from you at the moment of his about-face. His about-face will not cause him to receive any messages from you. What's going to happen is that for the first half of his trip, he will receive messages from you at a slower rate than he sends them (1/R as I said in my first post to you), then for the second half of his trip he will receive messages from you at a faster rate than he sends them (R).
So for your example of your brother traveling at 0.5c, we can use the Relativistic Doppler formula to calculate what R is:
√((1+β)/(1-β)) = √((1+0.5)/(1-0.5)) = √((1.5)/(0.5)) = √3 = 1.732
And 1/R is the reciprocal, 0.57735.
This means that he will see your yearly messages coming to him slower than his during the first half of the trip. In fact it will take 1.732 years before he sees your first message.
And for the last half his trip, he will see your messages arriving more often than once per year according to his clock. It will only take 0.57735 years between each of your messages.
Now without knowing how long the trip will take, we can average these two numbers:
(1.732+0.57735)/2 = 2.30935/2 = 1.154675
This is the final ratio of your two clocks when he returns. How ever many years it took him according to his clock, yours will be 1.154675 times that amount.
So let's say your brother travels away at 0.5c for 13 years and then takes 13 years to get back at the same speed. Here is a spacetime diagram to show what is happening according to your rest frame. I show you as a thick blue stationary line with dots every year and your messages going out as thin blue lines traveling at c. I show your brother as a thick black line traveling at 0.5c with black dots every year and his messages coming back to you as thin black lines:
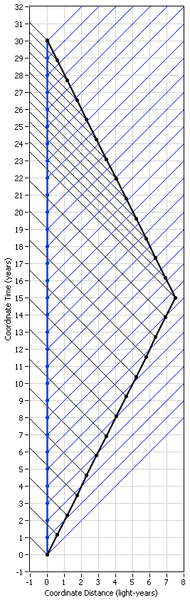
Now let's see how the previous calculations based on Relativistic Doppler fit in with this diagram. First off, I said that the rate at which your brother receives your yearly messages take 1.732 of his years. Can you see that on the graph? For example, at about his year 12, just before he turns around, he is just receiving the message you sent at your year 7. Can you follow that? If we divide 12 by 7 we get 1.714 which is about right. (We don't expect it to be exact because he didn't receive your message exactly at his year 12.)
Furthermore, if you look at your year 12, you can see that you are just receiving his message from year 7. It's symmetrical.
Now you should be able to see that after he turns around, he starts receiving your messages faster than one per year. In fact, from about his year 19 (you'll have to count his dots) to when you meet at his year 26, he will have received your messages from year 18 to 30. That is a ratio of the differences of (26-19)/(30-18) = 7/12 = 0.583, close enough to 0.577.
And in a similar manner, you can see that from his year 14 (just after he turns around) until you meet (12 years of messages from him), you will see them from your year 23 to your year 30 (7 years) and the reciprocal ratio applies.
Now that we can look at a spacetime diagram, we can see that the reason why the two of you age differently is because your brother sees these two ratios for half of his total trip time each but you see the smaller ratio for three-quarters of the time and the higher ratio for just one-quarter of the time. This means you are seeing him age less for a longer time while he sees you age less for half the time.
The last thing we want to notice is that ratio of your final age difference is 30/26 or 1.1538, very close to the actual 1.154675. (Again, these numbers are not exact because we're eyeballing them off the diagram.) This ratio is the famous value of gamma which is also the time dilation factor which shows in the diagram as the ratio of the coordinate time for your brother compared to his actual time on his clock. Can you see that?
Now I want to show you what the exact same information presented in the first diagram looks like in two more diagrams based on the IRF's in which your brother is at rest, first during his outbound leg and then during his inbound leg. First the outbound leg:
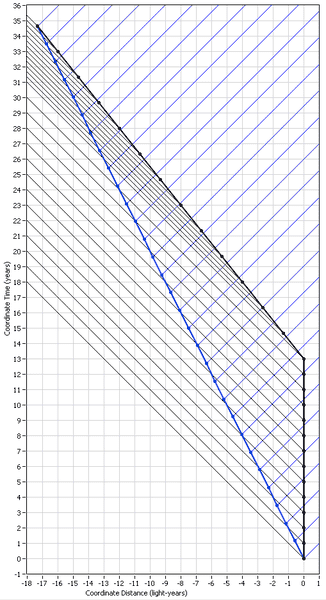
Notice how your brother's time is not dilated during the outbound leg (because he is at rest) but yours is. Note also that he has to travel at a higher speed than 0.5c (look up "veloctiy addition" in wikipedia to see that this higher speed is 0.8c) when he turns around and therefore now has more time dilation than you have. Nevertheless, all the signals between the two of you continue to travel at c and arrive at exactly the same times according to your own clocks as they did before. Does this all make sense to you?
Finally the diagram for the IRF in which your brother is at rest during the inbound leg:
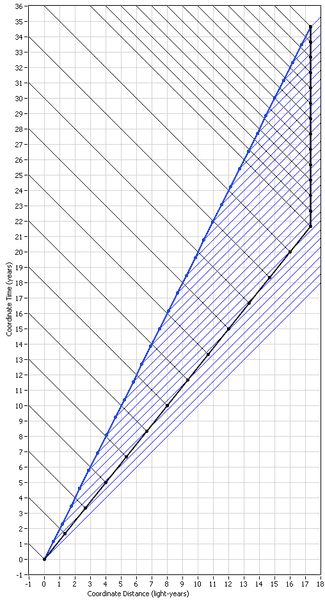
This is very similar to the previous diagram so I won't go into any more explanation except that I want to point out that when your brother turns around, in no case does that have any bearing on what you see, until some time later and even then, each diagram shows accurately what you actually see and what your brother actually sees during the entire scenario.
Any questions?
Thanks George! I mean, I really want to thank you, in all of the threads I've already posted here, I've never seen such a good and detailed answer as yours. I'm new in special relativity and you explained everything so carefully I could understood almost completely. I thought I had understood before, but I didn't know the explanation had nothing to do to what I suppose it was correct. There should be more guys like you here in PF. I want to thank everyone who answered this thread but the george's answer was phenomenal (at least for me). Now I think I'm startin g to understand special relativity.
And yes, I do have some questons, I would appreciate if you could help me again
How it would be the diagram if we take the referential frame as the whole trip of my brother (I mean, my brother is at rest in the whole time). I'm not being able to "close" the graphic. If my brother is a straight line, my lines can't be together as they are smaller than his. Is this right?