Uniformly accelerating frame of reference

[sweet springs]

To me at rest is having zero velocity. At rest or not depends on which FR you take. I am afraid it is different from your "things being at rest"

Please take a look at a drawing to express the situation I take.
.

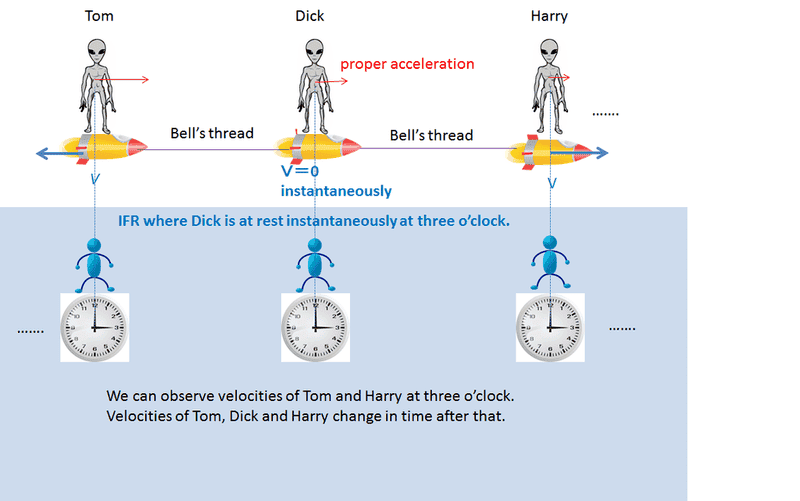
Dick keeps at rest in the uniformly acceleration system. Dick is at rest instantaneously in the IFR. Do they contradict?
Any teaching is appreciable. I still wonder Tom and Harry are also at rest instantaneously or not. I try math you suggested.
Thanks.

 

[sweet springs]

Thanks for good discussions. Let me deepen my understanding.The wrong answer a. seems to turn out to be right in another case that the ships are arranged to represent lattices of uniformly accelerating frame of reference. i.e.,

In an inertial frame of reference(IFR) let numerous standard space ships that load synchronized standard clocks place on all the space lattice, labelled with the coordinates.
Simultaneously the ships start to move to the same direction with constant proper acceleration. Proper accerelation of ships are arranged so that ships on a traverse line have same proper acceleration and nearby traverse lines keep constant distance.

a. There always is an instataneous IFR where all the ships are at rest.
b. In the instataneous IFR the distances between the ships in that direcion are constant.
c. In the instataneous IFR the clocks are not syncronized in that direction. Faster forward, delayed backward.
d. Let the ships have come to the initial fire state by having kept accerelation of the same manner at past. In the instantaneous IFR, distance of the ships in that direction were constant.

Rindler coordinate is interpreted as continuous get off and on the instantaneous IFRs.

Now I check math and I was right.

 

[sweet springs]

We seem to be going around in circles. Let's try this.
This much I can vouch for. I can't vouch for any remarks about "things being at rest" without some precise defintions of what is meant by "at rest", it's just too vague without a mathematical statement (of very rigorous non-mathematical one) as to exactly what you mean.

I will try to explain two possible meaning of "at rest".

In instataneous IFR, one ship has no velocity at the instant. Other ships would have velocities of non zero. Acceleration does not matter.

In proper frame of reference, or comoving frame of reference, all the ships keep zero velocity and zero acceleration. Metric of the frame would be function of time-space coordinates thus it could not be an IFR.

I take the former one. The latter might be of your concern.

 

[pervect]

I will try to explain two possible meaning of "at rest".

In instataneous IFR, one ship has no velocity at the instant. Other ships would have velocities of non zero. Acceleration does not matter.

In proper frame of reference, or comoving frame of reference, all the ships keep zero velocity and zero acceleration. Metric of the frame would be function of time-space coordinates thus it could not be an IFR.

I take the former one. The latter might be of your concern.

I think I agree that in the first sense, the velocities are zero, but I took some shortcuts in the analysis.Using only 2 dimensions in Rindler coordinates, t,x, with $ds^2 = -(1+gx)^2 dt^2 + dx^2$ the 4-velocity of a ship with a constant Rindler coordinate x is $\partial t/\partial \tau = 1/(gx+1)$, $\partial x / \partial \tau = 0$

In Minkowskii coordinates of the true globallyi inertial frame, the 4-velocity the 4-velocity using the transforms from post #35 is
$\partial T / \partial \tau = (dT/dt) (dt/d\tau) = [(gx+1) \cosh gt] [1/(gx+1)] = \cosh gt$, $\partial X / \partial \tau = (dX/dt) (dt/d\tau) = \sinh gt$

So the 3-velocity $dX/dT$ is $tanh gt$. Using the equations from post #35 (the second set with the origin offset) this is just $dX/dT = T/(X+1/g)$.

So it's obvious that at T=0, all the velocities are zero. It's not particularly obvious what happens when we do a Lorentz boost to a co-moving frame at some time T that is nonzero, but here is where I take a shortcut. There isn't anything particularly special about T=0, so the velocities should be zero in the comoving frame, though the calculations would be rather tedious.

 

[PeterDonis]

There isn't anything particularly special about T=0

There isn't for the Rindler congruence (the set of worldlines in which the proper acceleration varies as 1 / x), but there is for the Bell congruence (the set of worldlines in which the proper acceleration is the same on every worldline); in the latter case, $T = 0$ in the global inertial frame is the only spacelike hypersurface in which all of the worldlines in the congruence are simultaneously at rest.

It looks like both congruences are being discussed in this thread; it might help to be very clear about which one is being talked about.

 

[sweet springs]

There isn't for the Rindler congruence (the set of worldlines in which the proper acceleration varies as 1 / x), but there is for the Bell congruence (the set of worldlines in which the proper acceleration is the same on every worldline); in the latter case, $T = 0$ in the global inertial frame is the only spacelike hypersurface in which all of the worldlines in the congruence are simultaneously at rest.

It looks like both congruences are being discussed in this thread; it might help to be very clear about which one is being talked about.

Thanks. I thought about the Rindlere congruence with rockets are tighten with threads. In the Rindler congruence threads are tight but not torn apart that is usulally reffered in Bell's congruence. It might have been a misconfusing saying.

 

[pervect]

There isn't for the Rindler congruence (the set of worldlines in which the proper acceleration varies as 1 / x), but there is for the Bell congruence (the set of worldlines in which the proper acceleration is the same on every worldline); in the latter case, $T = 0$ in the global inertial frame is the only spacelike hypersurface in which all of the worldlines in the congruence are simultaneously at rest.

It looks like both congruences are being discussed in this thread; it might help to be very clear about which one is being talked about.

Yes - my remarks and calculations were specific to the Rindler congruence. It would be better (but more work) not to take shortcuts (as I did) which might not apply in other circumstances. It's probably worth noting that the Bell congruence, the sliding block congruence and a rotating congruence would all likely NOT satisfy the "at rest" criterion from the viewpoint of an ICMIRF centered around one specific reference observer.

 

[PeterDonis]

It's probably worth noting that the Bell congruence, the sliding block congruence and a rotating congruence would all likely NOT satisfy the "at rest" criterion from the viewpoint of an ICMIRF centered around one specific reference observer.

Yes, I think this is correct. But it's also worth noting that the reason for this is different in the case of the Bell congruence, compared to the other two. The Bell congruence has nonzero expansion (but zero shear and vorticity); the other two have nonzero vorticity (but zero expansion and shear).