jangheej
- 16
- 0
I have a question about force needed to peel a tape.
1. If an external force does work on a tape, to what kind of energy is it transformed?
There must be some kind of energy stored in the tape, but I can't think of any.
some papers mention "strain energy", but I don't grasp the concept of it.
2. Where does the adhesive force come from? Is it from Van der waals force?
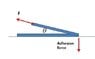
3. I drew the forces in the attached file, and accordingly, since the vertical component of the external force increases as the theta increases, it must be easier to peel the tape off the surface when the angle increases. But theories and simple experiments show the opposite result. What is wrong with the picture?
1. If an external force does work on a tape, to what kind of energy is it transformed?
There must be some kind of energy stored in the tape, but I can't think of any.
some papers mention "strain energy", but I don't grasp the concept of it.
2. Where does the adhesive force come from? Is it from Van der waals force?
3. I drew the forces in the attached file, and accordingly, since the vertical component of the external force increases as the theta increases, it must be easier to peel the tape off the surface when the angle increases. But theories and simple experiments show the opposite result. What is wrong with the picture?