What if the Bohmian model turned out to be correct?

[akhmeteli]

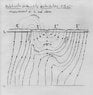
1. We cannot discuss it without drawings. Therefore, please see the picture in my
http://xxx.lanl.gov/abs/quant-ph/0208185 [Found.Phys.Lett. 17 (2004) 363].
Is it 1 particle or 3 particles?

I would say there are 3 particles, although you can say that it is 1 particle (along the lines of the Wheeler's idea), and I could agree. As you said, it's pretty much the same. However, I tend to believe that even if the first particle disappears, the other two will be real, although they may annihilate later.

2. The particle trajectories are not solutions of the wave equations. Perhaps you meant something else?

No, that's what I meant. You see, the Bohmian trajectory can be built on the basis of a wavefunction (which is a solution of a wave equation), as a current line. The current for such solutions is conserved, so there are no sources and no sinks. I see no reasons for instantaneous disappearance of the two remaining particles.

3. You missed the point. The dotted part is unphysical because this part is actually NOT a solution of the particle-trajectory equation of motion. This is because the interaction with the measuring apparatus changes the wave function. (Sorry, but I must suspect again that you are not familiar with the measurement theory in Bohmian mechanics. Please inform me, by PM if you want, if this is the case. It is essential for the efficiency of further discussion.)

I already admitted that I had mixed up the dotted part of the trajectory (related to the future) with the dashed one (related to the past), and I apologized. I could agree that the dotted part is unphysical.

I still don't know how this is relevant, but I am familiar with the measurement theory in Bohmian mechanics, though I am not sure my knowledge is very profound.

Now the dashed part is unphysical because it is no longer joined with the solid part, so it is NOT a part of the same trajectory.

It may not be a part of the same trajectory, but the particles that the dashed part describes are real, if you ask me, not unphysical. You state that this part is unphysical. I fail to see convincing arguments in favor of such statement.

4. Can you give me an appropriate reference in which this was shown? I've seen books with similar statements, but such claims were based on hand waving, not on serious calculations based on principles of quantum field theory.

There may be different opinions on whether it was appropriately "shown", but the article is Zs. Phys., 69, 56, 1931 (I guess there is an English translation somewhere, allegedly, in Wheeler, J. A., and W. H. Zurek, eds., 1983, Quantum Theory and Measurement, (Princeton University Press, Princeton, NJ). ) They don't mention pair production (for obvious reasons:-), it is mentioned in Berestetskii, V. B., Lif****z, E. M., & Pitaevskii, L. P. 1982, Quantum Electrodynamics (Oxford:
Pergamon).

 

[akhmeteli]

But the experimental status of Bohmian mechanics is also problematic. So how arguments based on BM can convince you?

First, I would say the experimental status of the Bohmian mechanics is better than that of the string theory, as its predictions coincide with those of quantum mechanics, at least in the nonrelativistic case (one may say that the same is true for the string theory with certain values of parameters, but there are many more additional radical assumptions in the string theory than in the Bohmian mechanics.). Second, we both use arguments based on QFT, and they seem much more reliable to me, as QFT is properly tested. So I don't think I just refuse to accept anything as a starting point, but I cannot accept everything in this capacity.

 

[Demystifier]

It may not be a part of the same trajectory, but the particles that the dashed part describes are real, if you ask me, not unphysical. You state that this part is unphysical. I fail to see convincing arguments in favor of such statement.

I think I see now where is the source of misunderstanding between you and me. Not really disagreement, but misunderstanding of each other (at least I hope so). So let me explain the things more carefully.

Consider first a nonrelativistic 1-coordinate wave function. All Bohmian trajectories are potentially physical. However, in a single physical case, only one is actually physical. A priori you cannot know which one, but you know that there is one of them that is actually realized. That's what nonrelativistic Bohmian interpretation says. Do you agree?

Now the generalization to a relativistic 1-coordinate wave function. Again, all Bohmian trajectories are potentially physical, including the dashed ones. However, only one connected trajectory is actually physical. For example, if a dashed trajectory is actually physical, then no solid trajectory is actually physical. Conversely, if a solid trajectory is actually physical, then no dashed trajectory is actually physical. Do you still agree?

Now the main point. IF you know with certainty that particle were present somewhere at Sigma_0, THEN you know with certainty that the actually physical trajectory is one of the solid ones. Therefore, you know that the actually physical trajectory is not a dashed one.

Do you agree with such a sharpened explanation?

 

[akhmeteli]

Finally, what IF the experiment turn out to agree with this prediction? Then we have an experimental proof that both BM and string theory are correct.

What bothers me is: what IF the results of the experiment disagree with this prediction? Whose fault would that be? BM's? String theory's? Or maybe both will be falsified? I am afraid you are pushing both the one-particle quantum mechanics and the one-particle Bohmian mechanics to the limit where they are known to fail or will probably fail due to pair production. When you try to compare them in the domain they are not supposed to describe correctly, even potential disagreement with experimental results may be not very meaningful, because we know the natural factor that can cause it.

 

[Demystifier]

First, I would say the experimental status of the Bohmian mechanics is better than that of the string theory, as its predictions coincide with those of quantum mechanics, at least in the nonrelativistic case (one may say that the same is true for the string theory with certain values of parameters, but there are many more additional radical assumptions in the string theory than in the Bohmian mechanics.). Second, we both use arguments based on QFT, and they seem much more reliable to me, as QFT is properly tested. So I don't think I just refuse to accept anything as a starting point, but I cannot accept everything in this capacity.

I see. But let me explain my way of thinking (for which I do not claim that it is better then other ways of thinking). The main reason I like BM is NOT because its predictions are consistent with observations (although they are, but so are the predictions of other interpretations), but because I find BM very elegant. Many scientists will say that "elegance" is irrelevant, but for me (and certainly not only me) it is very relevant.

Now, if you want to make BM consistent with particle creation and quantum field theory (QFT), it is possible to do that, but NOT in an elegant way. But I insist on elegance, that's my guiding principle in search for a more fundamental theory. What I find is that, if QFT is replaced by strings, or more precisely, if QFT is viewed as only an effective theory that emerges from fundamental strings, then the elegance of BM is recovered. For me, it is a good hint that the string version of BM could be the right theory.

Even if this is not your way of thinking (which is understandable), I hope you understand now why I think the way I do.

 

[Demystifier]

What bothers me is: what IF the results of the experiment disagree with this prediction? Whose fault would that be? BM's? String theory's? Or maybe both will be falsified?

What would be falsified is a single elegant theory that unifies BM and string theory. Neither BM nor string theory per se would be falsified because different (for me less elegant) versions of BM and string theory are also possible.

 

[akhmeteli]

Consider first a nonrelativistic 1-coordinate wave function. All Bohmian trajectories are potentially physical. However, in a single physical case, only one is actually physical. A priori you cannot know which one, but you know that there is one of them that is actually realized. That's what nonrelativistic Bohmian interpretation says. Do you agree?

I agree that this is what nonrelativistic Bohmian interpretation says.

Now the generalization to a relativistic 1-coordinate wave function. Again, all Bohmian trajectories are potentially physical, including the dashed ones. However, only one connected trajectory is actually physical. For example, if a dashed trajectory is actually physical, then no solid trajectory is actually physical. Conversely, if a solid trajectory is actually physical, then no dashed trajectory is actually physical. Do you still agree?

No. I believe both the solid and the dashed trajectories are physical at Sigma.

No the main point. IF you know with certainty that particle were present somewhere at Sigma_0, THEN you know with certainty that the actually physical trajectory is one of the solid ones. Therefore, you know that the actually physical trajectory is not a dashed one.

Do you agree with such a sharpened explanation?

No. For example, if there is no measurement, and the solid trajectory is physical, then the dashed trajectory is also physical, otherwise there is a sink. If there is a measurement, that does not make the dashed trajectory unphysical. Yes, it means that there are more than one particle. Yes, it means that one-particle theories are not entirely sufficient in this case. This is how I see it. Apparently, you disagree, and maybe you're right, and I am wrong. But so far I don't see convincing arguments that could make me change my position.

 

[Demystifier]

No. I believe both the solid and the dashed trajectories are physical at Sigma.

But for a given solid trajectory, how will you determine WHICH dashed trajectory is the physical one? Since the dotted part is no longer physical (we agree on that), the solid and dashed curves are not two parts of one connected curve, so for a given solid trajectory, the dashed trajectory is not unique. Do you agree?

Now, if you allow that more than one trajectories are physical, how you will determine how many of them are physical? For example, can TWO almost parallel dashed trajectories by physical? If not, why?

 

[Demystifier]

Here I attach I picture that should make more clear what I am talking about.

 

[akhmeteli]

I see. But let me explain my way of thinking (for which I do not claim that it is better then other ways of thinking). The main reason I like BM is NOT because its predictions are consistent with observations (although they are, but so are the predictions of other interpretations), but because I find BM very elegant. Many scientists will say that "elegance" is irrelevant, but for me (and certainly not only me) it is very relevant.

Now, if you want to make BM consistent with particle creation and quantum field theory (QFT), it is possible to do that, but NOT in an elegant way. But I insist on elegance, that's my guiding principle in search for a more fundamental theory. What I find is that, if QFT is replaced by strings, or more precisely, if QFT is viewed as only an effective theory that emerges from fundamental strings, then the elegance of BM is recovered. For me, it is a good hint that the string version of BM could be the right theory.

Even if this is not your way of thinking (which is understandable), I hope you understand now why I think the way I do.

I share some of your beliefs, but I wish I could be more enthusiastic about such an approach. I am not in a position to assess mathematical beauty of the string theory, but from the physical point of view it seems like it may need a touch of the Occam's razor. Anyway, even if such approach is absolutely correct, that is not very encouraging, as it means that the problem of interpretation of quantum mechanics will not be solved until the string theory is confirmed experimentally, and that may take a couple of centuries... So I very much hope this is not the way Nature works:-) . Furthermore, I feel that BM, however elegant, is not elegant enough. The fact that the electromagnetic potential can replace the quantum potential as a guiding field for the Klein-Gordon-Maxwell system suggests that BM can be made much more elegant.

 

[Schrodinger's Dog]

I share some of your beliefs, but I wish I could be more enthusiastic about such an approach. I am not in a position to assess mathematical beauty of the string theory, but from the physical point of view it seems like it may need a touch of the Occam's razor.

No one is except string theorists. It's a fortified position where peer review comes only from within, which is another reason I deeply distrust the "theory", apart from the obvious one - it has no evidence at all.

I agree, there's no problem with creating imaginative elegant theories, provided they actual have some relation to the real world at some point.

I genuinely hope that most physicists are not in a position to discard any interpretation out of hand or completely, that would be very arrogant, given they are all flawed to some extent or incomplete. There's something about string theory, like MWI that sets my spidey sense a tingling though. I have to admit I am prejudiced.

 

[akhmeteli]

What would be falsified is a single elegant theory that unifies BM and string theory. Neither BM nor string theory per se would be falsified because different (for me less elegant) versions of BM and string theory are also possible.

That's what I mean. In general, BM does not predict those experimental differences, that is a prediction of your version of BM. Again, maybe you're absolutely right, but the mechanism that you suggest to prove that such differences exist does not seem very natural to me.

 

[akhmeteli]

But for a given solid trajectory, how will you determine WHICH dashed trajectory is the physical one? Since the dotted part is no longer physical (we agree on that), the solid and dashed curves are not two parts of one connected curve, so for a given solid trajectory, the dashed trajectory is not unique. Do you agree?

I'm afaid not. The wavefunction is also real, so the physical dashed trajectory is the dashed trajectory that is a continuation of the solid trajectory for that wavefunction.

Now, if you allow that more than one trajectories are physical, how you will determine how many of them are physical? For example, can TWO almost parallel dashed trajectories by physical? If not, why?

I explained above that there is a way to define the unique physical trajectory, so I don't need to answer this question. That does not mean that there cannot be some additional physical trajectories that are just not described by our one-particle theory (so those additional trajectories relate to some other particles).

However, I should point out that the above was written for the standard BI. On the other hand, the following two possibilities seem also feasible to me: 1). ALL trajectories possible for the wavefunction are physical (so actually we have an infinite number of particles). 2). No trajectories are physical (so there are no particles, just the electromagnetic field that they are supposed to interact with). But I guess this is speculative.

 

[Demystifier]

I'm afaid not. The wavefunction is also real, so the physical dashed trajectory is the dashed trajectory that is a continuation of the solid trajectory for that wavefunction.

My point is that there is NO continuation, simply because the doted part (that should interpolate between them) does not exist.

 

[Demystifier]

Anyway, even if such approach is absolutely correct, that is not very encouraging, as it means that the problem of interpretation of quantum mechanics will not be solved until the string theory is confirmed experimentally, and that may take a couple of centuries...

One of the nice properties of my theory is that it is not true. Namely, my theory predicts an effect of strings (or more precisely of a specific form of boson-fermion unification emerging from strings) that can be tested at LOW energies. A type of experiment that is supposed to test it is not of a CERN (big accelerator) type, but of a Zeilinger (foundations of QM) type.

 

[Demystifier]

No one is except string theorists.

There is a myth that string theory is so complicated that only true experts in string theory can understand why this theory seems so promising. Fortunately, there is an undergraduate textbook on string theory that shows that this myth is not true:
B. Zwiebach, A First Course in String Theory
This is a serious, not a popular book, but still every theoretical physicist can understand it.

 

[akhmeteli]

My point is that there is NO continuation, simply because the doted part (that should interpolate between them) does not exist.

There is no actual continuation because of the measurement. However, you know the wavefunction, so you can say which dashed trajectory would have been the continuation of the given solid trajectory if there had not been any measurement, and this dashed trajectory is physical. Of course, it does not matter whether you actually know the wavefunction, as the WV is real, and it defines the physical trajectory.

 

[Schrodinger's Dog]

There is a myth that string theory is so complicated that only true experts in string theory can understand why this theory seems so promising. Fortunately, there is an undergraduate textbook on string theory that shows that this myth is not true:
B. Zwiebach, A First Course in String Theory
This is a serious, not a popular book, but still every theoretical physicist can understand it.

Yeah but would it enable you to criticize a current paper on string theory. Because I being the good soldier I am understand the principals of string theory, but I'll be damned if I'm going to learn the maths based on that. I mean extra dimensions that are curled up which solve infinity problems, like screwing up a graph or a piece of paper until the vector fits the way you want it to. It sounds to me like wishful thinking, like what science would be if mathematicians ruled the universe. I'd love to be wrong about it, but you wouldn't catch me doing pure maths and pretending it was science. Not that I'm planning on doing anything post grad anyway.

I read a critique by someone who'd left string theory that completely tore it to shreds IMO. Since then I've been reticent to believe in fairies. I know that sounds quite arrogant, but I really don't like it, I never liked it, and when I understood it I liked it even less. I suppose I shouldn't I might end up being totally wrong, but that's a win/win situation I'm prepared to face.

 

[akhmeteli]

One of the nice properties of my theory is that it is not true. Namely, my theory predicts an effect of strings (or more precisely of a specific form of boson-fermion unification emerging from strings) that can be tested at LOW energies. A type of experiment that is supposed to test it is not of a CERN (big accelerator) type, but of a Zeilinger (foundations of QM) type.

I did not know that. I wish you luck then.

 

[Fra]

Yeah but would it enable you to criticize a current paper on string theory.

I kind of agree with you and IMO you can criticize something in at least two ways.

(1) Either you criticize a paper in it's own context, say relative to the string framework, ie. as a string theorist would criticize say a collegues paper I presume. A string theorist would I presume, accept the string framework and all baggage it's contains, including that carried over from QM foundations and field theory, and work from there.

(2) Or you can critizise the entire string framework or it's foundations or strategy, relative to your own preferred view, but that's a more generic critique to the methodology.

I personally find the string foundations speculative. Therefor I am not even motivated to spend time to come up with a type-1 critics, which would include getting more detailed updated with their internal logic.

I can still appreciate some associations to string-like objects in a particular continuum limit, but the concept of a fundamental objective string is really not something I personally could accept as a basis for further research. But everyone is free to play their cards the way they feel is best. Noone has the answers.

I'm unable to tell a string theorist that they should not waste their time on it, because I don't think they are. I'm sure they see potential. All I know that I fail to motivate myself to investing my personal time in it.

/Fredrik

 

[Schrodinger's Dog]

Well no branch of pure mathematics no matter how esoteric is ever a waste of time. Imaginary numbers took 400 years before they found a real world use. I'm not arrogant enough to suppose there will never be any evidence for string theory, but I am consistent enough to say that I place string theory on the same level as any other hypothesis, and weigh the pros and cons accordingly. Like any scientist if you don't like the hypothetical there's nothing from stopping you studying something else. The only problem I had with it is that it was soaking up too much funding from physics in what is still an area of pure mathematics. Although in some more reality based Universities, funding comes from maths departments, as it should. But that's by the by.

 

[Demystifier]

However, you know the wavefunction, so you can say which dashed trajectory would have been the continuation of the given solid trajectory if there had not been any measurement, and this dashed trajectory is physical.

Sorry, but this doesn't make sense to me. In this way you can obtain almost any result you want, because you can allways consider a situation in which the wavefunction was something else instead of what it really was. Measurement plays no special fundamental role in Bohmian mechanics. Measurement only corresponds to a certain type of entangled wavefunctions. On the other hand, your proposal tacitly assumes that there is a fundamental difference between situations with and without measurements, which, to put it mildly, contradicts the spirit of BM.

 

[Demystifier]

I did not know that. I wish you luck then.

Thanks!
I find it truly amazing that there is a possibility that evidence for strings could come from experiments that test foundations of QM at low energies.

 

[Fra]

Yes, if you are a mathematician at heart so to speak then you probably has a different way of seeing things, and the formalism has it's own value, even if it would prove to have little or no physical value. Perhaps those people could see "mathematical physics" as potential area to propagate in.

But I guess that's the funders problem to direct money in the right places to serve their purposes. It will become my problem when tax money is used for it. But to be honest I really don't know how much tax money goes to string theory and how much comes from other organisations and donors. And I don't feel inclined to invest my thinking in those political issues at a formal level either, that would waste more of my resources than a fraction of lost tax money would :)

/Fredrik

 

[akhmeteli]

Sorry, but this doesn't make sense to me. In this way you can obtain almost any result you want, because you can allways consider a situation in which the wavefunction was something else instead of what it really was.

Sorry, Demystifier, I just don't get it. Who wrote the phrase: "The system is described by the wave function \psi(x) on M, i.e., between Sigma_0 and Sigma", you or I? :-). You know this is a phrase from your article, not mine. That means that we cannot take an arbitrary wavefunction, so I cannot consider any wavefunction but this one. So the physical trajectory is also well defined, as the wavefunction satisfies the wave equation. So the physical dashed trajectory cannot be arbitrarily chosen. Or maybe I don't understand something very simple, then could you explain?

Measurement plays no special fundamental role in Bohmian mechanics. Measurement only corresponds to a certain type of entangled wavefunctions. On the other hand, your proposal tacitly assumes that there is a fundamental difference between situations with and without measurements, which, to put it mildly, contradicts the spirit of BM.

Again, I am somewhat at a loss. I am just trying to discuss your article exactly as it was written by you, not by me: "The dotted curves above Sigma indicate the particle trajectories that might be realized if there were no measurement of particle positions on Sigma, i.e., if the system were described by \psi(x) even above Sigma. If there were no measurement on Sigma, and if the initial position of the particle were the point A on Fig. 1, then the particle would cross Sigma at 3 points, i.e., at A′, C−, and C+. However, owing to the measurement of particle positions, the actual wave function above Sigma is of the form \psi(x, y), where y represents the degrees of freedom of the measuring apparatus." I just humbly follow you, saying that if there had not been any measurement on Sigma, the particle would have been described by \psi(x) everywhere. Then I add that we can use this wavefunction to decide which dashed trajectory is physical, as the measurement should not affect the past (at least that is what I think). I am no more saying "that there is a fundamental difference between situations with and without measurements" than you do, I just repeat after you that the measurement changes the wavefunction. Again, maybe I am missing something simple and important, so I am looking forward for your further input.

 

[Demystifier]

Sorry, Demystifier, I just don't get it. Who wrote the phrase: "The system is described by the wave function \psi(x) on M, i.e., between Sigma_0 and Sigma", you or I? :-). You know this is a phrase from your article, not mine. That means that we cannot take an arbitrary wavefunction, so I cannot consider any wavefunction but this one. So the physical trajectory is also well defined, as the wavefunction satisfies the wave equation. So the physical dashed trajectory cannot be arbitrarily chosen. Or maybe I don't understand something very simple, then could you explain?

Now I really cannot understand you. Yes, \psi(x) is the wave function on M. But it is not a wave function ABOVE M. Therefore, you cannot use \psi(x) above M. Therefore, you cannot use the dotted part of the trajectory. Therefore, you cannot know which dashed trajectory should be attributed to a given solid trajectory. Which step in this reasoning is not clear?

 

[Demystifier]

No, that's what I meant. You see, the Bohmian trajectory can be built on the basis of a wavefunction (which is a solution of a wave equation), as a current line. The current for such solutions is conserved, so there are no sources and no sinks. I see no reasons for instantaneous disappearance of the two remaining particles.

Now I think I understand your way of reasoning. You seem to think that there is a fundamental flow of time. But such a picture of time is inconsistent with superluminal motions because there are Lorentz frames in which superluminal motions appear as motions backwards in time. Therefore, the only way to make superluminal motions consistent with relativity is to adopt the BLOCK-time picture, in which time does not flow, but simply is, just like space. See e.g. my
http://arxiv.org/abs/gr-qc/0403121 [Found.Phys.Lett. 19 (2006) 259]

Now, to understand my way of thinking (which is generally known as the block-time or block-universe picture of spacetime), imagine that the picture I have given in #114 is not a trajectory in 1+1 dimensional spacetime, but a trajectory in 2 dimensional space (at a fixed time). Would you now agree that the dashed trajectory is unphysical? If yes, then just try to think that time is nothing but another space coordinate, only with a different sign of metric. Then everything, at least formally, should become clear to you.

What may remain is a conceptual (not formal) problem with an intuitive notion of the flow of time, but that's another type of problem. The paper mentioned above, together with some references, might help.

 

[akhmeteli]

Now I really cannot understand you. Yes, \psi(x) is the wave function on M. But it is not a wave function ABOVE M. Therefore, you cannot use \psi(x) above M. Therefore, you cannot use the dotted part of the trajectory. Therefore, you cannot know which dashed trajectory should be attributed to a given solid trajectory. Which step in this reasoning is not clear?

I believe I can "know which dashed trajectory should be attributed to a given solid trajectory." The procedure is as follows: as I know \psi(x) on M, I can compute it above M using the wave equation and use the computed dotted trajectory (although the measurement makes it unphysical, I still can compute it) to find the dashed trajectory corresponding to the physical solid trajectory. So why cannot I "use \psi(x) above M"? I certainly can use it for computations, so this step of your reasoning is not clear to me.

 

[akhmeteli]

Now I think I understand your way of reasoning. You seem to think that there is a fundamental flow of time. But such a picture of time is inconsistent with superluminal motions because there are Lorentz frames in which superluminal motions appear as motions backwards in time. Therefore, the only way to make superluminal motions consistent with relativity is to adopt the BLOCK-time picture, in which time does not flow, but simply is, just like space.

Or you can interpret motions backward in time as motions of an antiparticle forward in time.

Now, to understand my way of thinking (which is generally known as the block-time or block-universe picture of spacetime), imagine that the picture I have given in #114 is not a trajectory in 1+1 dimensional spacetime, but a trajectory in 2 dimensional space (at a fixed time). Would you now agree that the dashed trajectory is unphysical?

Sorry, I don't agree, and what's worse, I don't see any reasons to agree. The entire trajectory that we have been discussing, or a similar one, can describe a real process, where a pair particle-antiparticle is created in some subprocess, and then the antiparticle is annihilated with another particle. Am I supposed to believe that if the latter particle were disturbed (say, by measurement) before the annihilation takes place, then the particle and the antiparticle that were created in the pair creation subprocess would disappear? I am not ready to accept this without serious reasons, sorry.

Another thing. I believe our discussion is not about my understanding or misunderstanding your way of thinking. I was just trying to answer your question: why your specific arguments (about BI's and CI's predictions differing in the relativistic case) cannot convince me. I hope I have explained that. As for your thinking, I guess it is possible to understand it and still not accept. Again, it may well be that your thinking is absolutely correct, and I am wrong not to accept it.

 

[Demystifier]

I believe I can "know which dashed trajectory should be attributed to a given solid trajectory." The procedure is as follows: as I know \psi(x) on M, I can compute it above M using the wave equation and use the computed dotted trajectory (although the measurement makes it unphysical, I still can compute it) to find the dashed trajectory corresponding to the physical solid trajectory. So why cannot I "use \psi(x) above M"? I certainly can use it for computations, so this step of your reasoning is not clear to me.

Well, you can use it for computations above M if you want, but you can also use some other wave function for computations above M as well. This is why I said that, according to your reasoning, above M you can use any function you want, which allows you to obtain almost any result you want. Which, of course, does not make sense.

If a function is known on M, it does NOT uniquely determine the function above M. You might say that you can determine it if you know the differential equation that this function satisfies. But the point is that, since there is interaction with the measuring apparatus above M, this differential equation is not the free Klein-Gordon equation that would be valid without the measurement. Therefore, using psi(x) above M is simply wrong (even though I cannot stop you to do it, which is why I cannot convince you that your approach is not viable).

 

[Demystifier]

Am I supposed to believe that if the latter particle were disturbed (say, by measurement) before the annihilation takes place, then the particle and the antiparticle that were created in the pair creation subprocess would disappear? I am not ready to accept this without serious reasons, sorry.

Have you ever been thinking about paradoxes (e.g. grand father paradox) related to time travel? What is your opinion on them?

My point is the following: When superluminal velocities are possible, the past cannot be changed (the pair will not disappear), but the past depends on the future (the pair will not be created in the past at all because there will be a measurement in the future). Are you ready to accept this? (Someone who accepts Bohmian nonlocality should not have problems with accepting the possibility that the future could influence the past.) In a deterministic theory this is perfectly consistent, even if it conflicts with your intuition and the notion of "free will".

By the way, if you do not accept the Bohmian interpretation but accept the collapse interpretation, then the future influences the past even at a simpler (and experimentally verified!) level of the famous delayed choice experiments.

 

[Demystifier]

How does this "mistake" translates into a wrong result? If it doesn't, this this isn't a "mistake" in the physical sense, and I think, in my case, that's all that matters. Anything beyond that, as I've mentioned, is simply a matter of tastes.

Sorry for responding so lately. What I wanted to say is the following. If you think naively about the wave function collapse, you may be inclined to think that the delayed choice is impossible. But it IS possible. So there are 2 (actually more than 2) consistent ways to think about it. You may adopt a collapse interpretation but then you must be very careful in order to avoid a mistake (a mistake that would lead to a result that contradicts experiments!), or you may adopt the Bohmian interpretation which does not require so much care in the case of delayed choice experiments.

 

[akhmeteli]

Have you ever been thinking about paradoxes (e.g. grand father paradox) related to time travel? What is your opinion on them?.

I am afraid I don't consider time travel as a possibility, other than an abstract possibility. I can see no reliable indication in physics that it can be more than that. You see, there is a great difference between something that can happen in principle and something that does happen.

My point is the following: When superluminal velocities are possible, the past cannot be changed (the pair will not disappear), but the past depends on the future (the pair will not be created in the past at all because there will be a measurement in the future). Are you ready to accept this? (Someone who accepts Bohmian nonlocality should not have problems with accepting the possibility that the future could influence the past.) In a deterministic theory this is perfectly consistent, even if it conflicts with your intuition and the notion of "free will".

By the way, if you do not accept the Bohmian interpretation but accept the collapse interpretation, then the future influences the past even at a simpler (and experimentally verified!) level of the famous delayed choice experiments.

I am afraid I cannot accept this. Not without strong arguments. And I don't feel you offer any strong arguments. You are just saying things like "there is no time flow", "the pair will not be created in the past at all", and I don't see any reasons to accept such statements. So far they look just as your point of view. Do not seem convincing to me. Furthermore, your posts fail to convince me that this is what BI predicts. Sorry.

 

[Schrodinger's Dog]

This is a bit of a sidestep and a hypothetical one at that but has anyone read Rovellis ideas about statistical "thermal" time?

He reckons time is like temperature an average or statistical representation of heat, so far the maths works but that's about all that can be said for it.

"[url[/URL]

[QUOTE=]Cosmic time

It all sounds good on paper, but is there any evidence that the idea might be correct? Rovelli and Connes have tested their hypothesis with simple models. They started by looking at the cosmic microwave background (CMB) radiation that pervades the sky - relic heat from the big bang. The CMB is an example of a statistical state: averaging over the finer details, we can say that the radiation is practically uniform and has a temperature of just under 3 kelvin. Rovelli and Connes used this as a model for the statistical state of the universe, tossing in other information such as the radius of the observable universe, and looked to see what apparent time flow that would generate.

What they got was a sequence of states describing a small universe expanding in exactly the manner described by standard cosmological equations - matching what physicists refer to as cosmic time. "I was amazed," says Rovelli. "Connes was as well. He had independently thought about the same idea, and was very surprised to see it worked in a simple calculation."

To truly apply the thermal time hypothesis to the universe, however, physicists need a theory of quantum gravity. All the same, the fact that a simple model like that of the CMB produced realistic results is promising. "One of the traditional difficulties of quantum gravity was how to make sense of a theory in which the time variable had disappeared," Rovelli says. "Here we begin to see that a theory without a time variable can not only still make sense, but can in fact describe a world like the one we see around us."

What's more, the thermal time hypothesis gives another interesting result. If time is an artefact of our statistical description of the world, then a different description should lead to a different flow of time. There is a clear case in which this happens: in the presence of an event horizon.
[/QUOTE]

[QUOTE=]
It so happens that every event horizon has an associated temperature. The best known case is that of a black hole event horizon, whose temperature is that of the "Hawking radiation" it emits. Likewise, an accelerating observer measures a temperature associated with something known as Unruh radiation. The temperature Rovelli and Connes derived matches the Unruh temperature and the Hawking temperature for a black hole, further boosting their hypothesis.

"The thermal time hypothesis is a very beautiful idea," says Pierre Martinetti, a physicist at the University of Rome in Italy. "But I believe its implementation is still limited. For the moment one has just checked that this hypothesis was not contradictory when a notion of time was already available. But it has not been used in quantum gravity."

Others also urge caution in interpreting what it all means for the nature of time. "It is wrong to say that time is an illusion," says Rickles. "It is just reducible or non-fundamental, in the same way that consciousness emerges from brain activity but is not illusory."

So if time really does prove to be non-fundamental, what are we to make of it? "For us, time exists and flows," says Rovelli. "The point is that this nice flow becomes something much more complicated at the small scale."

At reality's deepest level, then, it remains unknown whether time will hold strong or melt away like a Salvador Dali clock. Perhaps, as Rovelli and others suggest, time is all a matter of perspective - not a feature of reality but a result of your missing information about reality. So if your brain hurts when you try to understand time, relax. If you really knew, time might simply disappear.[/QUOTE]

 

[Ken G]

I was struck by this part from the above:
" Perhaps, as Rovelli and others suggest, time is all a matter of perspective - not a feature of reality but a result of your missing information about reality."
To which my reaction is, what's the big deal-- what aspect of science is not a function of our missing (versus present) information about reality? When are we going to stop being surprised that science isn't about "features of reality"? Five thousand years of history hasn't been enough to teach us that? Oh I keep forgetting-- we thought we had it right this time around.