What is the tension in a rope when a monkey accelerates up?

[rudransh verma]

Homework Statement

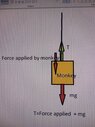
A monkey of mass m is climbing up the rope with uniform speed, the tension in the rope will be

Relevant Equations

F=ma

I think the tension in the rope will be equal to its weight , mg.
I want to ask what if the monkey accelerates up with acceleration a, then what will be the tension in the rope?

 

[phinds]

What do you think it will be and why?

 

[rudransh verma]

What do you think it will be and why?

I think whatever force monkey applies to accelerate will just add to the mg. So increased tension, mg+ma.
Monkey applies force ma in downward direction. Rope applies same opposite force on monkey. Newton’s third law. So tension is mg+ma.

 

[phinds]

Monkey applies force ma in downward direction. Rope applies same opposite force on monkey. Newton’s third law. So tension is mg+ma.

Looks to me as though you have two statements here
1) F = ma (your first two sentences)
2) F = ma +mg (your last sentence)

Which is it?

 

[rudransh verma]

2) F = ma +mg (your last sentence)

Tension in rope.

 

[phinds]

Can you draw a force diagram showing all the forces acting?

 

[rudransh verma]

Can you draw a force diagram showing all the forces acting?

 

[haruspex]

As you have been told several times, I believe, a FBD should show one system (often one rigid body) and all the forces acting on it; no internal forces. That diagram shows the gravity acting on the monkey and the monkey's force on the rope.

 

[rudransh verma]

the monkey's force on the rope.

And I think this will increase the tension.
Are you saying monkeys force is internal?
Edit: Free body diagram alone doesn't give the answer. Force applied by monkey is to be considered.
Look at the beauty of my FBD. So pretty.

 

[Lnewqban]

And I think this will increase the tension.
Are you saying monkeys force is internal?
Edit: Free body diagram alone doesn't give the answer. Force applied by monkey is to be considered.
Look at the beauty of my FBD. So pretty.

Your free body diagram should be essentially similar to the one in your other thread, because both situations are very similar.
https://www.physicsforums.com/threads/forces-within-an-elevator-cab.1009507/

The rope “feels” a heavier monkey only when the creature is accelerating upwards (monkey mass x [a+g]).

When the monkey is either hanging in a static position, or climbing at a steady pace, the rope “feels” only the natural weight (monkey mass x g).

 

[Doc Al]

And I think this will increase the tension.
Are you saying monkeys force is internal?
Edit: Free body diagram alone doesn't give the answer. Force applied by monkey is to be considered.
Look at the beauty of my FBD. So pretty.

You really need to start paying attention to @haruspex (and others).

A free-body diagram of the monkey should show only forces acting on the monkey. (Only two forces here.) Then you can apply Newton's 2nd law to those forces.

 

[phinds]

Look at the beauty of my FBD. So pretty.

Yep. Too bad beauty doesn't count and it is functionally wrong. See post #11

 

[haruspex]

And I think this will increase the tension.
Are you saying monkeys force is internal?
Edit: Free body diagram alone doesn't give the answer. Force applied by monkey is to be considered.
Look at the beauty of my FBD. So pretty.

Let me explain in more detail.

If the FBD is for the system "monkey", it should show all and only forces acting on the monkey, not forces the monkey exerts on anything else. You have shown the force the monkey exerts on the rope, when you should show the opposite force.

If the FBD is for the system "monkey+rope", it should show all and only forces acting on that system, not any forces internal to that system, so not forces between monkey and rope.

 

[rudransh verma]

You have shown the force the monkey exerts on the rope, when you should show the opposite force.

Oh yes you are absolutely right.

 

[haruspex]

Oh yes you are absolutely right.

Much better, but now you have shown it twice, once as "force from rope" and once as T.
So what equation can you write from that?

 

[rudransh verma]

Much better, but now you have shown it twice, once as "force from rope" and once as T.
So what equation can you write from that?

$T=F_{RM}+mg$ where $F_{MR}$ is force applied on monkey by rope.
Edit: @haruspex Is it right?

 

[Doc Al]

Realize that the force the rope exerts on the monkey is the tension in the rope. Don't count it twice. Only two forces act on the monkey.

 

[Steve4Physics]

No one has mentioned friction. I'd look at the system is like this:

- for the monkey climbing (or hanging onto) the rope, the only upwards force on the monkey is the upwards friction of the rope on the monkey, $F_{rm}$;

- for the rope (assumed of negligible weight), the only downwards force on the rope is the downwards friction of the monkey on the rope $F_{mr}$.

$F_{rm}$ and $F_{mr}$ are a Newton’s 3rd law pair so have equal magnitudes.

With this view, the tension doesn’t directly act on the monkey, so it should not be shown on the monkey's FBD.

Similarly, the monkey’s weight doesn’t directly act on the rope, so it should not be shown on the rope's FBD.

 

[haruspex]

Wh

$T=F_{RM}+mg$ where $F_{MR}$ is force applied on monkey by rope.
Edit: @haruspex Is it right?

What part of "but now you have shown it twice, once as 'force from rope' and once as T" did you not understand?

 

[rudransh verma]

What part of "but now you have shown it twice, once as 'force from rope' and once as T" did you not understand?

Realize that the force the rope exerts on the monkey is the tension in the rope. Don't count it twice. Only two forces act on the monkey.

I am thinking like tension in string will be how much it’s being stretched by Monkey. So in non accelerating case it’s just the weight of the monkey but otherwise it’s applying a force on the rope to pull himself up. So tension will be simply $T=F_{RM}+mg$. $F_{RM}$ is just what monkey is applying on rope.
But according to you I’ll be wrong and what you want is $T=mg+ma$

 

[haruspex]

But according to you I’ll be wrong and what you want is $T=mg+ma$

Quite so.

The flaw in your thinking is that once again you are mixing forces on different components.
Strictly speaking, tension is not a force. It is better thought of as a pair of equal and opposite forces. From the rope's perspective, those are forces tending to stretch the rope, so the force at the monkey end points down, i.e. it is the force the monkey exerts on the rope. $T=F_{MR}$.

The force the rope exerts on the monkey is equal and opposite to that. $F_{MR}=-F_{RM}$.

The only other force on the monkey is gravity, therefore in equilibrium $mg=-F_{RM}$.

 

[Doc Al]

But according to you I’ll be wrong and what you want is $T=mg+ma$

You need to stop trying to "guess" the answer. Instead, use simple physics to solve for the answer.

Here there are only two forces acting on the monkey (as @haruspex has explained many times): The rope pulling up (which can be described as the "tension" in the rope) and gravity pulling down. Now apply Newton's 2nd law to solve for that upward tension: $$\Sigma F = ma$$ $$T - mg = ma$$ thus $$T = mg + ma$$.

 

[rudransh verma]

is better thought of as a pair of equal and opposite forces.

You say pair. Are you talking about T and $F_MR$ as pair?

the monkey end points down, i.e. it is the force the monkey exerts on the rope. T=FMR.

The force the rope exerts on the monkey is equal and opposite to that. FMR=−FRM.

The only other force on the monkey is gravity, therefore in equilibrium mg=−FRM.

You are using different definition for $F_{MR} and F_{RM}$. You seem right! $F_{MR}$ is what creates tension. $T=F_{MR}=mg$ in equilibrium condition. But in accelerating case, $T=F_{MR}= mg+ma$. It’s just that in acceleration monkey applies more force which is true if we see. Tension increases!

My eqn is wrong probably because in equilibrium condition we cannot apply more force than our weight.

 

[Lnewqban]

You say pair. Are you talking about T and $F_MR$ as pair?

Copied from
https://courses.lumenlearning.com/physics/chapter/4-5-normal-tension-and-other-examples-of-forces/

“A tension is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable. The word “tension” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons. Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: “You can’t push a rope.” The tension force pulls outward along the two ends of a rope. Consider a person holding a mass on a rope as shown...”

 

[Doc Al]

“You can’t push a rope.”

One of my physics 101 professor's favorite sayings.

 

[Lnewqban]

Also, please see this old thread:
https://www.physicsforums.com/threads/trouble-with-the-concept-of-tension.985741/

 

[haruspex]

You say pair. Are you talking about T and F_MR as pair?

No, that's not what I meant.
If a rope is under uniform tension T then you could consider any short section of it as a body in its own right and find that each end is subject to a force T acting away from it. So uniform tension is like equal and opposite pairs of forces acting all the way along its length.
If the tension is not uniform (e.g. massive rope hanging vertically) then the pairs are not quite equal.

 

[rudransh verma]

end points down, i.e. it is the force the monkey exerts on the rope. T=FMR.

The force the rope exerts on the monkey is equal and opposite to that. FMR=−FRM.

Can I say $T=F_{RM}$ since T is acting everywhere.

So tension will be simply T=FRM+mg. FRM is just what monkey is applying on rope.
But according to you I’ll be wrong an

$T=F_{MR}$. So in static case $F_{MR}=mg$ due to this, $F_{RM}=mg$. Monkey moves up with constant speed.
In accelerating case, $F_{MR}=mg+ma$ due to this $F_{RM}=mg+ma$. Monkey accelerates.
Edit:
$T=F_{MR}$. So in static case $F_{MR}=-mg$ due to this, $F_{RM}=mg$. Monkey moves up with constant speed.
In accelerating case, $F_{MR}=-mg-ma$ due to this $F_{RM}=mg+ma$. Monkey accelerates.

 

[haruspex]

Can I say $T=F_{RM}$ since T is acting everywhere.

$T=F_{MR}$. So in static case $F_{MR}=mg$ due to this, $F_{RM}=mg$. Monkey moves up with constant speed.
In accelerating case, $F_{MR}=mg+ma$ due to this $F_{RM}=mg+ma$. Monkey accelerates.

That's all correct if in each case you are taking the positive direction as the direction in which you expect the force or acceleration to act. I.e. taking up as positive for $T, F_{RM}, a$, but down as positive for $F_{MR}, g$.
In some problems it might not be obvious which way some forces or accelerations (or displacements or velocities) act, so a useful practice is to fix on one direction as positive for everything, usually up. In that convention (and taking T as a force acting on the rope, so actually down) you would write:
$T=F_{MR}=-F_{RM}$ and $ma=-mg+F_{RM}$, leading to $T=-(mg+ma)$.

 

[rudransh verma]

That's all correct if in each case you are taking the positive direction as the direction in which you expect the force or acceleration to act. I.e. taking up as positive for T,FRM,a, but down as positive for FMR,g.

I took up as +ve every time.

actually down) you would write:
T=FMR=−FRM and ma=−mg+FRM, leading to T=−(mg+ma).

In post#24 in diagram we can see T is upwards , downwards, acting on the rope , is the force that stretch the rope as you said. So all these are tension.
And in your post #21 you write $T=F_{MR}$. Then in above post you write $T=F_{MR}=-F_{RM}$.
Isn't this should be $-T=-F_{MR}=F_{RM}$ taking T as the force applied on rope(taking up as +ve)?
And we can also write $T=-F_{MR}=F_{RM}$ taking T as the force the rope applies.

 

[haruspex]

In post#24 in diagram we can see T is upwards , downwards, acting on the rope , is the force that stretch the rope as you said. So all these are tension.
And in your post #21 you write $T=F_{MR}$. Then you write $T=F_{MR}=-F_{RM}$. Is this because you took Tension to be the force the monkey applies. And we can also write $T=-F_{MR}=F_{RM}$ taking T as the force the rope applies.

Yes.

I took up as +ve every time.

No you didn't. In post #28 you wrote $F_{MR}=mg$. By convention, g is always positive, so with up positive, weight is -mg. So it becomes $F_{MR}=-mg$.

 

[rudransh verma]

ctually down) you would write:
T=FMR=−FRM and

Isn't this should be $T=−F_{MR}=F_{RM}$ taking T as the force applied on rope(taking up as +ve)?

 

[rudransh verma]

No you didn't. In post #28 you wrote FMR=mg. By convention, g is always positive, so with up positive, weight is -mg. So it becomes FMR=−mg.

I used Newtons second law wrongly. I had taken the forces from different bodies when it has to be one body. We cannot apply this law here. I got you. You are merely stating the value of $F_{MR}$ as $-mg$ only. Right?
I edited the post.

 

[haruspex]

Isn't this should be $T=−F_{MR}=F_{RM}$ taking T as the force applied on rope(taking up as +ve)?

If I understand your notation, $F_{MR}$ means the force the monkey exerts on the rope. Taking T as the force applied on rope, necessarily, $T=F_{MR}$, regardless of sign convention.

 

[rudransh verma]

If I understand your notation, $F_{MR}$ means the force the monkey exerts on the rope. Taking T as the force applied on rope, necessarily, $T=F_{MR}$, regardless of sign convention.

Yeah! but T as vector is $-F_{MR}$. Right?