Ebi
- 13
- 3
- Homework Statement
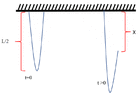
- Both ends of a rope with the mass of ρ kg/m and length of L are attached to a horizontal surface (see photo attached). At t=0, one end of the rope detaches from the surface and starts falling vertically. When this end falls the height X, what is the tension on the other end of the rope?
- Relevant Equations
- F=ma
E=U+K
and any equation in classical physics.
I have attached two different attempts to solve this problem. They both look correct to me but they give two different answers! Which one is correct, which one is wrong and why?