Angular Definition and 999 Threads
-
K
Find the angular speed of the smaller gear
1.Why does the angular speed of small gear depend only on larger gear only? 2.Why does the length of linkage connecting two gears does not have any influence on the angular speed of smaller gear? The first question can be answered by looking at slack and tightening of chain caused by rotation...- katya
- Thread
- Angular Angular speed Classical mechanics Gear Gears Speed
- Replies: 16
- Forum: Engineering and Comp Sci Homework Help
-
T
Confusion over the calculation of the angular momentum of a rigid body
Homework Statement this has been bugging me for a while now the angular momentum about any point p is given as ## \vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + L_{cm}\\ ## now if the body precessing around z axis and spinning about its own axis then angular velocity of body in lab...- timetraveller123
- Thread
- Angular Angular momentum Body Calculation Confusion Momentum Rigid body
- Replies: 20
- Forum: Introductory Physics Homework Help
-
L
Finding the angular velocity of a rotating rod
Hi everyone, sorry for bothering y'all again but here is another problem that I'm struggling with! This is the question and the professor's solution guide: When I solve the problem, I always end up getting 7.67 rad/s instead of 3.83 rad/s. My understanding of the solution is this: This is...- LuigiAM
- Thread
- Angular Angular velocity Rod Rotating Velocity
- Replies: 7
- Forum: Introductory Physics Homework Help
-

Angular Acceleration Homework: 962 Revolutions in 10 Secs
Homework Statement A computer disk starts from rest, then speeds up with angular acceleration of 190 rad/s^2. until it reaches its final speed of 7200 rpm. How many revolutions will it have made 10.0 secs after starting up? Homework Equations w = w0 + at rps = rpm / 60 1 rev = 2*pi rad 1 rad =...- Wes Turner
- Thread
- Acceleration Angular Angular acceleration
- Replies: 1
- Forum: Introductory Physics Homework Help
-

Angular momentum about a parallel axis O'
Homework Statement A system has total angular momentum L about an axis O. Show that the system's angular momentum about a parallel axis O' is given by L'=L-h×p, where p is the system's linear momentum and h is a vector from O to O'. Homework Equations L=r×p or considering a mass element...- lawsonfurther
- Thread
- Angular Angular momentum Axis Momentum Parallel
- Replies: 5
- Forum: Introductory Physics Homework Help
-
Y
Angular momentum multiple choice question
Homework Statement Hello, Here is a multiple choice question I would like to be clarified. Suppose that the angular momentum of a system can take the values 0, 1, 2. One carries out a measurement of ##J_z##,the state of the system will: ##a##-Be perfectly known if the result is 0 ##b##-Be...- yamata1
- Thread
- Angular Angular momentum Choice Momentum Multiple Multiple choice
- Replies: 18
- Forum: Advanced Physics Homework Help
-
Y
I Angular momentum state of a system
Hello, Suppose that the angular momentum of a system can take the values 0, 1, 2. One carries out a measurement of ##J_z## on this system. What can be said about the state of the system after the measurement? To what extent can it be perfectly certain if ##J_y## and ##J_x## do not commutate...- yamata1
- Thread
- Angular Angular momentum Momentum State System
- Replies: 6
- Forum: Quantum Physics
-
F
Ball rolling down an incline angular and linear acceleration
Homework Statement A ball with moment of intertia bmr^2 rolls without slipping down a plane inclined at angle O. What is it’s linear acceleration? Homework Equations Fnet= ma T = F x r T = IO’’ a = rO’’ The Attempt at a Solution Fnet = mgcos(O) - FfT = FfrT = IO’’ Ffr = bmr^2O’’ Ff =...- Fascheue
- Thread
- Acceleration Angular Ball Incline Linear Linear acceleration Rolling
- Replies: 3
- Forum: Introductory Physics Homework Help
-
F
I Can angular momentum be applied to non circular rotations?
One of the reasons I've been so stumped about learning about angular momentum in QM, is that in my classical physics class we only applied it to circular motions. Hence, while I am aware that angular momentum is connected to spherical harmonics, the orbital shapes (besides s) isn't really...- Fruit Water
- Thread
- Angular Angular momentum Applied Circular Momentum Rotations
- Replies: 2
- Forum: Quantum Physics
-
F
How Do Velocity and Friction Affect a Coin's Motion on a Table?
Homework Statement A coin stands vertically on a table. It is projected forward (in the plane of itself) with speed v and angular speed w. The coefficient of kinetic friction between the coin and the table is u. What should v and w be so that the coin comes to rest (both translationally and...- Fascheue
- Thread
- Angular Angular velocity Friction Velocity
- Replies: 3
- Forum: Introductory Physics Homework Help
-
F
Why Does Angular Velocity Appear Opposite to Linear Velocity?
I’m not quite sure where to put this post so forgive me if it’s misplaced, but can somebody explain why the angular velocity in the picture here appears to be in the opposite direction as I would expect if the velocity is in the direction that is is. I’m not looking to solve this problem...- Fascheue
- Thread
- Angular Angular velocity Velocity
- Replies: 5
- Forum: Mechanics
-

Are These Physics Questions Correct in English and Science?
hi, we are a few non-native English speaker physics teacher and we wrote some questions for an assessment book but we can't be sure about this two similar question. a) are they accurate for rules of English, are we use correct terms is there a necessary change? b) are they accurate for rules of...- bahtiyar
- Thread
- Amplitude Angular Angular displacement Displacement Simple harmonic motion Simple pendulum Swing
- Replies: 6
- Forum: Introductory Physics Homework Help
-
J
B Centrifugal Force in Angular SHM: Explained
Does centrifugal force (mv^2/r) act in any position of angular SHM? Please explain.- Jon Drake
- Thread
- Angular Centrifugal Centrifugal force Force Shm
- Replies: 4
- Forum: Other Physics Topics
-
A
Computing angular speed wrt CM I get a contradiction
Hello! I have been brushing up my Rigid Body Dynamics. I tried computing the angular speed with respect the Center of Mass (CM) using the usual split of kinetic energy and also the split of Angular momentum using the CM. First, a simple case: Two particles of mass M each separated by a distance... -
Y
Orbital/Spin angular momentum + magnetic quantum numbers
Homework Statement A single electron atom has the outer electron in a 4f1 excited state. Write down the orbital and spin angular momentum quantum numbers and the associated magnetic quantum numbers for this state. Homework Equations I don't think there is any relevant equations. I think it...- youngfreedman
- Thread
- Angular Angular momentum Electron Magnetic Momentum Numbers Quantum Quantum numbers
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Momentum transfer from linear to angular motion
I am trying to create a momentum trap to calculate the velocity of a projectile when it hits the trap. It essentially consists of a plate if known mass at the bottom of a pendulum of known radius. When the projectile hits the plate, the degrees that the pendulum rotates are recorded. I believe... -
S
Show the relationship between torque and angular momentum
<Moderator's note: Moved from a technical forum and thus no template.> I am trying to design and perform a physics lab. It needs to show the relationship between torque and angular momentum. I have gotten as far designing a 4" PVC coupling and have it on a ramp. I am not sure where to go from here.- Shank
- Thread
- Angular Angular momemtum Angular momentum Momentum Relationship Torque
- Replies: 3
- Forum: Introductory Physics Homework Help
-

Angular momentum and rotational energy
Homework Statement A school playground has a carousel, which is simply a circular platform that can rotate around its center axis with negligible friction. This carousel has radius r=1.6 m and rotational inertia I= 177m^2kg. Suppose you are standing beside the carousel which is already spinning...- starstruck_
- Thread
- Angular Angular momentum Energy Introductory physics Momentum Rotational Rotational energy
- Replies: 2
- Forum: Introductory Physics Homework Help
-
N
Angular Momentum of a hydrogen atom in the 7f state
Homework Statement A hydrogen atom is in the 7f state. What is the magnitude of its orbital angular momentum? Homework Equations L=sqrt(L(L+1)hbar The Attempt at a Solution L= Sqrt(3(3+1)Hbar) 1.41hbar (we want J*S) 1.41*1.054*10^-34 1.47*10^-34J*S- Noreturn
- Thread
- Angular Angular momentum Atom Hydrogen Hydrogen atom Momentum State
- Replies: 3
- Forum: Introductory Physics Homework Help
-
M
I Measurement Values for z-component of Angular Momentum
Given a wave function $$\Psi(r,\theta,\phi)=f(r)\sin^2(\theta)(2\cos^2(\phi)-1-2i*\sin(\phi)\cos(\phi))$$ we are trying to find what a measurement of angular momentum of a particle in such wave function would yield. Attempts were made using the integral formula for the Expectation Value over a...- MoAli
- Thread
- Angular Angular momemtum Angular momentum Measurement Momentum Operator Operators Quantum mechahnics Wavefunctions
- Replies: 1
- Forum: Quantum Physics
-
C
MHB How Does Air Resistance Affect Power in Rotational Motion?
[FONT=verdana]A sphere of mass 1.9 kg and radius 0.5 m is attached to the end of a massless rod of length 3.0 m. The rod rotates about an axis that is at the opposite end of the sphere (see below). The system rotates horizontally about the axis at a constant 422 rev/min. After rotating at this...- cbarker1
- Thread
- Angular Power System
- Replies: 1
- Forum: General Math
-
W
Elliptical Orbits and Angular Momentum
Homework Statement Why is the magnitude of Angular Momentum for an elliptical orbit as such? $$l = mr^2\dot{\phi}$$ where ##\dot{\phi}## represents angular momentum. I have always assumed that angular momentum was $$l = r \times P = mr \times V = mrVsin(\theta) = mr^2\dot{\phi} sin(\theta)$$...- WWCY
- Thread
- Angular Angular momentum Momentum Orbits
- Replies: 7
- Forum: Introductory Physics Homework Help
-
W
Self-Induced Emf and Angular Frequency
The context is an ac circuit with only one element - the inductor. My textbook says that the self-induced emf increases with increasing angular frequency, but I'm having trouble seeing this mathematically. If self-induced emf = ε = -L(dI/dt) and L = X/ω, then emf and ω are inversely related...- waley
- Thread
- Angular Angular frequency Emf Frequency Inductor Self inductance
- Replies: 2
- Forum: Electromagnetism
-

Angular momentum and rotational inertia
Homework Statement You decide to design a bicycle that will have only 3/4 of the angular momentum of the original wheel when both wheels are traveling along a road at the same velocity. The original wheel had a diameter of d1=37cm and rotational inertia of I1=0.32 m2kg. If your new wheel has a...- starstruck_
- Thread
- Angular Angular momentum Inertia Momentum Rotational Rotational inertia
- Replies: 25
- Forum: Introductory Physics Homework Help
-
R
Why is conservation of angular momentum failing in this case
https://drive.google.com/file/d/1Z-avhDqYbxDtMzk6Rv_NES7rIvDmzMPz/view?usp=drivesdk 2.conservation of angular momentum 3.for the above question I tried applying conservation of angular momentum about the point of contact where the cyclinders touch each other but my answer does not match with...- Roxas ross
- Thread
- Angular Angular momentum Conservation Failing Momentum
- Replies: 4
- Forum: Introductory Physics Homework Help
-
S
Angular velocity of a wheel rolling around a fixed axis
Mentor note: Moved to homework section[/color] A conical wheel is rolling (without slipping) around a fixed axis OZ as shown in the figure. The velocity of point C is vc = at. The direction of the velocity of C is shown by a cross i.e. along negative x-axis. We have to find the angular...- sid0123
- Thread
- Angular Angular velocity Axis Rolling Velocity Wheel
- Replies: 1
- Forum: Advanced Physics Homework Help
-
C
MHB Find accelerations- Angular and linear
[FONT=verdana]Dear Every Body, I need some help. First question: Is the tension of the string is the same or different? A pulley of moment of inertia 2.7 kg [FONT="]· m2 is mounted on a wall as shown in the following figure. Light strings are wrapped around two circumferences of the pulley...- cbarker1
- Thread
- Angular Linear
- Replies: 10
- Forum: General Math
-
S
Conservation of Angular Momentum and a Spinning Bicycle Wheel
A person standing on a stationary friction-less turntable spins a bicycle wheel with the rotation axis of the wheel in the horizontal direction, thus the initial angular momentum is in the horizontal direction (x - axis), say to the right. Now suddenly the person turns the axis of rotation of...- samirgaliz
- Thread
- Angular Angular momentum Bicycle Conservation Momentum Spinning Wheel
- Replies: 5
- Forum: Mechanics
-

Doubt on conservation of angular momentum
Homework Statement A uniform thin rod of length ##2l## and mass ##m## lies on a horizontal table. A horizontal impulse ##J## is given to the rod at one end. There is no friction. The total kinetic energy of the rod after impulse will be ? Homework Equations ##Jl=I\omega## ##J=mv_{cm}##...- ubergewehr273
- Thread
- Angular Angular momentum Conservation Doubt Momentum Rotational mechanics
- Replies: 8
- Forum: Introductory Physics Homework Help
-
A
Angular Velocity in Simple Harmonic Motion
I am very confused about angular velocity ω and why its used in simple harmonic motion. ω is described as θ/τ but when it comes to masses on springs, there is no angle - it is zero. Angular velocity comes from circular motion but the motion of SHM is not circular. My confusion is even greater...- Abu
- Thread
- Angular Angular velocity Circle Displacement Harmonic Harmonic motion Motion Simple hamonic motion Simple harmonic motion Velocity
- Replies: 11
- Forum: Mechanics
-
J
Why Is the Calculated Angular Momentum of the Pucks Zero?
Homework Statement Three small, identical 0.70-kg pucks are attached to identical 0.50-m strings, tied together at a common center as shown in (Figure 1) . Pucks are whirled in circular motion at angular speed 3.0 s-1 What is the magnitude of the angular momentum of the system about the...- Joshua A
- Thread
- Angular Angular momemtum Angular momentum Momentum Vectors
- Replies: 5
- Forum: Introductory Physics Homework Help
-
T
How to solve for the moment of inertia and angular acceleration?
A girl is climbing up a set of stairs and has her femur horizontal. Her thigh weighs 12 pounds, acting at a center of mass 15 cm from her hip joint. She places 50 pounds of weight on the lower portion of that leg, vertically through her knee. Her gluteus maximus is applying a force directed 30...- tellas
- Thread
- Acceleration Angular Angular acceleration Force Inertia Moment Moment of inertia
- Replies: 21
- Forum: Introductory Physics Homework Help
-
S
Angular Momentum of a Ball at Half Height
Homework Statement In the figure, a 0.400 kg ball is shot directly upward at initial speed 58.3 m/s. What is its angular momentum about P, 1.42 m horizontally from the launch point, when the ball is (a) at maximum height and (b) halfway back to the ground? What is the torque on the ball about P...- ScreamingIntoTheVoid
- Thread
- Angular Angular momentum Ball Momentum
- Replies: 9
- Forum: Introductory Physics Homework Help
-
S
Rotational Inertia and Angular Momentum
Homework Statement A disk with a rotational inertia of 8.38 kg·m2 rotates like a merry-go-round while undergoing a torque given by τ = (5.03 + 1.01t) N · m. At time t = 1.00 s, its angular momentum is 6.57 kg·m2/s. What is its angular momentum at t = 3.00 s? Homework Equations dL/dt= T...- ScreamingIntoTheVoid
- Thread
- Angular Angular momentum Inertia Momentum Rotational Rotational inertia
- Replies: 2
- Forum: Introductory Physics Homework Help
-
R
I Angular momentum of the Universe
It explains very well many aspects of the Universe. Why should there be any angular momentum though? The idea that the Universe is itself intrisically rotating doesn't make sense. -
T
Applied Angular Velocity & Acceleration
Hey guys, I'm working on a product that rotates cups around a shaft, I am trying to calculate the torque required to do so. I have given it my best shot below, does this seem right to you? The Main Shaft Motor will need to rotate holder one from the filling cups position to the pressing lids...- TJS
- Thread
- Acceleration Angular Angular velocity Applied Velocity
- Replies: 6
- Forum: Mechanics
-

Why velocity can change when angular momentum is conserved?
Why the tangential velocity of a particle increase if there are no external torque acting on it and its angular momentum is conserved? I know that L = I.ω (angular momentum equals moment of inertia times angular velocity) and v = ω.r (tangential velocity equals angular velocity times the...- CollinsArg
- Thread
- Angular Angular momentum Change Momentum Tangential velocity Velocity
- Replies: 7
- Forum: Mechanics
-
A
What is the angular acceleration of the rod?
Homework Statement A thin, uniform, 18.5 kg post, 2.10 m long, is held vertically using a cable and is attached to a 5.00 kg mass and a pivot at its bottom end (as shown below). The string attached to the 5.00 kg mass passes over a massless, frictionless pulley and pulls perpendicular to the...- Asad Raza
- Thread
- Acceleration Angular Angular acceleration Moment of inertia Rod Rotation Torque
- Replies: 18
- Forum: Introductory Physics Homework Help
-
What is the need of angular frequency in S.H.M.?
While studying S.H.M., I found that the term ##\omega## is used quite a lot. The book says that this ##\omega## is the angular frequency. What is this angular frequency? Why do we use ##\omega## rather than ##\nu##, that is, the normal frequency? All equations in S.H.M. are made with ##\omega##...- Wrichik Basu
- Thread
- Angular Angular frequency Frequency Simple hamonic motion
- Replies: 2
- Forum: Electromagnetism
-
T
Angular velocity of rod supported by yoyo
Homework Statement Homework EquationsThe Attempt at a Solution so since the rod and the floor is tangent to the circle then the tangent at external point theorem can be applied to find out that the two triangles are congruent i assumed the the circle start out with tangent to the y-axis at...- timetraveller123
- Thread
- Angular Angular velocity Rod Velocity
- Replies: 10
- Forum: Introductory Physics Homework Help
-
N
Centripetal Acceleration Problem: Finding Angular Speed
Hi all, I've been lurking around the forums for a while to get help with homework but I figured I'd finally make an account to get direct feedback. I'm having problems with this centripetal acceleration problem, Homework Statement "In an old-fashioned amusement park ride, passengers stand...- Nahtee
- Thread
- Acceleration Angular Angular speed Centripetal Centripetal acceleration Speed
- Replies: 2
- Forum: Introductory Physics Homework Help
-
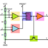
Calculate the angular velocity and angular acceleration (pendulum)
Homework Statement 13.53 The tension in the sting of the simple pendulum is 7.5N when θ=30deg. Calculate the angular velocity and angular acceleration of the string at this instant. Homework EquationsThe Attempt at a Solution Is this correct?- Alexanddros81
- Thread
- Acceleration Angular Angular acceleration Angular velocity Cylindrical coordinates Kinetics Pendulum Velocity
- Replies: 1
- Forum: Introductory Physics Homework Help
-
M
Angular Velocity & Acceleration for a Series of Connected Objects
https://drive.google.com/file/d/0B0NXDy0RMDe7MXhMcjZBdkhoSDg/view?usp=sharing PIC: [https://drive.google.com/file/d/0B0NXDy0RMDe7MXhMcjZBdkhoSDg/view?usp=sharing] 1. A rotating disk is connected with two arms AD and DB which are rotating with the rate of 0.2 rad/s^2 and -0.3 rad/s^2...- Mandex Chak
- Thread
- Acceleration Angular Angular acceleeation Angular velocity Rotating disk Series Velocity
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Question about Angular Motion in a horizontal plane
For finding the critical speed or the minimum speed in a question for a vertical plane, you take either the friction or the contact (normal) force to be 0, so F=W However, for a horizontal plane, like spinning something around in a circle, you can still do F=W to find the critical speed or the...- sodnaz
- Thread
- Angular Angular motion Horizontal Motion Plane
- Replies: 2
- Forum: Mechanics
-
C
Angular velocity of cylinders after slipping over each other
Homework Statement two cylinders of radii r1, and r2 having moments of inertia I1, and I2, about their respective axes. Initially, the cylinders rotate about their axes with angular speeds w1, and w 2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes...- carlyn medona
- Thread
- Angular Angular velocity Cylinders Slipping Velocity
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Determine the angular speed ##\dotθ## of the arm OC
Homework Statement 13.30 The colar B slides along a guide rod that has the shape of the spiral R = bθ. A pin on the collar slides in the slotted arm OC. If the speed of the collar is constant at v0, determine the angular speed ##\dot θ## of the arm OC in terms of v0, b, and θ. Homework...- Alexanddros81
- Thread
- Angular Angular speed Arm Kinematics Polar coordinates Speed
- Replies: 3
- Forum: Introductory Physics Homework Help
-
A
Does a rotating rigid body has single angular velocity.
Hello all, First of all I want to mention what believe or result of concepts, do I hold about rotational motion especially about the angular velocity. I assume that unlike velocity angular velocity has to worked out from some point. I will begin with particle for this I assume that the question...- Ahsan Khan
- Thread
- Angular Angular velocity Body Rigid body Rotating Velocity
- Replies: 3
- Forum: Mechanics
-
U
Angular momentum of a pulley system
Homework Statement it is given in the image i uploaded Homework Equations L→=r→ × p→[/B] The Attempt at a Solution If the angular momentum of a particle is the cross product of the position vector of the particle from the axis and its linear momentum, how can the angular momentum of m1 and...- undividable
- Thread
- Angular Angular momemtum Angular momentum Momentum Pulley Pulley system System
- Replies: 9
- Forum: Introductory Physics Homework Help
-

A question about angular momentum and torques....
There is something I don't quite understand about the law of conservation of angular momentum. Let's say a person is rotating about an axis passing through his/her centre of mass, with an angular speed speed ω1, and has a rotational inertia I1 about about the centre of mass. No torque is acting...- NoahCygnus
- Thread
- Angular Angular momentum Momentum Torques
- Replies: 6
- Forum: Mechanics
-
M
Understanding DTFT Angular Frequency: Mike's Questions
Hello everyone. Iam trying to understand the discrete time Fourier transform for a signal processing course but Iam quite confused about the angular frequency.If I have a difference equation given, what values should I choose for my angular frequency if I do not know anything about the sample...- MikeSv
- Thread
- Angular Angular frequency Dtft Frequency
- Replies: 4
- Forum: Electrical Engineering