Axis Definition and 895 Threads

Lior Shamir reports an apparent preferred galactic spin axis based on his examination of data from the JWST Advanced Deep Extragalactic Survey (JADES). His report is available in an article in Monthly Notices of the Royal Astronomical Society. The pattern is not subtle (N=263, sigma=3.39) and...

Alright, I've been wondering this for a while now. Say you have an infinite grid of squares in hyperbolic geometry, such that the curvature makes it so each angle of each square is 72° (5 squares at each corner). At the very 'center' of the grid, or the origin, there would be 5 straight rays...

In many homework problems I've encountered, they all seem to assume the electric field = 0 point is along the axis of the two charges. Intuitively it kind of makes sense, but I'm looking for a solid justification for it. In other words, why can't it be off the axis of the two charges? When...

i have this linkage as far as happening that This Link make angle between x-y axis and rotate also between x-y axis , meanwhilel yaw( z-axis) am i right ? please make it clear

so calculated, the moment of inertia for a rod about an axis at the end of the rod is I = 1/3 * M * L^2 here for case 1: arms to the side I is calculated to be ##I = 0.224## for case 2: arms stretched ## I = 1 / 3 * M * L^2 + M * d^2 ## with L = 0.6 m (length of rod) and d = 0.2 (dinstance from...

[Mentor Note: See post #10 below for an updated problem statement using LaTeX and with a better drawing] what i want is to find the axis of rotation when the centre of gravity and point on which external force is acting is given along with the magnitude and direction of force. In the example...

Recently, I’ve heard from Anton Petrov on YouTube that some tidally-locked planets around red-dwarf stars (such as TRAPPIST-1) have been suspected to flip around their own axis every once in a while — so that the former day side becomes the night side, and vice versa. This is presumed to happen...

I want to know if there is any proper relation between the angles of a vector with the three dimensional coordinate axes, if the angles are ,α , β and γ, will the sum of α, β and γ be 180 degress that is α + β + γ = 180°,m finding the same to be true in a 2 D case where α + β = 90° and γ =...

For this problem, How do we calculate the moment of inertia of (2) and (3)? For (3) I have tried, ##I_z = \int r^2 \, dm ## ## ds = r ## ##d\theta ## ##\lambda = \frac {dm}{ds}## ##\lambda ## ##ds = dm ## ## \lambda r ## ##d\theta = dm ## ##I_z = \lambda \int r^3 d\theta ## ##I_z = \lambda...

Hi, unfortunately, I am not getting anywhere with task b In the lecture we had the special case that ##\vec{M}=0## , ##I_x=I_y=I , I \neq I_z## and ##\omega_z=const.## Then the Euler equation looks like this. $$I_x\dot{\omega_x}+\omega_y \omega_z(I_z-i_y)=0$$ $$I_y\dot{\omega_y}+\omega_z...

What I have done is on my Ipad that I cant upload or at least don't know how to... :/ With hope of help DJ

The net torque about an axis through point A is given by, If I take the axis of rotation perpendicular to the paper and the solution I arrive would be the following below Net torque = 30 cos45 x 1.5 - 10 cos30X 3 = 5.829Nm ( counterclockwise) But the book gives an answer...

Angular Momentum and Torque are defined about a point. But Moment of Inertia of a body is defined about an axis. There are equations which connect Angular momentum and Torque with Moment of Inertia. How will this be consistent? When I say that the torque of a force acting on a body about a point...

Summary: A 5.0- cm -diameter cylinder floats in water. How much work must be done to push the cylinder 11 cm deeper into the water? F =Aρgx A 5.0- cm -diameter cylinder floats in water. How much work must be done to push the cylinder 11 cm deeper into the water? F =Aρgx x being the...

Answer should be (c) 32,7 ##\frac{m}{s^2}## My attempt: ##\omega_{2\pi}## -> ##\omega## after 1 revolution ##\omega_{2\pi} = 0,2 * (2\pi)^2## ##\omega_{2\pi} = 7,9 \frac{rad}{s}## ##\frac {d}{dt}\omega = \alpha = 0,2*2*\theta## ##\alpha_{2\pi}## -> ##\alpha## after 1 revolution...

This video demonstrates the Dzhanibekov effect (instability when spinning arround the intermediate axis). In order to achieve the best results, is it better for the three MoI's to be close together, or for them to have widely differing values?

Hi, I have an object sitting on the ground, with a coefficient of friction (COF) of 0.3. Lets say it is a square block, and will rotate on its central axis. How much torque is required to rotate this block? I am ignoring inertia weights as will be rotating very slowly.I can solve my problem by...

I am using the following formula to solve this problem. $$ L_a= L_c + \text { (angular momentum of a particle at C of mass M)}$$ Because the point C is at rest relative to point A, so the second term in RHS of above equation is zero. Hence, the angular momentum about A is same as angular...

I have come up with two different approaches, but I'm not sure which one is correct since they give different answers. We use the following equation to get the total moment of inertia. ##I_o## = moment of inertia of disk about O axis + moment of inertia of road about O axis Approach 1...

On this graph on the Y-axis just above the origin is a "zigzag" mark (highlighted with the red circle) which represents a discontinuity as the value of Y jumps from 0 to 130. Does this mark have a formal name?

A friend of mine shared a YouTube video with me, saying he was sure I would love it. He described it as very strange with a rotating wingnut in the space station flipping over on its rotation axis, over and over, while it spun rapidly. After watching the video, I verified I was taught the...

$$I = \int{r^2dm}$$ $$dm = \sigma dV$$ $$dV = 4\pi r^2dr$$ $$\sigma = \frac{M}{\frac{4}{3}\pi*R^3}$$ $$I = \sigma 4 \pi \int_0^R{r^4 dr} = \frac{3*MR^2}{5},$$ which is not the correct moment of inertia of a sphere

When we take the x-axis parallel to incline surface its clear that the horizontal component of weight is causing the block to come down but when we take the standard orientation its not so clear to me. Is horizontal component of ##F_N## causing the block to come down? <Moderator's note: Use of...

We know that $$V_Z=\int_{\textrm{ring}} E\cdot dl$$ We therefore consider ##E=\dfrac{\lambda}{2\pi \varepsilon_0}\cdot \dfrac1r##. Then, $$V_Z=\int_{\textrm{ring}} \dfrac{\lambda}{2\pi \varepsilon_0}\cdot \dfrac1r\, dl = \dfrac{\lambda}{2\pi \varepsilon_0}\dfrac1r \int_{\textrm{ring}}dl=$$...

Hi, When you have a one-dimensional plane, such as x-axis plane, when you move, you coordinates will change along all given axes. Actually, there is only one dimension available in this case so it doesn't make much sense here. When you have two-dimensional plane, such as x-y plane, when you...

Case 1 worked out great, I found it to be linearly polarized light at an angle ##\alpha = \frac{\pi}{4}##, but Case 2 is giving me trouble. As best I can tell, ##\alpha## is undefined in case 2. How do I solve case 2?

Since the question says that "velocity along the cylinder axis" and "magnetic field perpendicular to the cylinder axis". So cross product of velocity and magnetic field becomes their magnitude. ##\vec v\times \vec B=||v|| \\ ||B||## So ##\vec F=qvB## ##mg=qv\frac{\mu_0 nI}{4\pi r}## At first...

I'd appreciate if someone could check whether my work is correct. The ##x##-##y## symmetry of the aperture separates the Fresnel integral:\begin{align*} a_p \propto \int_{-a/2}^{a/2} \mathrm{exp}\left(\frac{ikx^2}{2R} \right) dx \int_{-a/2}^{a/2} \mathrm{exp}\left(\frac{iky^2}{2R} \right) dy...

I'm now learning about rotational motion without slipping and it's really hurting my brain to think about. Imagine a cylinder rotating on a flat plane. I can accept that there is both translational and rotational motion. For example, a given point on the circumference of the cylinder follows a...

Summary:: Averaging (a power of) semimajor axis to position ratio wrt to time - celestial mechanics I evaluated it this far, but i don't know how to change the dt to d theta ... the final solution is supposedly (1-e^2)^-(3/2) . Any help will be appreciated. [Image re-inserted with correct...

If I choose my axis of rotation for torque analysis to be the left-end of the plank, I can get the correct results. If I instead choose the com point -- I run into a dead end. Is there a way of a priori knowing this would happen? Thank you.

If a system is represented by a set of generalized coordinates ##q_i## in which one coordinate say ##\theta## is such that ##d \theta## represents a rotation of the system about a fixed axis( an axis whose orientation remains fixed in space) then the kinetic energy ##T## shouldn't depend on it...

Hi all, It has been some time since I've done physics. I wish to model some projectile motion of a lure being cast from a fishing rod. The setup is very similar to that of a trebuchet. The fishing rod - we'll assume a perfectly rigid beam - is rotating about a fixed axis. I can calculate...

Hi all! In this assignment I have to formulate an equation for the shortest distance from a point on a circle perimeter to an arbitrary axis in a circle with angle theta. I included an image with the sketch. Anyone that can help?

This question I have been thinking for some time. 1. For an Aircraft we have 4 types of motion. Yaw, Pitch, Roll and Forward Velocity. 2. For a Locomotive, we can say there are only Forward Velocity. No other axis of motion. 3. For a Car, we have the Forward Velocity and Yaw motion (steering...

A simulation/animation/explanation based on the inertial frame only: The previous videos referenced there are here: See also this post for context on the Veritasium video: https://mathoverflow.net/a/82020 Note to mods: The previous thread is not open anymore so I opened a new one. Feel free...

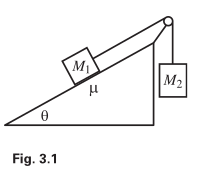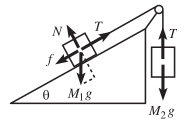><br/> >Mass M1 is held on a plane with inclination angle θ, and mass M2 hangs over the side. The two masses are connected by a massless string...

I'm trying to model the linear collision of a bat and a ball using the conservation of angular momentum. The ball is a point particle with at rest wrt the axis of rotation, and the bat is being treated as a rod of negligible radius. I have had to work through several problems involving a ball...

Kleppner and Kolenkow say "Consider a gyrocompass consisting of a balanced spinning disk a light frame supported by a horizontal axle. The assembly is turntable rotating at steady angular velocity Ω. There cannot be any torque along the horizontal AB axis because the axle is pivoted". I'm not...

Hello, Given the figure below, and the following statement: "The robot arm is driven by two hydraulic cilinders A and B which brings point D rotates CW. The gear in point D has a angular velocity of 5 rad/s. Calculate the velocity and acceleration of the part in point C." First I determined...

Now, i am extremelly confused about all this thing. More preciselly, i can't understand how 1.29 was obtained. It was used the A representation? How do he uses it? There is something to do with the canonical basis?

If the crawling insect were stationary at a certain instant of time, then it would have the same angular velocity as that of disk, which is w in a clockwise direction. But now it's velocity at any instant is the vector sum of velocity due to rotation and the velocity it crawls at. My attempt is...

I = 2/5M R^2 + Md^2 This is analagous to Earth's movement about the Sun. Is the moment of inertia of Earth about the centre of mass of the Earth Sun system = 2/5MR^2 + Md^2, where: M = Mass of earth, R = Radius of Earth, d = distance from Earth to centre of mass of earth-sun system.

So here is what I'm trying to do. The values on x-axis are from 10000, 20000, 30000, ... 100000. I'm trying to write it like this: 10, 20, 30, 40, ... 100 (only x axis) But how do I do this? I've tried those two examples How to scale the axis in Gnuplot, How to scale the axes in Gnuplot but...

Hi I would like to transform the S-parameter responce, collected from a Vector Network Analyzer (VNA), in time domain by using the Inverse Fast Fourier Transform (IFFT) . I use MATLAB IFFT function to do this and the response looks correct, the problem is that I do not manage to the time scaling...

The only thing I can think of is that to create a circularly polarized wave the axes of the quarter wave plate will have to be at 45 degrees to the E vector. Only then it can have both components on the slow and fast axis equal. Then the slow axis will cause delay and the resulting vector will...

So i derived the moment of inertia about the axis of symmetry (with height h) and I am confused about the perpendicular axis theorem. The problem ask to find the moment of inertia perpendicular to axis of symmetry So the axis about h, i labelled as z, the two axis that are perpendicular to z, i...

Does the Earth flip on its axis? I know the magnetic field will flip every 200,000 years or so but I am asking about the entire earth. I have made a model of an Earth by drilling 2 perpendicular holes in a pool cue ball, filling them with lead and spinning it in a cushion of compressed...

Hello, there. A friend asked me a problem last night. Suppose that a system consists of a rod of length ##l## and mass ##m##, and a disk of radius ##R##. The mass of the disk is negligible. Now the system is rotating around an axis in the center of the disk and perpendicular to the plane where...