You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Theorem Definition and 1000 Threads
-

B Mean-Value Theorem, Taylor's formula, and error estimation
Hi, PF Taylor's formula provides a formula for the error in a Taylor approximation ##f(x)\approx{P_{n}(x)}## similar to that provided for linear approximation. Observe that the case ##n=0## of Taylor's formula, namely, ##f(x)=P_{0}(x)+E_{0}(x)=f(a)+\dfrac{f'(s)}{1!}(x-a)##, is just the...- mcastillo356
- Thread
-
- Tags
- Error Estimation Formula Theorem
- Replies: 3
- Forum: Calculus
-

A Confused by a theorem in Milnor-Stasheff
The k-th Pontrjagin class of a real vector bundle is defined as the 2k-Chern class of the complexified bundle. Therefor, a Pontrjagin class lives in cohomology with integer coefficients. But then the statement of Theorem 15.9 is that if the coefficient ring is taken to be a PID \Lambda...- quasar987
- Thread
- Replies: 4
- Forum: Topology and Analysis
-

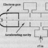
Engineering Question about a circuit to be solved with Norton's theorem
Hello guys, I am new here. I was wondering whether I could get some help about the highlighted part. What I don't understand is why we are able to ignore the 5-ohms resistor when we have short circuited terminals a-b. Thanks in advance.- link223
- Thread
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-
Intermediate Axis Theorem.... fun to learn it again with You Tube
A friend of mine shared a YouTube video with me, saying he was sure I would love it. He described it as very strange with a rotating wingnut in the space station flipping over on its rotation axis, over and over, while it spun rapidly. After watching the video, I verified I was taught the... -
B
I Does Axler's Spectral Theorem Imply Normal Matrices?
Going through Axler's awful book on linear algebra. The complex spectral theorem (for operator T on vector space V) states that the following are equivalent: 1) T is normal 2) V has an orthonormal basis consisting of eigenvectors of T and 3) the matrix representation of T is diagonal with...- boo
- Thread
- Replies: 3
- Forum: Linear and Abstract Algebra
-

Finding the Wrong Answer with Stokes' Theorem
From Stokes' theorem: ##\int_{C}^{}\vec F\cdot d\vec r=\iint_{S}^{}curl\vec F\cdot d\vec S=\iint_{D}^{}curl\vec F\cdot(\vec r_u \times \vec r_v)dA ## To get to the latter surface integral, I started by parametrizing the triangular surface in ##uv## coordinates as: $$\vec r=<1-u-v,u,v>, 0\leq...- greg_rack
- Thread
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Calculating the Line Integral of F over C: Stokes' Theorem and Symmetry
From Stokes we know that ##\iint_{\textbf{S}}^{}curl \textbf{F}\cdot d\textbf{S}=\int_{C}^{}\textbf{F}\cdot d\textbf{r}##. Now, we can calculate the surface integral of the curl of F by calculating the line integral of F over the curve C. The latter ends up being 0(I calculated it parametrizing...- greg_rack
- Thread
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
O
I Equipartition theorem and Drag
If I have a many-body Hamiltonian, and I choose a coordinate x with canonical momentum p, I can say that by the generalized equipartition theorem that <p(dH/dx)> = -<p(dp/dt)> = 0 Since p and x are distinct phase space variables, and since by the Hamiltonian equations of motion the force...- Opus_723
- Thread
- Replies: 2
- Forum: Classical Physics
-
H
Kinematic Problem w/ Parabola: Solving w/ KE Theorem?
This is not really a homework problem (it could be made to be though). I kind of made it up, inspired by a youtube math challenge problem involving parabolas, a water fountain where A = 1, R = 3, and H = 3. The solution given (h = 9/4) was based off simple math utilizing vertex form of a...- h1a8
- Thread
- Replies: 25
- Forum: Introductory Physics Homework Help
-
C
I Where to find this uniqueness theorem of electrostatics?
There is a nice uniqueness theorem of electrostatics, which I have found only after googling hours, and deep inside some academic site, in the lecture notes of Dr Vadim Kaplunovsky: Notice that the important thing here is that only the NET charges on the conductors are specified, not their...- coquelicot
- Thread
- Replies: 27
- Forum: Classical Physics
-
L
[Bayes' Theorem] Finding the probability of guessing correctly
I calculated the probability of box 1/2/3 given white. P(Box 1 | white) = P(Box 1)*P(White | Box 1)/(P(Box 1)*P(White | Box 1) + P(Not Box 1)*P(White | Not Box 1)) = ((1/3)*(1/2)) / (((1/3)*(1/2) + (2/3)*(5/7) = 7/27 P(Box 2 | white) = P(Box 2)*P(White | Box 2)/(P(Box 2)*P(White | Box 2) +...- LokLe
- Thread
-
- Tags
- Probability Theorem
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-

A Interpretations of the No Communication Theorem
Moderator's note: Spin-off from previous thread due to topic change. Not in the sense in which it is used in the no communication theorem. That sense is basically the information theoretic sense, which in no way requires humans to process or even be aware of the information.- PeterDonis
- Thread
- Replies: 47
- Forum: Quantum Interpretations and Foundations
-

Understanding the Mean value theorem
Can we have two tangents (two turning points) within the given two end points just asking? I know the theorem holds when there is a tangent to a point ##c## and a secant line joining the two end points. Or Theorem only holds for one tangent point. Cheers- chwala
- Thread
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Green's reciprocity theorem about current density and magnetic field
I have to prove three equations above. For first two equations, I've been thought and made reasonable answer by using a definition of the electricfield. However, for third, I can't use a definition of a magnetic field due to the cross product Like J_2 X J_1 X (r_2 - r_1). I think three of 'em...- SanaiBongchul
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
E
A The Factorization Theorem in Particle Physics
I have been tasked with calculating amplitudes of a B meson decaying to a photon and lepton/lepton anti-neutrino pair ,upto one loop and have pretty much never seen this thing before. I will ask my questions along the way as I describe what I am doing. This factorization theorem seems to go thus...- Elmo
- Thread
- Replies: 6
- Forum: High Energy, Nuclear, Particle Physics
-
H
I How is uniqueness about the determinant proved by this theorem?
Let me first list the four axioms that a determinant function follows: 1. ## d (A_1, \cdots, t_kA_k, \cdots, A_n)=t_kd(A_1, \cdots A_k, \cdots, A_n)## for any ##A_k## and ##t_k## 2. ##d(A_1, \cdots A_k + C , \cdots A_n)= d(A_1, \cdots A_k, \cdots A_n) + d(A_1, \cdots C, \cdots A_n)## for any...- Hall
- Thread
- Replies: 10
- Forum: Linear and Abstract Algebra
-

B Work energy theorem by variable force
Its Good to be Back! From Resnik, Fundamentals of physics: Consider a particle of mass m, moving along an x-axis and acted on by a net force F(x) that is directed along that axis. The work done on the particle by this force as the particle moves from position ##x_i## to position ##x_f## is given...- rudransh verma
- Thread
- Replies: 23
- Forum: Mechanics
-
P
I Mean value theorem - prove inequality
I don't need an answer (although I don't have sadly, it's from a test). I need just a tip on how to start it... i cannot use Taylor in here (##\ln(x)## is not Taylor function), therefore, its only MVT, but I don't know which point I should try... since I must get the annoying ##\ln(x)##...- physics1000
- Thread
- Replies: 19
- Forum: Calculus
-

MHB Checking Proof of Theorem 6.2.8 Part (ii)
I have completed a formal proof of D&K Theorem 6.2.8 Part (ii) ... but I am unsure of whether the proof is correct ... so I would be most grateful if someone could check the proof and point out any errors or shortcomings ... Theorem 6.2.8 reads as follows: Attempted Proof of Theorem 6.2.8...- Math Amateur
- Thread
- Replies: 2
- Forum: Topology and Analysis
-

MHB How can we prove the inequality for the supremum and infimum of f*g and f*g?
I am reading J. J. Duistermaat and J. A. C. Kolk: Multidimensional Analysis Vol.II Chapter 6: Integration ... I need help with the proof of Theorem 6.2.8 Part (iii) ...The Definition of Riemann integrable functions with compact support and Theorem 6.2.8 and a brief indication of its proof...- Math Amateur
- Thread
- Replies: 2
- Forum: Topology and Analysis
-
A
Green's theorem with a scalar function
Greetings! My question is: is it possible to use the green theorem to compute the circulation while in presence of a scalar function ? I know how to solve by parametrising each part but just in case we can go faster? thank you!- Amaelle
- Thread
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

MHB Understanding Bayes Theorem with an Example: 0.72 or 0.28?
https://lh4.googleusercontent.com/FCqUErWAqlG8w0CskhcsLgpG91xyxzAkV_nD-bZAq8147-_RKesQDpglwqF5ylKZ0Q6VW88jX-KNuIpSXi9vhw5AiWmwiv_fMyyUo_WWZJG4uwWS0aB-3rGMA0h0PDo7ZpolexCe this is the question Here is a tutorial video but his steps are very confusing to me. I personally know bayes theorem and...- shivajikobardan
- Thread
-
- Tags
- Bayes theorem Example Theorem
- Replies: 0
- Forum: Programming and Computer Science
-
T
A Noether's theorem time invariance -- mean value theorem use?
how does the first step use mean value theorem? I don't get it , can anyone explain , thanks. -

Use binomial theorem to find the complex number
This is also pretty easy, ##z^5=(a+bi)^5## ##(a+bi)^5= a^5+\dfrac {5a^4bi}{1!}+\dfrac {20a^3(bi)^2}{2!}+\dfrac {60a^2(bi)^3}{3!}+\dfrac {120a(bi)^4}{4!}+\dfrac {120(bi)^5}{5!}## ##(a+bi)^5=a^5+5a^4bi-10a^3b^2-10a^2b^3i+5ab^4+b^5i## ##\bigl(\Re (z))=a^5-10a^3b^2+5ab^4## ##\bigl(\Im (z))=...- chwala
- Thread
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
I Frontiers in Physics had 2 papers quest. Bell's theorem, any othrs?
One is fr. worker at U. Karlsruhe, another fr. Israeli res. The latter argued findings can be integrated into classical physics.- ndvcxk123
- Thread
- Replies: 2
- Forum: Quantum Physics
-

Solve the equation involving binomial theorem
$$(7-6x)^3+(7+6x)^3=1736$$ $$⇒(7^3(1-\frac {6}{7}x)^3+(7^3(1+\frac {6}{7}x)^3=1736$$ $$343[1-\frac {18}{7}x+\frac {216}{98}x^2-\frac{1296}{2058}x^3]+343[1+\frac {18}{7}x+\frac {216}{98}x^2+\frac{1296}{2058}x^3]=1736$$ $$343[2+\frac {432}{98}x^2]=1736$$ $$686+\frac {148,176}{98}x^2=1736$$ $$\frac...- chwala
- Thread
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
M
Dynamic Systems: Poincaré-Bendixson Theorem finite # of equilibria
Homework Statement:: Can someone explain the finite number of equilibria outcome of the Poincaré-Bendixson Theorem? Relevant Equations:: Poincaré-Bendixson Theorem [Mentor Note -- General question moved from the schoolwork forums to the technical math forums] Hi, I was reading notes in...- Master1022
- Thread
- Replies: 4
- Forum: Differential Equations
-
S
I Is this statement an aspect of the Hairy Ball or Fixed Point Theorem?
“Given any class of mutually exclusive classes, of which none is null, there is at least one class which has exactly one term in common with each of the given classes…” The reason this statement sounds like one of those theora is that I recall reading a Time-Life book on Mathematics, and there...- swampwiz
- Thread
-
- Tags
- Ball Fixed point Point Theorem
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
D
I Liouville's Theorem and Poincare Recurrence Theorem
Hi. I am working through some notes on the above 2 theorems. Liouville's Theorem states that the volume of a region of phase space is constant along Hamiltonian flows so i assume this means dV/dt = 0 In the notes on the Poincare Recurrence Theorem it states that if V(t) is the volume of phase...- dyn
- Thread
-
- Tags
- Poincare Recurrence Theorem
- Replies: 3
- Forum: Mechanics
-

Virial Theorem for an expanding globular cluster
I attached a file which shows my attempt to resolve this problem with the possible two pair interaction which gives us the kinetic energy of the cluster in an expanding system, at least I think so. But to be honest I´m more or less completely stuck with this question and I would be glad if...- Barbequeman
- Thread
- Replies: 3
- Forum: Introductory Physics Homework Help
-

B Question in the momemtum-impulse theorem derivation
when the net force is constant then Q1. rate of change of momentum (dp/dt) is zero or constant Q2. assuming dp/dt is constant we replaced it with ----> p2-p1(total change in momentum ) ? how?- just NOTHING
- Thread
- Replies: 9
- Forum: Mechanics
-

B I want this short proof of the Bolzano-Weierstrass Theorem checked please
Let ##X## be a bounded subset of ##\mathbb{R}## with infinite cardinality. We consider a countably-infinite subset of ##X##. We write this set as a sequence to be denoted ##\{a_n\}_{n\in\mathbb{N}}##. Now define ##A## to be the set of points in the sequence with the property that for each...- Eclair_de_XII
- Thread
- Replies: 8
- Forum: Calculus
-

B Proving half of the Heine-Borel theorem
Let ##X## be a closed and bounded subset of the real numbers. Let ##\{x_i\}_{i\in I}##, for some index ##I##, represent the set of limit points of ##X##. Since ##X## is closed, it must follow that ##\{x_i\}_{i\in I}\subset X##. Hence, the set of limit points must be bounded. Let ##\{U_j\}_{j\in...- Eclair_de_XII
- Thread
-
- Tags
- Theorem
- Replies: 3
- Forum: Calculus
-
R
I have a real simple question about the Pythagoras theorem
Here is the link. https://www.grc.nasa.gov/www/BGH/sincos.html Sorry just a little rusty on Pythagoras theorem. I mean the formula still holds but in order to find the opposite and the adjacent the opposite becomes the adjacent and vice versa .- rgtr
- Thread
-
- Tags
- Pythagoras Theorem
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
A
Engineering Is my method of solving this correct? Superposition theorem
Hello! Consider this circuit Now I want to calculate the current Ik. The values are given as follows; Uq1 = 12 V Uq2 = 18V R1 = R2 = 8 Ohm R3 = R4 = 20 Ohm My approach was using the Superposition theorem. First I deactived Uq2 and left Uq1 active. Now if I am not mistaken the resistors R2 R3...- arhzz
- Thread
- Replies: 15
- Forum: Engineering and Comp Sci Homework Help
-

I Darboux theorem for symplectic manifold
Hi, I am missing the point about the application of Darboux theorem to symplectic manifold case as explained here Darboux Theorem. We start from a symplectic manifold of even dimension ##n=2m## with a symplectic differential 2-form ##w## defined on it. Since by definition the symplectic 2-form...- cianfa72
- Thread
- Replies: 4
- Forum: Differential Geometry
-
K
A Uncertainties on Bayes' theorem
Hello! I have a setup consisting of some charged particles each of which is produced at a different position, ##(x_i,y_i,z_i)##. I don't know the exact position, but I know that each of the 3 variables is normally distributed with mean zero and standard deviation of 3 mm. What I measure in the...- kelly0303
- Thread
-
- Tags
- Theorem Uncertainties
- Replies: 19
- Forum: Set Theory, Logic, Probability, Statistics
-

I [Congruence class] Proof of modular arithmetic theorem
Could someone explain why ##[a][x_0]=[c]\iff ax_0\equiv c\, (mod\, m)##? My instructor said it came from the definition of congruence class. But I am not convinced.- Leo Liu
- Thread
-
- Tags
- Arithmetic Class Proof Theorem
- Replies: 2
- Forum: General Math
-
M
A Energy, mass and Noether’s theorem
Mentors note: split from https://www.physicsforums.com/threads/energy-mass-equivalence.1003564/ How do you measure energy?- md2perpe
- Thread
- Replies: 74
- Forum: Special and General Relativity
-
D
Use Liouville's theorem to show that two functions are equal
##lim_{|z|\rightarrow \infty}\frac{f}{g}=1\neq \frac{\infty}{\infty}## so ##lim_{|z|\rightarrow \infty}f\neq \infty## and ##lim_{|z|\rightarrow \infty}g\neq \infty##. Because f(z) and g(z) are bounded and entire, f(z) and g(z) are constant functions by Liouville's theorem . f(z) and g(z) are...- docnet
- Thread
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

Impulse-momentum theorem problem
The solution is from ##fdt=d(mv)=mdv+vdm## and separate the variables and then integrate them. But at first I tried this method. At time ##t##, suppose the mass of the cart is ##m##, and its velocity is ##v##. And suppose at time ##t+dt##, its mass will be ##m-\rho dt##, and its velocity...- Haorong Wu
- Thread
-
- Tags
- Theorem
- Replies: 14
- Forum: Introductory Physics Homework Help
-

Python Python’s Sympy Module and the Cayley-Hamilton Theorem
Continue reading...- Mark44
- Thread
- Replies: 1
- Forum: Programming and Computer Science
-
K
A Matrix proof of Euler's theorem of rotation
The question arises the way Goldstein proves Euler theorem (3rd Ed pg 150-156 ) which says: " In three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point"... -
F
A To understand the Darboux theorem
Darboux theorem says a derivative function must have an intermediate value theorem without requiring the derivative function to be continuous. Why is this property not true for any continuous function in its intermediate value theorem? -
M
I Bayesian Stats: Resources about Mercer's Theorem for Gaussian Processes
Hi, Question(s): 1. Are there any good resources that explain, at a very simple level, how Mercer's theorem is related to valid covariance functions for gaussian processes? (or would anyone be willing to explain it?) 2. What is the intuition behind this condition for valid covariance...- Master1022
- Thread
- Replies: 0
- Forum: Set Theory, Logic, Probability, Statistics
-
K
A A Question on a Wikipedia article on Bertrand's theorem
Wikipedia while deriving Bertrands theorem writes after some steps : However by a similar argument we can say that since ##β## is a constant then we can directly solve ##J^{\prime}(u)=1-\beta^{2}## and find that ##J=\left(1-β^{2}\right) u##) which is wrong. What went wrong? -
K
A Hooke's law, Bertrand's theorem and closed orbits
Bertrand's Theorem says : the only forces whose bounded orbits imply closed orbits are the Hooke's law and the attractive inverse square force. I'm looking at the hookes law ##f=-k r## and try to see explicitly that the orbit is indeed closed. I use the orbit equation ##\frac{d^{2} u}{d... -
Z
Possible to use work-energy theorem from a non-inertial frame?
In learning about translational and rotational motion, I solved a problem involving a wheel rolling down an inclined plane without slipping. There are multiple ways to solve this problem, but I want to focus on solutions using energy. Now to my questions. The reference frame in the posted...- zenterix
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-

I Stokes' theorem and surface integrals
Hi, So my goal is to compute the integral of the "curl" of the vector field ##A_i(x_i)## over a 2-dimensional surface. Following a physics book that I am reading, I introduce the antisymmetric 2-nd rank tensor ##\Omega_{ij}##, defined as: $$\Omega_{ij} = \frac {\partial A_i}{\partial x_j} -... -
K
Find the Conserved Quantity of a Lagrangian Using Noether's Theorem
So Noether's Theorem states that for any invarience that there is an associated conserved quantity being: $$ \frac {\partial L}{\partial \dot{Q}} \frac {\partial Q}{\partial s}$$ Let $$ X \to sx $$ $$\frac {\partial Q}{\partial s} = \frac {\partial X}{\partial s} = \frac {\partial...- koil_
- Thread
- Replies: 5
- Forum: Calculus and Beyond Homework Help