Another way to find trig identities

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

Using the identity's

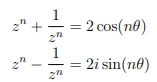
(1)

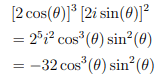
(2)

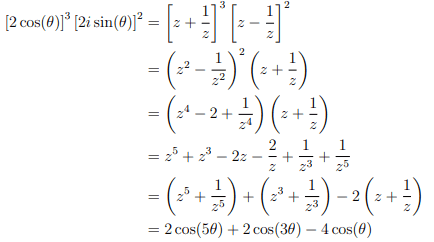
Gives,

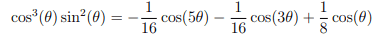
Why dose this elegant method work?

Many thanks!

 

[member 731016]

Sorry, I posted in the wrong forum. This was meant to be for the precalculus forum.

Many thanks!

 

[kuruman]

Are you asking about the connection between complex exponentials and sinusoidals? If so, you may find that this article addresses your question.

 

[Mark44]

Sorry, I posted in the wrong forum. This was meant to be for the precalculus forum.

Many thanks!

Thread locked. A related question is posted in the Precalc Homework section.