Benefits of time dilation / length contraction pairing?

[neopolitan]

Sure, that's just the standard meaning of what coordinate transformation equations are meant to do (although a coordinate transformation can also transform the intervals between an arbitrary pair of events in one frame to the intervals between the same pair of events in another frame).

Yes, as I said I'm fine with defining events in abstract notation rather than numerical values.

Then I can't understand why you said this:

These equations wouldn't "speak" about any event in particular, they relate the coordinates of any arbitrary event in one frame to the coordinates of the same event in the other frame, but either way it is necessary that you have a specific physical event in mind.

I took that to be criticism, although I couldn't understand what alternative you were presenting.

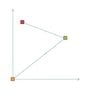
By the way, you talk about coordinates and intervals. To avoid having to do that, can we agree that coordinates are intervals (just a specific one where one of the implied pair is the origin of the axis)? I have no problem with the idea of rearranging my axes to transform any interval into a single coordinate, or the reverse.

On the image, we could call the red dot a coordinate, but it is also an interval from the orange dot to the red dot. Between the red dot and the green dot is an interval, but if I redefined my axes so that (0,0) was the red dot, then the green dot would be a coordinate from the red dot. I don't see a huge difference between coordinate and interval for this very reason.

cheers,

neopolitan

 

[JesseM]

I took that to be criticism, although I couldn't understand what alternative you were presenting.

It was less of a criticism and more of a puzzlement about your statement here:

I'm not worried that one pair might speaks about a YDE that is simultaneous in A's frame with A and B being colocated while the other speaks about a YDE that is simultaneous in B's frame with A and B being colocated. All I care about is whether the photon involved in each pair is the same photon, spawned by the same event.

You seemed to be saying that one pair would speak specifically speak about "a YDE that is simultaneous in A's frame with A and B being colocated", while the other pair would speak specifically about a YDE that was simultaneous with colocation in B's frame. But there's no specificity here, since each pair of equations is totally general, either pair could deal with either type of YDE. For example, one pair of equations for the Lorentz transform would be x'=gamma*(x-vt) and t'=gamma*(t-vx/c^2); if I knew the x,t coordinates of a YDE that was simultaneous with colocation in the unprimed A frame I could plug those in and get the same event's x',t' coordinates, and likewise if I knew the x,t coordinates of a YDE that was simultaneous with colocation in the primed B frame I could plug those in and get the same event's x',t' coordinates. Of course that's assuming I started out knowing the x,t coordinates of each type of event, I suppose in the case of a YDE that was simultaneous with colocation in the primed frame it's more plausible I would start out knowing the event's x',t' coordinates, so maybe that's what you meant (but then again events aren't 'native' to any particular coordinate system, it's possible I would focus on this particular event while working in unprimed coordinates for some other reason without knowing in advance it had the property of being simultaneous with colocation in the primed frame).

By the way, you talk about coordinates and intervals. To avoid having to do that, can we agree that coordinates are intervals (just a specific one where one of the implied pair is the origin of the axis)? I have no problem with the idea of rearranging my axes to transform any interval into a single coordinate, or the reverse.

Sure, that's a good way of thinking about it.

 

[neopolitan]

I'm going to try to address the x' = x - vt thing.

Rather than go over each of your paragraphs, I will try to just explain it. I hope this will satisfy you.

The implication with x' = x - vt is that you have an unprimed observer who is considering what things would be like for someone else who is moving with a speed of v towards a location, or event, at a distance of x away.

At a time t, x will be unchanged for our unprimed observer in the unprimed frame. However, the separation between the someone else and that location, or the location where the event took (or will take or takes) place, will have changed.

Our unprimed observer can then work out that at t this equation applies:

x' = x - vt

or to be more specific, since we are describing a function of time,

x'(t) = x - vt

This equation can be used to obtain the spatial interval between the someone else and any event that happens at any time at any location under Galilean relativity.

In Galilean relativity, that interval is also the spatial coordinate for the event in the someone else frame.

Can you see that while you are 100% right about x'(t) = x - vt applying to spatial coordinates, that that is not 100% of the story?

cheers,

neopolitan

 

[neopolitan]

You seemed to be saying that one pair would speak specifically speak about "a YDE that is simultaneous in A's frame with A and B being colocated", while the other pair would speak specifically about a YDE that was simultaneous with colocation in B's frame. But there's no specificity here, since each pair of equations is totally general, either pair could deal with either type of YDE. For example, one pair of equations for the Lorentz transform would be x'=gamma*(x-vt) and t'=gamma*(t-vx/c^2); if I knew the x,t coordinates of a YDE that was simultaneous with colocation in the unprimed A frame I could plug those in and get the same event's x',t' coordinates, and likewise if I knew the x,t coordinates of a YDE that was simultaneous with colocation in the primed B frame I could plug those in and get the same event's x',t' coordinates.

$$x' = \gamma. (x - vt)$$
$$t' = \gamma. (t - vx/c^2)$$

$$x = \gamma. (x' + vt')$$
$$t = \gamma. (t' + vx'/c^2)$$

gamma = 1.25
v = 0.6c
event (x,t) = (10,0)

x' = 12.5
t' = - 7.5

This event was not simultaneous with t' = 0

But we can plug these right back into the second pair of equations and get the original x and t back out.

Alternatively, we could start with

event (x',t') = (10,0)

which is a totally different event, just one which is simultaneous (in the primed frame) with t' = 0 - and we can do the same sorts of substitutions.

Notionally, we could start with an event which is not simultaneous with either.

I'm not that fussed. It's just much simpler to start with an event that is simultaneous with the colocation of the origins of the axes and work from there.

What I do know is that no matter what event you start from, that event can be associated with a photon which could result in two more events (such as: photon colocated with A and photon colocated with B).

Am I making any sort of headway?

cheers,

neopolitan

 

[JesseM]

I'm going to try to address the x' = x - vt thing.

Rather than go over each of your paragraphs, I will try to just explain it. I hope this will satisfy you.

The implication with x' = x - vt is that you have an unprimed observer who is considering what things would be like for someone else who is moving with a speed of v towards a location, or event, at a distance of x away.

At a time t, x will be unchanged for our unprimed observer in the unprimed frame. However, the separation between the someone else and that location, or the location where the event took (or will take or takes) place, will have changed.

Our primed observer can then work out that at t this equation applies:

x' = x - vt

or to be more specific, since we are describing a function of time,

x'(t) = x - vt

So was I right in guessing that you are using x'(t) to refer to the distance in the unprimed frame between the primed observer and the location, despite the fact that the symbol is primed? If so, why do you say "our primed observer" works out this equation, if all of the terms are defined in terms of the unprimed frame? And if this is what you mean, can you see why this notation might be extremely confusing, especially since you said that the high school student was aware of this equation because he paid attention in class, and yet in any textbook which used standard notation conventions the meaning of this equation would always be in the context of the Galilei transformation relating one frame to another? If you're going to take standard textbook equations and change the meaning of the terms this is really something you need to explain in advance to avoid confusion.

This equation can be used to obtain the spatial interval between the someone else and any event that happens at any time at any location under Galilean relativity.

But it has nothing specifically to do with Galilean relativity, since if x'(t) just means the distance in the unprimed frame between B and the location at x, then the equation x'(t)=x-vt isn't even relating multiple frames, it would be equally valid in SR.

In Galilean relativity, that interval is also the spatial coordinate for the event in the someone else frame.

Yes.

Can you see that while you are 100% right about x'(t) = x - vt applying to spatial coordinate, that that is not 100% of the story?

Not really sure what you mean by "applying to spatial coordinate". Do you just mean that x'=x-vt normally is understood to relate one Galilean frame's coordinates to another's, but that we can in principle redefine the meaning of x' so that it refers to the spatial separation between a moving object and a fixed location x in a single frame? If so I agree (and I already asked you if you were making such a redefinition in several earlier posts). But when you change the physical definition of the terms you're dealing with a different physical equation even if the symbols are the same, so it's not like there are two different ways of looking at the same physical equation. What's more, writing a new physical equation using notation that has a different preexisting established meaning is kind of perverse from a pedagogical point of view (sort of like if I wrote the equation E=mc^2 and said that E stands for force and c stands for the square root of acceleration), there's already an accepted convention about the physical interpretation of primed vs. unprimed coordinates and about the equation x'=x-vt, if you want to write down an equation giving a spatial separation in the unprimed frame then it would be much better to use some different notation which wouldn't be so likely to confuse people who were trying to understand you, like s(t) = x_a - vt.

 

[JesseM]

$$x' = \gamma. (x - vt)$$
$$t' = \gamma. (t - vx/c^2)$$

$$x = \gamma. (x' + vt')$$
$$t = \gamma. (t' + vx'/c^2)$$

gamma = 1.25
v = 0.6c
event (x,t) = (10,0)

x' = 12.5
t' = - 7.5

This event was not simultaneous with t' = 0

But we can plug these right back into the second pair of equations and get the original x and t back out.

Right, that was exactly my point. Neither pair of equations deals specifically with this event as your earlier comment sounded like it was saying, we could either start with the event's x and t coordinates and use the first pair of equations to get its x' and t' coordinates, or we could start with the event's x' and t' coordinates and use the second pair of equations to get its x and t coordinates. It may be a little more "natural" to start with the coordinate system where the time coordinate is zero, so that's probably what you meant in that earlier comment. In any case I don't really think we have any remaining disagreement here.

 

[neopolitan]

So was I right in guessing that you are using x'(t) to refer to the distance in the unprimed frame between the primed observer and the location, despite the fact that the symbol is primed? If so, why do you say "our primed observer" works out this equation, if all of the terms are defined in terms of the unprimed frame?

Thankfully I only ever mentioned one observer, so it should be obvious that this was a typo. Note I mentioned "observer" and "someone else". Wherever observer was written it should have been prefixed with unprimed. Sorry.

With that fixed (I edited the post) can you revisit your questions and see if they still apply.

thanks,

neopolitan

Oh, and by the way, I never primed a frame. That assumption on your part might be confusing you. Remember my description of x'_{a[\sub] from an earlier post?}

 

[JesseM]

Thankfully I only ever mentioned one observer, so it should be obvious that this was a typo. Note I mentioned "observer" and "someone else". Wherever observer was written it should have been prefixed with unprimed. Sorry.

With that fixed (I edited the post) can you revisit your questions and see if they still apply.

Yes, aside from that one sentence about the primed observer all my other points still apply; I still think it's extremely perverse from a pedagogical point of view to take an equation with an established meaning like x'=x-vt and redefine the meaning of the terms so it the equation's physical meaning becomes completely different (without stating explicitly that this is what you're doing), and to say that a high school student is aware of this equation from his classes without mentioning that his interpretation of the symbols has nothing to do with what he actually would have been taught in class. Do you not see how ridiculously confusing this is for readers? Again, if you want to write an equation expressing only the displacement in the unprimed frame, write something like d(t) = x_a - vt.

Oh, and by the way, I never primed a frame.

It doesn't matter if you did, what matters is that the equation x'=x-vt, whenever it appears in any physics textbook, always appears in the context of the Galilei transform where it relates coordinates in an unprimed frame to coordinates in a primed frame. And you said that the high school student was aware of this equation from his classes (presumably not taught by a teacher who was making up his own idiosyncratic notation), not to mention you even said that you were starting your derivation from a "Galilean" perspective! Like I said, this is akin to writing the equation E=mc^2 without mentioning that you've mentally redefined E to mean force and c^2 to mean acceleration.

 

[neopolitan]

So, what you are saying is that I am using an equation which looks a lot like the Galilean boost, but isn't, using a process which you may not understand, and arriving at a equations which look a lot like the Lorentz Transforms but are not?

This is a rhetorical question, and I am taking the answer to be yes.

So, I've found a new set of equations. I am so proud. I hereby name them "the Neopolitonian boost" and "the Neopolitonian Transforms".

The Neopolitonian boost

This equation is used in a scenario where there are two observers (A and B) and an Event.

According to A that Event is at (x_a,0). A photon from that event reaches A at event (0,t_a)

According to A, B has a velocity of v towards the Event and the boost is used to find the interval between B and that Event (according to A) at t_a

x'_a = x_a - v.t_a

(In our numerical example, this is 5 = 8 - 0.6 * 5 )

The Neopolitonian Transform

This pair of equations is used to transform coordinates between two inertial observers (or two inertial frames). For example, in the scenario above, all the values given are according to A. The Neopolitonian Transform gives a value of x' and t' according to B (x'_b and t'_b) - which make B's frame the primed frame. This can also be called "A looking at B" since the values of x'_b and t'_b are given in terms of x_a and t_a, ie "what do B's values look like in terms of A's values?"

x'_b = $$\gamma$$.(x_a - v.t_a)

t'_b = $$\gamma$$.(t_a - v.x_a/c²)



Ok. Are you happy to talk about the process used to derive the Neopolitonian Transform from the Neopolitonian boost?

Plus, are you absolutely certain that no-one is going to accuse me of just rebadging the Galilean boost and the Lorentz Transform, because it is sooooo obvious that they are not the same as the Neopolitonian boost and the Neopolitonian Transform?

cheers,

neopolitan

PS I want make explicit the fact that I still remember that we can convert coordinates to intervals and back again. I also know that it is applicable in the above.

 

[JesseM]

So, what you are saying is that I am using an equation which looks a lot like the Galilean boost, but isn't, using a process which you may not understand, and arriving at a equations which look a lot like the Lorentz Transforms but are not?

I was mainly expressing frustration that you don't seem to consider how your idiosyncratic way of explaining yourself will lead naturally to some obvious misunderstandings which have to be laboriously worked out over a long series of subsequent posts, which could have been easily avoided if you explained the difference between your equations and the "standard" ones to begin with, or made your notation different from that of standard equations so such misunderstandings would be less likely to occur. Now I understand what you meant by x'=x-vt in post 295, but a lot of wasted time could have been avoided if you had been more explicit about the way you were redefining things at the start. If you got confused by someone's explanation of a series of equations which included the equation E=mc^2, and only after a long discussion did he make clear that he was defining E to mean force and c to mean the square root of acceleration, wouldn't you find this a little frustrating too?

So, I've found a new set of equations. I am so proud. I hereby name them "the Neopolitonian boost" and "the Neopolitonian Transforms".

The Neopolitonian boost

This equation is used in a scenario where there are two observers (A and B) and an Event.

According to A that Event is at (x_a,0). A photon from that event reaches A at event (0,t_a)

According to A, B has a velocity of v towards the Event and the boost is used to find the interval between B and that Event (according to A) at t_a

x'_a = x_a - v.t_a

(In our numerical example, this is 5 = 8 - 0.6 * 5 )

It isn't really proper to use the term "boost" here, as the word "boost" in physics refers to a transformation between two frames (for example see the last paragraph in this section of wikipedia's Lorentz transformation article). Your equation is just a simple kinematical equation for the separation between an object moving at constant coordinate speed and another object at fixed coordinate position, it would hold in absolutely any coordinate system whatsoever (like an inertial SR frame or even a non-inertial frame) and therefore has no specific relation to anything "Galilean".

The Neopolitonian Transform

This pair of equations is used to transform coordinates between two inertial observers (or two inertial frames). For example, in the scenario above, all the values given are according to A. The Neopolitonian Transform gives a value of x' and t' according to B (x'_b and t'_b) - which make B's frame the primed frame. This can also be called "A looking at B" since the values of x'_b and t'_b are given in terms of x_a and t_a, ie "what do B's values look like in terms of A's values?"

x'_b = $$\gamma$$.(x_a - v.t_a)

t'_b = $$\gamma$$.(t_a - v.x_a/c²)

Why do you call this the "Neopolitan transform"? If it really holds for events at arbitrary coordinates in the A frame, and gives you the corresponding coordinates of the same event in the B frame, then it obviously has the same physical meaning as the Lorentz transformation, unlike your equation x'_a = x_a - v.t_a which did not have the same physical meaning as the Galilei transformation equation x' = x - vt since you were not relating the coordinates of two different frames. I'm trying to get you to communicate your ideas in a non-confusing way which avoids hours of back-and-forth posts clarifying your meaning which could have been easily avoided if you had stated things more clearly at that outset--in order to do this, you need to think carefully about the physical meaning of the equations you write in relation to the physical meaning of standard textbook equations, and if you realize your equation has a different physical meaning in spite of superficial similarities to an existing equation then don't write it in exactly the same form without pointing out the difference, but likewise if your equations do have the same physical meaning as existing equations then you should be clear on this and not talk as though the equation is original to you just because you've altered the notation slightly. This issue of your not thinking through the physical meaning of equations is one that seems to come up again and again in our discussions--it arose in our discussions of the difference between the time dilation equation and the "temporal analogue for length contraction" too--so if you don't really follow the point I'm making (as suggested by your indiscriminately renaming equations above regardless of whether they do or don't have the same physical meaning as existing equations) then I'd like to try to focus on this until you understand.

But as a sort of aside to this, although the words you use to describe the equations above indicate they have the same physical meaning as the Lorentz transformation, I am in fact skeptical that your actual derivation would in fact prove something as general as the words suggest, unless you have totally changed the proof from what you offered before. I expressed my view of the physical meaning of the equations you had derived back in post 247--as far as I could tell, your derivation only proved that x'_a would equal gamma*(x_b + vt_b) in the specific case where x'_a was defined as the interval between E_a and the light passing B, while x_b and t_b were the intervals between a different pair of events, namely the event of E_b and the event of the light passing A. As I explained in those diagrams, by exploiting the symmetry of your scenario we can see that all the intervals between the first pair of events are identical to the intervals between the second pair, explaining why your equation comes out looking just like the Lorentz transformation even though it's not dealing with a single pair of events like the Lorentz transformation, but it seemed to me we only know about this symmetry because we already know how the two frames are related by the Lorentz transformation. In any case, even if we "allow" this symmetry to be exploited in the proof, the scope of the proof would still be limited to showing that the separation between events on the path of a light beam obey an equation like x'_a = gamma*(x_b + vt_b), the proof you presented simply wouldn't tell cover the case of pairs of events with a timelike or spacelike separation (though we know from other more general proofs that the equation would be the same). Finally, there was a step midway through the proof that didn't seem justified to me, where you said that we could assume the factor in x'_A = (a factor times).x'_B was the same as the factor in x_B = (a factor times).x_A--I explained my objection to this at the very bottom of post 280, for example. Basically, unless you have made really large changes to the proof you already presented, it's unlikely that these criticisms will change.

Plus, are you absolutely certain that no-one is going to accuse me of just rebadging the Galilean boost and the Lorentz Transform, because it is sooooo obvious that they are not the same as the Neopolitonian boost and the Neopolitonian Transform?

I am certain that if you stated the physical meanings of the equations explicitly in the way you did above, anyone knowledgeable about physics could be convinced that the first equation does not have the same physical meaning as the Galilean boost (because it's an intrinsic part of the definition of the 'Galilean boost' x' = x - vt that it relates one frame to another, whereas you defined your equation to only involve the coordinates of a single frame), while the second set of equations does have the same physical meaning as the Lorentz transformation (as you defined the meaning of the second set of equations in words above, not saying anything about whether your derivation would actually prove those words). If there is any doubt in your mind about either of these points I suggest we focus on the issue of the physical meaning of the Galilean boost x'=x-vt and the Lorentz transformation equations and how it relates to the equations you wrote, and leave other issues for later.

 

[neopolitan]

I disagree with your analogy, but I understand your frustration.

Can we agree that it would be silly for me to claim that I have found a new equation which looks pretty much like the Lorentz Transform, and claim it as my own?

That leaves the method for getting there and the boost.

Did you see my PS in the previous post?

It was there specifically because I wanted you to remember that fact and know that I remember it.

In Galilean relativity, the (spatial) interval from B to an event is the coordinate of the event in B's rest frame.

Do we disagree about that?

If we can agree on that, then I think I could call x' = x - vt a (spatial) boost, and I think I would not get away with calling x'_a = x - vt_a the Neopolitonian (not neopolitan) boost. It would swiftly be recognised as a slight rewording of the Galilean (spatial) boost.

The thing that would distinguish it, possibly is the implication that if it is just a slight rewording of the Galilean boost ie

x'_a = x - vt_a

then

t'_a = t_a - NOTE, I am not saying this, this is the second part of an if-then statement

It is something that I go on to disprove. But until this second part is disproved, I would consider it to be the Galilean boost.

cheers,

neopolitan

 

[JesseM]

In Galilean relativity, the (spatial) interval from B to an event is the coordinate of the event in B's rest frame.

Do we disagree about that?

They happen to be equal, but an equation telling you about the spatial interval has a different physical meaning than an equation telling you about the coordinate in B's rest frame. In a given physics equation every symbol must have a single well-defined meaning.

If we can agree on that, then I think I could call x' = x - vt a (spatial) boost

Not if you have defined x' to mean the spatial interval in A's frame. You may have outside knowledge that the spatial interval in A's frame is equal to the coordinate in B's frame, but the equation itself, with the symbols defined in this way, doesn't tell you anything about B's frame.

and I think I would not get away with calling x'_a = x - vt_a the Neopolitonian (not neopolitan) boost. It would swiftly be recognised as a slight rewording of the Galilean (spatial) boost.

No, it wouldn't be a "boost" at all because it only deals with one frame. If we define x'_a as merely the coordinate separation between an object at position x and an object B moving towards x at coordinate speed v (which started at x=0 at t=0), all in A's coordinate system, do you agree that this is a purely kinematical equation which is independent of the laws of physics, or of what type of coordinate system you're using (inertial or non-inertial)?

Think of actually writing out the physical meaning of all the terms in any equations in words. One equation is:

(distance in A's frame between B and object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

This equation, again, would work in absolutely any type of coordinate system whatsoever. The second equation is different in that it only works when using Galilean inertial frames, and it can be written as:

(position in B's frame of object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

Of course, we also happen to know that in Galilean relativity the following is true:

(distance in A's frame between B and object at position x in A's frame at time t in A's frame) = (position in B's frame of object at position x in A's frame at time t in A's frame)

But this is knowledge external to the first two equations themselves. Think of physics equations as very stupid things that can only give you an answer to one specific type of question, and they have no knowledge of any larger context. The only way two equations can be considered "the same" is if they are answering exactly the same physical question, and only the notation is different.

It may also help to point out that someone could easily have "discovered" the first equation before the discovery of the Galilei transformation, since the first equation doesn't involve multiple coordinate systems. Do you think it would be fair for this person to demand that the Galilei transformation be renamed after themselves, since they had already discovered the equation even though the physical meaning of what was being calculated was different and they hadn't even been thinking about the relation between multiple frames?

 

[neopolitan]

While I applaud your dedication to rigour, I think you take it too far.

Just out of curiosity, I look http://www.fourmilab.ch/etexts/einstein/specrel/www/" and searched for the word "frame". It appears exactly once, in the introduction, in the phrase "frames of reference" in the context of describing the first postulate.

While trying not to go so far as committing an "appeal to authority", I do want to know why I am being held to such high standards of rigour (specifying that the Galilean boost addresses a single question about frames) when the genius who came up with Special Relativity in his own way didn't really mention frames at all?

I'm not saying you are wrong that the Galilean boost is about frames, and the Lorentz Transformation is about frames, I am just wondering if your demands are truly warranted.

They happen to be equal, but an equation telling you about the spatial interval has a different physical meaning than an equation telling you about the coordinate in B's rest frame. In a given physics equation every symbol must have a single well-defined meaning.

Would you be happy if there was an extra step added in which I address Galilean frames, say the equation is x' = x - vt and that there is also a kinematic equation x' = x - vt and while they talk about different things, the relationship x' = x - vt holds equally for whatever values of x and t you enter into it? (Since the conditions under which the equation holds are the same for x' = x - vt and for x' = x - vt).

Not if you have defined x' to mean the spatial interval in A's frame. You may have outside knowledge that the spatial interval in A's frame is equal to the coordinate in B's frame, but the equation itself, with the symbols defined in this way, doesn't tell you anything about B's frame.

Addressed above.

No, it wouldn't be a "boost" at all because it only deals with one frame. If we define x'_a as merely the coordinate separation between an object at position x and an object B moving towards x at coordinate speed v (which started at x=0 at t=0), all in A's coordinate system, do you agree that this is a purely kinematical equation which is independent of the laws of physics, or of what type of coordinate system you're using (inertial or non-inertial)?

Addressed above.

It may also help to point out that someone could easily have "discovered" the first equation before the discovery of the Galilei transformation, since the first equation doesn't involve multiple coordinate systems. Do you think it would be fair for this person to demand that the Galilei transformation be renamed after themselves, since they had already discovered the equation even though the physical meaning of what was being calculated was different and they hadn't even been thinking about the relation between multiple frames?

No, and my suggestion to rename equations was entirely facetious.

However, since we know that the interval between B and an event is the same in both frames, and that interval is the coordinate in the B frame, then I fail to see why I can't use the equation the way I do.

I do wonder if you have the visual ability to see that what I am doing is not really invalid.

I point you back to the idea that we can shift the origins of our axes (within the relevant frame, of course) for convenience. We do that anyway, by making the interval between an observer and an event parallel to the x-axis. While it is entirely sensible to place the origin of the x-axis where our reference point is (nominally an observer), the point is that this is an arbitrary decision - arbitrary but sensible.

In short, are you happy with:

Introduce Galilean frames (hopefully already done by the education system)
Introduce a kinematic equation in the form x' = x - vt (partially done)
Point out that both equations operate on the same conditions
Go from there into the derivation of Lorentz equations

cheers,

neopolitan

PS Am I going to have to draw another diagram? I've already been thinking of the best way to try to show you that what I am doing is not as whacky as you seem to think it is. Part of the problem might be that I am an engineer, manipulating equations is partly what I do. As someone with more of a physics bent, you don't seem to like the actual use of equations (or what you might term "abuse of equations" )

 

[sylas]

While I applaud your dedication to rigour, I think you take it too far.

With respect, I don't think so. I think you need to be more rigorous and careful in your definitions. This is not an excessive hurdle, and it's getting better; but I think you need to keep being as rigourous as you can manage. The comparison with Einstein is invalid. Being rigourous does not mean "mentioning frames". It means being unambiguous and precise in whatever terminology or diagrams you use. It's not that you need full derivations and proofs of everything; just less ambiguity.

No offense intended... but I've been watching with some interest and I think the major problem is a lack of precision and rigour, and it should not be that hard to fix.

Cheers -- sylas

 

[neopolitan]

With respect, I don't think so. I think you need to be more rigorous and careful in your definitions. This is not an excessive hurdle, and it's getting better; but I think you need to keep being as rigourous as you can manage. The comparison with Einstein is invalid. Being rigourous does not mean "mentioning frames". It means being unambiguous and precise in whatever terminology or diagrams you use. It's not that you need full derivations and proofs of everything; just less ambiguity.

No offense intended... but I've been watching with some interest and I think the major problem is a lack of precision and rigour, and it should not be that hard to fix.

Cheers -- sylas

Thanks, it helps to get another perspective.

 

[JesseM]

While I applaud your dedication to rigour, I think you take it too far.

Just out of curiosity, I look http://www.fourmilab.ch/etexts/einstein/specrel/www/" and searched for the word "frame". It appears exactly once, in the introduction, in the phrase "frames of reference" in the context of describing the first postulate.

The entire paper is about what we now call frames, Einstein just doesn't use that term. When he introduces a "a system of co-ordinates in which the equations of Newtonian mechanics hold good" at the beginning of section 1, what do you think that is if not an inertial frame? And he talks about different systems of coordinates throughout the paper, sometimes just using the word "system" (it's clear he means coordinate system and not some other type of physical system from the context)--for example, part 3, where he actually derives the Lorentz transformation, is titled "Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former".

While trying not to go so far as committing an "appeal to authority", I do want to know why I am being held to such high standards of rigour (specifying that the Galilean boost addresses a single question about frames) when the genius who came up with Special Relativity in his own way didn't really mention frames at all?

Again, the whole paper is about frames. The precise word is irrelevant as long as the concept is understood; I'd be equally happy with saying the Galilean boost is about relating the coordinates of an event in one "system of coordinates" to the coordinates of the same event in another "system". Whatever wording you use, this is conceptually quite different from just telling you how the coordinate separation between two objects is changing in a single coordinate system.

I'm not saying you are wrong that the Galilean boost is about frames, and the Lorentz Transformation is about frames, I am just wondering if your demands are truly warranted.

Just the fact that I was confused for so long by the meaning of the equation x' = x - vt in post 295 shows that they are warranted; I'd rather not get into more lengthy discussions over such trivial stuff in the future. Even if you incorrectly described the equation as the Galilean boost, the problem could have been avoided if you had spelled out in words what each symbol meant physically; if you had said at the outset that x' was supposed to represent a separation in the same frame that x and t referred to, then I might have offered a quick correction about terminology but there wouldn't have been all the confusion about what you were trying to demonstrate with your equations. But the combination of not giving physical definitions of your symbols at the outset, using the term "Galilean boost", and writing your equation using exactly the same notation as is usually used for the Galilean boost naturally led me to draw the wrong conclusions about the physical meaning of the equation. Hopefully you agree that, spelled out in words, this:

(position in B's frame of object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

...is telling us something physically from this?

(distance in A's frame between B and object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

Would you be happy if there was an extra step added in which I address Galilean frames, say the equation is x' = x - vt and that there is also a kinematic equation x' = x - vt and while they talk about different things, the relationship x' = x - vt holds equally for whatever values of x and t you enter into it? (Since the conditions under which the equation holds are the same for x' = x - vt and for x' = x - vt).

As long as you define the physical meaning of whatever equations you use I'll be OK, although from a pedagogical point of view I don't really like the approach of using identical notation for two physically different equations. In any case, is it necessary to discuss Galilean relativity at all in your derivation? Isn't the kinematical equation the only one you actually make use of?

It may also help to point out that someone could easily have "discovered" the first equation before the discovery of the Galilei transformation, since the first equation doesn't involve multiple coordinate systems. Do you think it would be fair for this person to demand that the Galilei transformation be renamed after themselves, since they had already discovered the equation even though the physical meaning of what was being calculated was different and they hadn't even been thinking about the relation between multiple frames?

No, and my suggestion to rename equations was entirely facetious.

I understood it was meant to be facetious...but my point in the above comment was, if you agree this hypothetical pre-Galileo guy shouldn't get credit for the Galilei transformation despite writing down an equation like x' = x - vt, doesn't that mean you should also agree we shouldn't use the same terminology for his kinematical equation that we do for the spatial component of the Galilei transformation, even if they look the same symbolically?

I do wonder if you have the visual ability to see that what I am doing is not really invalid.

It has nothing to do with visual abilities, I get visually why it works out that the separation in A's frame between B and the object at position x is always going to be equal to the position coordinate assigned to that object in B's frame. The point is that the equations are telling you different things physically, and that since I naturally thought you were introducing x'=x-vt in post 295 to transform into B's frame, I was confused since under the Galilei transformation the light could not be moving at c in B's frame.

In short, are you happy with:

Introduce Galilean frames (hopefully already done by the education system)
Introduce a kinematic equation in the form x' = x - vt (partially done)

As I said I don't like using the same notation for two equations with different physical meanings, and I think from a pedagogical point of view it's more confusing than helpful.

Point out that both equations operate on the same conditions

By "operate on the same conditions", I take it you mean if we pick a given x,t in A's frame, we get the same value for the answer? That's fine as long as you point out the physical meaning of the "answer" is different.

PS Am I going to have to draw another diagram? I've already been thinking of the best way to try to show you that what I am doing is not as whacky as you seem to think it is. Part of the problem might be that I am an engineer, manipulating equations is partly what I do. As someone with more of a physics bent, you don't seem to like the actual use of equations (or what you might term "abuse of equations" )

Now that I understand the physical meaning of your symbols I don't object to "what you are doing" in the derivation so far, only to how you are explaining it. And I have no dislike of equations (a scurrilous charge for a student of physics, my good sir! ), I just need to be clear on the physical meaning of any variables/constants that appear in them.

 

[neopolitan]

I am happy to use the kinematic equation from the start. Historically, how long ago was that equation (or at least that relationship) first identified? (Part of my interest is to see how long ago we could have got to SR. If the kinematic equation is all that is required, rather than Galilean relativity, that might actually push the possible date back to before the 1100's given an early Islamic mathematician's work. "In dynamics and kinematics, Biruni was the first to realize that acceleration is connected with non-uniform motion, which is part of Newton's second law of motion." - http://en.wikipedia.org/wiki/Al-Biruni" Sadly, the coverage of this fellow's work is less visible to me than that for da Vinci, Galileo and Newton, but it seems to me that if Al-Biruni got so far as to consider non-uniform motion then uniform motion was probably understood. Al-Biruni's contribution to optics as claimed in the same article is interesting as well, apparently being among the first to consider the speed of light to be finite (but faster than sound) - it makes one wonder why someone like this has been pretty much invisible. There is what seems to be an inconsistency in that article, did people prior to Al-Biruni think that the speed of sound was infinite along with the speed of light? {Since Al-Biruni is credited with not only being among to consider the speed of light to be finite, but also the first to find that the speed of light is much faster than the speed of sound. I would have thought that infinitely fast is much faster than the speed of sound.} But this is merely an aside.)

Amusingly, I did try something like your:

(position in B's frame of object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

but with subscripts. I found it too unwieldy and distracting. So, I do see the value in it.

Anyway, since with the riders, you don't object with my derivation so far, perhaps I should try to sum up where we are right now, before we go further. If I do that, being as rigorous as I can, are you happy to work from that point onwards?

cheers,

neopolitan

 

[JesseM]

I am happy to use the kinematic equation from the start. Historically, how long ago was that equation (or at least that relationship) first identified?

Not sure, I guess as soon as people came up with the notion of measuring how distances between things change with time (which would require at least somewhat fine-grained clocks), along with the concept of speed as distance traveled/time elapsed, they could have realized that the distance between a thing moving at constant speed v and a stationary thing would be shrinking at v times the time elapsed. Maybe this would come up in seafaring or something, even if it wasn't written as an algebraic equation. On the other hand, to write an equation like x - vt for a distance between a moving object and a stationary one, you need some notion of assigning objects position coordinates on a coordinate grid (or at least a coordinate line), and of choosing your origin so the moving object starts at position x=0 at time t=0, don't know if people would have thought in those terms until Descartes invented Cartesian geometry (incidentally, Galileo was about thirty years older than Descartes so I'd guess he never actually wrote the 'Galilei transformation' in algebraic terms, even if it's implicit in his work that he was saying the laws of physics would be invariant under this transformation).

Amusingly, I did try something like your:

(position in B's frame of object at position x in A's frame at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

but with subscripts. I found it too unwieldy and distracting. So, I do see the value in it.

Yeah, it would be unwieldy to include the full description in the symbol itself, but it would be helpful if each time a new symbol is introduced, you could say something like "define x' as the position in B's frame of the event that had coordinates x,t in A's frame", something along those lines.

Anyway, since with the riders, you don't object with my derivation so far, perhaps I should try to sum up where we are right now, before we go further. If I do that, being as rigorous as I can, are you happy to work from that point onwards?

Sure, as long as being rigorous means defining the physical meaning of any new terms you introduce.

 

[neopolitan]

Can we use this notation?

x'_a = the separation (hence the x) between B and an Event (hence the prime) according to A (hence the _a)

This perhaps should be expanded a little to specify clearly that unprimed means "between A and an Event". And capitalisation of Event is used to clarify that I am referring to a specific event, not just any event.

So you have two frames (A -> Event and B -> Event), as many perspectives as you like (_a, _b, _c, _d - but we will only use two) and we will have two dimensions (x and t).

I might also need to clarify something that I have firmly in mind about my t values.

When we draw a spacetime diagram, we can draw an interval between, say, A and an Event in A's future. But in the real world (another engineering trait coming out perhaps), A will not know about that Event until enough time has elapsed for the Event to take place (in the A frame) and for a photon to travel from the Event to A.

For that reason, I see utility in moving the origin of the t_a axis to be simultaneous with the Event in the A frame. If I do that then, as a consequence, x_a = c.t_a.

Notionally, A and B are colocated at (0,0) - now this does not have to physically take place because we calculate intervals so any initial offset will cancel out.

Are you happy with this? Clarifying what I am asking:

1. Are you happy with the notation regime suggested?
2. Are you happy with the concept that A and B are notionally colocated at (0,0), but they don't actually have to be colocated at that time or place?

cheers,

neopolitan

 

[JesseM]

Can we use this notation?

If x'_a is meant to be a variable, as opposed to the separation between B and the Event at some specific time, can we write it as x'_a(t)?

I might also need to clarify something that I have firmly in mind about my t values.

When we draw a spacetime diagram, we can draw an interval between, say, A and an Event in A's future. But in the real world (another engineering trait coming out perhaps), A will not know about that Event until enough time has elapsed for the Event to take place (in the A frame) and for a photon to travel from the Event to A.

For that reason, I see utility in moving the origin of the t_a axis to be simultaneous with the Event in the A frame. If I do that then, as a consequence, x_a = c.t_a.

In other recent posts (such as 308) you used t_a to refer to a specific time interval (between A and B being colocated and the photon passing A) in A's frame, so it's potentially confusing to refer to "the t_a axis"--I assume you just mean the t-axis in A's frame? Whereas in the equation x_a = c.t_a, does t_a still refer to that time interval I mentioned? And when you talk about moving the origin to be "simultaneous with the Event in the A frame", do you just mean the origin has the same time coordinate as the Event (i.e. the t-coordinate of the Event in A's frame is 0), not that the Event is actually at the origin? So it's still true that the event has coordinates x=x_a, t=0 in A's frame, and it's still true that the photon reaches A at x=0, t=t_a? If so I don't really understand why you talk about "moving the origin", since this is exactly how things were before.

Notionally, A and B are colocated at (0,0) - now this does not have to physically take place because we calculate intervals so any initial offset will cancel out.

Do the origins of their coordinate systems still coincide at a time coordinate of 0 in both systems? If so, of course it is not necessary for observers at rest in these coordinate systems to be located at x=0 in each system, they can be at any position coordinate we like. But in this case I'd like a redefinition of t_a--does it refer to the time in A's frame that the photon passes x=0, or the time it passes A, or something else?

1. Are you happy with the notation regime suggested?
2. Are you happy with the concept that A and B are notionally colocated at (0,0), but they don't actually have to be colocated at that time or place?

See above, I'm not sure I understand what you're saying here.

 

[neopolitan]

I use t_a as a time interval in the A frame between an Event, and the reception of the photon coincident with that Event (or spawned by that Event).

I started writing the summary and lost it all. Very annoying.

What I mean about moving the origin of the axes is that the Event can take place whenever. But despite that, we shift the origin of the axes so that the Event is simultaneous in the A frame with (0,0).

In other words, we can work backwards. We get a photon today and discover from other reliable sources that the photon was released a distance of 10 light years away (in our frame), so we shift the origin of our t axis to back when the photon was released (in our frame) making today t = 10 years. Equally, we can be told that in three years from now, a photon will be released from the same location. We can shift the origin of our t axis forward 3 years from today, making today t = minus 3 years (knowing that the photon won't reach us until t = 10 years.

So I can shift the origin of the t-axis backwards or forwards as I like, which means I can consider any event, at any time.

If either of A and B were to not be located at the origin of their frame of reference, I would make it B.

I'm a bit perplexed by the idea that x'_a wouldn't be variable with different values of t_a.

To the same extent that x' in the equation x' = x - vt is variable with t, so to is x'_a in the equation x'_a = x_a - vt_a variable with t_a.

Also, I do believe that in the standard Lorentz Transformation x' is variable as you vary t (and indeed x).

I would agree that I would have to write x'_a(t_a) = x_a - vt_a, if I routinely saw the Lorentz Transformation written as:

$$x'(x,t)= \gamma.(x - vt)$$
$$t'(x,t)= \gamma.(t - vx/c^2)$$

But I don't.

I feel as if you are demanding more than is justified. I can do as requested if I must though.

Can you confirm that I absolutely must specify that x'_a varies as t_a varies?

cheers,

neopolitan

 

[neopolitan]

Summarising where I think we are at (including corrections in an attempt to be more rigorous).

We start with the kinematic equation for an observer A observing B who has a velocity of v towards a location which has a separation of x from A:

x' = x - vt

or

x'(t) = x - vt

which is, in words:

(separation between B and position x, in A's frame, at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

We then introduce the concept that if a photon is released from a distance of x_a away from A and it takes a period of t_a to reach A, then:

x_a = ct_a

which is, in words:

(location of the Event, in A's frame) = (speed of light)*(time interval between the Event and when a photon from the Event reaches A, in A's frame)

Using these values in the kinematic equation we have:

x'_a = x_a - vt_a

or

x'_a(t_a) = x_a - vt_a

which is, in words:

(separation between B and the location of the Event, in A's frame, when a photon from the Event reaches A, in A's frame) = (location of the Event, in A's frame) - (velocity of B in A's frame)*(time interval between the Event and when a photon from the Event reaches A, in A's frame)

Then, we want to know how things look in B's rest frame.

x'_b = ct'_b and
x_b = x'_b + vt'_b {or x_b(t'_b)}

which are, in words:

(location of Event, in B's frame) = (speed of light)*(time interval between the Event and reception of photon from the Event, in B's frame) and

(separation between B and the location of the Event, in B's frame, when a photon from the Event reaches B, in B's frame) = (location of the Event, in B's frame) + (velocity of A in B's frame)*(time interval between the Event and when a photon from the Event reaches B, in B's frame)

Since

t_a = time interval between the Event and when a photon from the Event reaches A, in A's frame

and

t'_b = time interval between the Event and when a photon from the Event reaches B, in B's frame

we have no expectation that t_a = t'_b

Happy with that?

cheers,

neopolitan

 

[JesseM]

I use t_a as a time interval in the A frame between an Event, and the reception of the photon coincident with that Event (or spawned by that Event).

Again, are you assuming A is at position x=0 in A's own rest frame? If not, when you say "reception of the photon" do you mean when the photon crosses A's worldline, or when the photon crosses the x=0 axis?

What I mean about moving the origin of the axes is that the Event can take place whenever. But despite that, we shift the origin of the axes so that the Event is simultaneous in the A frame with (0,0).

"Take place whenever" relative to what coordinate system? If you're using a coordinate system where it takes place at t=0, then it doesn't take place whenever, and if that's the starting point of your proof then everything else in the proof follows from that assumption and whatever conclusions you reach cannot simply be assumed to still hold if the Event is located somewhere else besides t=0 (if that's what you're getting at, I'm not sure). If it helps, suppose you end up proving that if in A's frame the spatial and temporal intervals between the Event at t=0 and some second event are x and t, then the spatial interval between these same pair of events in B's frame is gamma*(x - vt) and the temporal interval is gamma*(t - vx/c^2). In that case, even though your proof started from the assumption that the Event occurred at t=0 in A's frame, it would be easy to prove a lemma of the type I talked about back in post 249:

I suppose you could prove a lemma that shows that the distance and time intervals between a pair of events in a given coordinate system will be unchanged in a second coordinate system with the origin at a different location but which is at rest relative to the first (i.e. a simple coordinate transformation of the form x' = x + X₀ and t' = t + T₀ where X₀ and T₀ are constants).

So with this lemma added, you could then show that the relation between the intervals in A's frame and the intervals in B's frame will be the same even if you move the origins so that the Event is at some totally arbitrary set of coordinates. This lemma could be added to the very end of the proof. However, this will still not necessarily mean your proof is fully general; if in your proof you assume that the first Event and the second event (which together define the intervals you're dealing with in each frame) both lie along the path of a light ray, then you haven't proved that the same relation would hold for a pair of events with a timelike or spacelike separation.

In other words, we can work backwards. We get a photon today and discover from other reliable sources that the photon was released a distance of 10 light years away (in our frame), so we shift the origin of our t axis to back when the photon was released (in our frame) making today t = 10 years.

Why assume the origin was somewhere else to begin with? You don't even have to pick the placement of your axes until you've already received the photon, and at that point it's easy to position them so that the Event 10 light years away occurred at t=0, if that's all you're worried about. When dealing with SR problems you don't really have to concern yourself with these sorts of practical issues, just assume either an omniscient perspective on spacetime, or assume all coordinates are assigned indefinitely far into the future when all the events in the region of spacetime you're interested in are already known.

If either of A and B were to not be located at the origin of their frame of reference, I would make it B.

If B is not at the origin of its own frame, then does that mean B is not necessarily colocated with A at t=0 in A's frame? If it's not, then don't you have to modify the equation

I'm a bit perplexed by the idea that x'_a wouldn't be variable with different values of t_a.

t_a is a constant in any given physical scenario, is it not? It's the time coordinate of when the photon passes A, right? So if x'_a represents the distance between B and the position x_a as a function of time, this distance is varying with the time coordinate t in A's frame, not varying with t_a (unless you are using t_a to represent A's time variable as well as the specific time the photon passes A, something I requested you not do in my last post because it'd be confusing). On the other hand, if you just want to define x'_a as the distance between B and x_a at the specific time t_a when the photon passes A (or alternatively, at the specific time t'_a when the photon passes B), that's fine with me, in this case x'_a would be a constant rather than a variable. But you seemed to want x'_a to represent a distance that could vary with time rather than a distance at a specific time in post 306 when you said:

Note that in A's rest frame, the distance between the location of YDE and A does not change - therefore x_a does not change with time, but x'_a does (because x'_a is the distance between the location of YDE and B, according to A).

To the same extent that x' in the equation x' = x - vt is variable with t, so to is x'_a in the equation x'_a = x_a - vt_a variable with t_a.

Again, in any specific physical setup isn't t_a a constant? Of course you can vary the physical setup itself, but that's not what I meant when I said I thought you were making x'_a a variable--I thought that even given a particular setup (a particular choice of position x_a for the Event on the photon's worldline), x'_a represented the changing distance between B and x_a as a function of time in A's coordinate system, not the distance between B and x_a at some specific time like t_a (I based this on your comment from post 306 above).

Also, I do believe that in the standard Lorentz Transformation x' is variable as you vary t (and indeed x).

If you can vary x and t, sure, but if you pick some specific physical event then x', x, and t for that choice of event are all constants, echoing my comment about t_a and x_a being constants for a particular choice of physical setup in your scenario.

Can you confirm that I absolutely must specify that x'_a varies as t_a varies?

See above for a clarification of my meaning. If you want x'_a to be the distance between B and x_a at a specific time corresponding to some event in your setup like the photon passing A at t_a or the photon passing B at t'_a (and remember that you had actually defined x'_a in the latter way in our earlier discussions, not the former), then there's no need to call it a variable. But your comment in post 306 seemed to insist that x'_a is defined in such a way that it changes with time rather than being the distance between B and x_a at some specific time.

 

[neopolitan]

Again, are you assuming A is at position x=0 in A's own rest frame?

Yes


As for the rest, I'm a bit confused why something that seems so obvious to me is confusing for you.

I'll try again.

In A's rest frame, A is at rest.

In A's rest frame, B is not at rest.

In A's rest frame, the separation between where the Event takes, took or will take place and A is constant.

In A's rest frame, the separation between where the Event takes, took or will take place and B is not constant.

x_a is the separation between where the Event takes, took or will take place and A in A's rest frame.

x'_a is the separation between where the Event takes, took or will take place and B in A's rest frame.

Therefore, x_a is constant and x'_a is not constant.

It seems so simple to me, I can't quite grasp why it warrants such a long post about it.


For a specific time in A's frame, x'_a is defined, not varying, but not quite a constant either (because to me a constant is only a constant if you can vary something and once you pick a specific time, you don't have anything to vary in A's frame anymore, so long as you continue to talk about the same Event).

cheers,

neopolitan

 

[JesseM]

We start with the kinematic equation for an observer A observing B who has a velocity of v towards a location which has a separation of x from A:

x' = x - vt

or

x'(t) = x - vt

which is, in words:

(separation between B and position x, in A's frame, at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

We then introduce the concept that if a photon is released from a distance of xa away from A and it takes a period of ta to reach A, then:

x_a = ct_a

which is, in words:

(location of the Event, in A's frame) = (speed of light)*(time interval between the Event and when a photon from the Event reaches A, in A's frame)

Using these values in the kinematic equation we have:

x'_a = x_a - vt_a

You should also add the assumption that the Event occurs at time coordinate t=0 in A's frame, and that A is located at x=0, since otherwise this substitution wouldn't work.

(separation between B and the location of the Event, in B's frame, when a photon from the Event reaches B, in B's frame) = (location of the Event, in B's frame) + (velocity of A in B's frame)*(time interval between the Event and when a photon from the Event reaches B, in B's frame)

I assume you meant to write separation between A and the location of the Event in B's frame, right? After all, the separation between B and any given location in B's frame will be constant. Assuming that's what you meant, then it seems to me the equation would only hold if we assume that A and B are colocated at the same time as the Event occurs in B's frame. But that's obviously problematic, because we already assumed the Event was simultaneous with A and B being colocated in A's frame, and as we know they can't both be true in relativity.

 

[JesseM]

I'll try again.

In A's rest frame, A is at rest.

In A's rest frame, B is not at rest.

In A's rest frame, the separation between where the Event takes, took or will take place and A is constant.

In A's rest frame, the separation between where the Event takes, took or will take place and B is not constant.

x_a is the separation between where the Event takes, took or will take place and A in A's rest frame.

x'_a is the separation between where the Event takes, took or will take place and B in A's rest frame.

Therefore, x_a is constant and x'_a is not constant.

Yes, that's exactly what I originally thought you meant, until you made the confusing comment that x'_a varies with t_a, rather than saying it varies with t, which is something I was asking about (I know you don't like my habit of responding to your posts line-by-line, but your habit of responding to my posts in a 'gestalt' manner often means you don't answer the specific questions I ask about, and instead just repeat things I already understand without answering the questions I specifically asked for the purposes of clarifying). Again, I thought t_a was a constant (given a particular physical setup) just like x_a--t_a represents the time the photon passes A, and for a particular physical setup there's only one unique time that this happens. After all, you wrote x_a = c*t_a--if you call x_a a constant, then based on this equation you must call t_a a constant too. It's possible you are using the symbol t_a to represent both the abstract time variable in A's frame and the specific time coordinate when the photon passes A, but I already speculated in two previous posts that you might be doing this and asked you to please not use that sort of ambiguous notation if that's what's going on.

Then you also made the point that you shouldn't have to spell out that x'_a varies with time when x' is not written as x'(x,t) in the Lorentz transformation. I pointed out that given a particular choice of physical event, x and t are not variables, analogous to how given a particular choice of physical setup (distance between the Event on the path of the light ray and A at time t=0 in A's frame), x_a and t_a are not variables in your equations. Do you understand this point, and if so do you drop this particular argument for why it's unreasonable for me to ask you to write x'_a(t) in your equations?

For a specific time in A's frame, x'_a is defined, not varying

Sure, for any variable with a function of t, if you pick a specific time t it doesn't vary at that time! This is totally trivial, but it hardly proves that a quantity that varies with t is not a "variable". The point is, in a given physics problem with a well-defined physical setup, I'd call a symbol a "variable" if its value can change depending on the value of some other symbol, and a "constant" its value depends only on the setup. Is it my request that you differentiate between the two in your notation really so onerous? Just to help add some context, one of the reasons I make this request is that I anticipate that later in the proof you're probably going to want to talk about the value of x'_a(t) at a different time other than t_a, perhaps at the time t'_a in A's frame when the photon passes A; at that point it really could become genuinely confusing if you use exactly the same symbol, a problem that will be avoided if you write x'_a(t_a) for the first and x'_a(t'_a) for the second. And if I'm wrong, and your proof will never make use of x'_a at any time other than t_a, in that case making a big deal out of the fact that x'_a is a variable seems pointless, it would be much simpler just to define x'_a as the distance between B and the position of the event at the specific time t_a when the photon passes A.

 

[neopolitan]

Fixing (corrections and clarifications are highlighted - I accept that wherever I need to make a clarification this is as bad as being wrong, I don't intend to defend being wrong - or being so unclear as to necessitate a clarification);

We start with the kinematic equation for an observer A observing B who has a velocity of v towards a location which has a separation of x from A:

x' = x - vt

or

x'(t) = x - vt

which is, in words:

(separation between B and position x, in A's frame, at time t in A's frame) = (position x in A's frame) - (velocity of B in A's frame)*(time t in A's frame)

We then introduce the concept that if at t=0 a photon is released from a distance of x_a away from A and it takes a period of t_a to reach A and A is located at x=0, then:

x_a = ct_a

which is, in words:

(location of the Event, in A's frame) = (speed of light)*(time interval between colocation of A and B and when a photon from the Event reaches A, in A's frame)

Using these values in the kinematic equation we have:

x'_a = x_a - vt_a

or

x'_a(t_a) = x_a - vt_a

which is, in words:

(separation between B and the location of the Event, in A's frame, when a photon from the Event reaches A, in A's frame) = (location of the Event, in A's frame) - (velocity of B in A's frame)*(time interval between colocation of A and B and when a photon from the Event reaches A, in A's frame)

Then, we want to know how things look in B's rest frame. If at t'=0 the photon released as described before is at a distance of x'_b away from B and it takes a period of t'_b to reach B and B is located at x'=0, then:

x'_b = ct'_b and
x_b = x'_b + vt'_b {or x_b(t'_b)}

which are, in words:

(location of Event, in B's frame) = (speed of light)*(time interval between colocation of A and B and reception of photon from the Event, in B's frame) and

(separation between A and the location of the Event, in B's frame, when a photon from the Event reaches B, in B's frame) = (location of the Event, in B's frame) + (velocity of A in B's frame)*(time interval between colocation of A and B and when a photon from the Event reaches B, in B's frame)

Since

t_a = time interval between colocation of A and B and when a photon from the Event reaches A, in A's frame

and

t'_b = time interval between colocation of A and B and when a photon from the Event reaches B, in B's frame

we have no expectation that t_a = t'_b

I'm aware that the event simultaneous with t=0 and the event simultaneous with t'=0 are not simultaneous with each other. However, each event used is colocated with the relevant observer (notionally, if A and B are timing events, the only events they can give accurate time values to are "colocation of self with other observer" and "colocation of self with photon").

The point I have to make clear again is that we only know what happened at an event once information (or photon from the event) reach us. Then we work backwards.

If A receives a photon at t_a from an event at t=0, then when did that same photon pass B? What is t'_b in terms of t_a and x_a?

What is x'_b in terms of t_a and x_a?

Can we work it out?

I think we can.

 

[neopolitan]

Yes, that's exactly what I originally thought you meant, until you made the confusing comment that x'_a varies with t_a, rather than saying it varies with t, which is something I was asking about (I know you don't like my habit of responding to your posts line-by-line, but your habit of responding to my posts in a 'gestalt' manner often means you don't answer the specific questions I ask about, and instead just repeat things I already understand without answering the questions I specifically asked for the purposes of clarifying). Again, I thought t_a was a constant (given a particular physical setup) just like x_a--t_a represents the time the photon passes A, and for a particular physical setup there's only one unique time that this happens. After all, you wrote x_a = c*t_a--if you call x_a a constant, then based on this equation you must call t_a a constant too. It's possible you are using the symbol t_a to represent both the abstract time variable in A's frame and the specific time coordinate when the photon passes A, but I already speculated in two previous posts that you might be doing this and asked you to please not use that sort of ambiguous notation if that's what's going on.

Then you also made the point that you shouldn't have to spell out that x'_a varies with time when x' is not written as x'(x,t) in the Lorentz transformation. I pointed out that given a particular choice of physical event, x and t are not variables, analogous to how given a particular choice of physical setup (distance between the Event on the path of the light ray and A at time t=0 in A's frame), x_a and t_a are not variables in your equations. Do you understand this point, and if so do you drop this particular argument for why it's unreasonable for me to ask you to write x'_a(t) in your equations?

Sure, for any variable with a function of t, if you pick a specific time t it doesn't vary at that time! This is totally trivial, but it hardly proves that a quantity that varies with t is not a "variable". The point is, in a given physics problem with a well-defined physical setup, I'd call a symbol a "variable" if its value can change depending on the value of some other symbol, and a "constant" its value depends only on the setup. Is it my request that you differentiate between the two in your notation really so onerous? Just to help add some context, one of the reasons I make this request is that I anticipate that later in the proof you're probably going to want to talk about the value of x'_a(t) at a different time other than t_a, perhaps at the time t'_a in A's frame when the photon passes A; at that point it really could become genuinely confusing if you use exactly the same symbol, a problem that will be avoided if you write x'_a(t_a) for the first and x'_a(t'_a) for the second. And if I'm wrong, and your proof will never make use of x'_a at any time other than t_a, in that case making a big deal out of the fact that x'_a is a variable seems pointless, it would be much simpler just to define x'_a as the distance between B and the position of the event at the specific time t_a when the photon passes A.

I don't intend to use a value of x'_a that is different from its value at t_a.

I don't intend to use a value of x_b that is different from its value at t'_b.

I don't intend use a value of x_a other than such that x_a = c.t_a

I don't intend use a value of x'_b other than such that x'_b = c.t'_b.

Does that make things easier?

If I do find myself using anything other than these, I will try to mark them accordingly (but I really don't think that I will).

cheers,

neopolitan

 

[sylas]

I don't intend to use a value of x'_a that is different from its value at t_a.

What does this even mean?

Is x'_a a constant, or a variable? If you mean a constant, why the heck are you speaking of its value at certain time? If you mean a variable, why the heck would you only use a single value?

Isn't (x'_a, t'_a) just the co-ordinates of the event "photon passes A" in the frame of reference of B?

 

[neopolitan]

Isn't (x'_a, t'_a) just the co-ordinates of the event "photon passes A" in the frame of reference of B?

The post you quoted was in response to a specific concern from JesseM that I would go changing the meaning of x'_a. I don't intend to.

He got to that because I noted at one point that (in general) while in the A frame x_a does not change, x'_a does. But my (specific scenario driven) derivation centres around events which lock in values of x_a, t_a and hence x'_a. So in the scenario I describe, x_a, t_a and x'_a all have one value. So fixed are they that in earlier posts we assigned them numbers.

In answer to the question you posed here, no.

x'_a is the separation between B and where the photon was at t = 0 in the A frame (x = separation, ' = between B and the Event, _a = in the A frame or according to A).

cheers,

neopolitan

It may be worth mentioning that I am keeping the prime from the kinematic equation x' = x - vt

While I understand that this may cause concern because while I focus on observer A, and that that would make a few people consider that primes refer to B's rest frame, those people might be happier to know that the equations I end up with are:

x'_b = gamma.(x_a - vt_a)
t'_b = gamma.(t_a - vx_a/c²)

which is a confluence of the primed is the B frame, unprimed is the A frame and _b is the B frame, _a is the A frame.

 

[sylas]

The post you quoted was in response to a specific concern from JesseM that I would go changing the meaning of x'_a. I don't intend to.

He got to that because I noted at one point that (in general) while in the A frame x_a does not change, x'_a does. But my (specific scenario driven) derivation centres around events which lock in values of x_a, t_a and hence x'_a. So in the scenario I describe, x_a, t_a and x'_a all have one value. So fixed are they that in earlier posts we assigned them numbers.

In answer to the question you posed here, no.

x'_a is the separation between B and where the photon was at t = 0 in the A frame (x = separation, ' = between B and the Event, _a = in the A frame or according to A).

cheers,

neopolitan

Thanks... but I am still finding this incredibly hard to follow.

You've said "x'_a is the separation between B and where the photon was at t = 0 in the A frame". Distance WHEN? At t=0 also? t according to whom? You say it has one value. But then you've also said that x'_a can "change" in the A frame? How can that possibly be?

I have trouble following along when you speak of a "location". What is a fixed location in one frame is not a fixed location in another. I think it would be clearer if you stick to "events", so that you can sensibly speak of one event in several different frames.

You scenario is this, isn't it? It involves three particles: A, B and photon. A and B are moving at constant velocity v relative to each other. The events of interest occur in this order.

• A passes by B (co-located).
• Photon passes by B.
• Photon passes by A.

Is that right? You've also added another event of photon being "emitted".

The distance between events A and B (photon passing by A and photon passing by B) as observed by the particles A and B are related by the Doppler shift factor, are they not? Multiply, or divide the distance by
$$\sqrt{\frac{c-v}{c+v}}$$
to get the distance for the other observer. The distance is greater for the particle that the photon passes by first.

Cheers -- sylas

 

[neopolitan]

sylas,

I do appreciate your interest, but you might notice that a lot has come before this. If I reply to you, Jesse will reply to my replies to you (it's happened before) and we will end up going over old ground again which is something I am trying to avoid.

In general, x'_a(t) is variable with t. Specifically, x'_a(t) is fixed with a fixed value of t=t_a.

The scenario is framed such that x_a(0) = c.t_a, in other words a time interval of t_a after t=0 (in the A frame), a photon passes A since it was initially the right distance away to cover that distance in that time.

At the time at which the photon passes A, B has traveled a distance towards where the event took place and in A's frame that is:

x'_a(t_a) = x_a - v.t_a

(the separation between B and where the event took place at the time at which the photon from the event passes A, in the A frame) = (the separation between A and where the event took place) - (the distance that B has moved towards where the event took place in the time it took for a photon to travel from the event to A)

Note, I am not specifically writing this to explain to you, I am writing it in a format that JesseM has said is necessary for it to be explained.

Now, I suspect that the method for explaining to JesseM just possibly won't be as suitable for explaining to you. If that is the case, can I suggest that you go back into the earlier posts, find an explanation which seems to suit you more, and I can try to address your questions in a separate thread?

cheers,

neopolitan

 

[JesseM]

I don't intend to use a value of x'_a that is different from its value at t_a.

I don't intend to use a value of x_b that is different from its value at t'_b.

I don't intend use a value of x_a other than such that x_a = c.t_a

I don't intend use a value of x'_b other than such that x'_b = c.t'_b.

Does that make things easier?

In that case, why introduce the complication of saying x'_a is a variable but x_a is a constant? You could easily make x'_a a constant just by specifically defining it as the separation at time t_a when the photon passes A, not the separation at an arbitrary time t in A's frame.

Just as a reminder though, back when we were going through the numerical example where you put numbers to these values, you did define the symbol x'_a in terms of t'_a, the time the photon passed B (both x'_a and t'_a had the value 5).

 

[sylas]

Now, I suspect that the method for explaining to JesseM just possibly won't be as suitable for explaining to you. If that is the case, can I suggest that you go back into the earlier posts, find an explanation which seems to suit you more, and I can try to address your questions in a separate thread?

S'okay. I am perfectly comfortable with relativity and don't need it explained to me. I can see I am not helping here, and withdraw. Sorry for the distraction!

My main aim was to suggest, gently, that you are not doing a very good job of giving clear and unambiguous definitions of what you mean. I'm glad you didn't take offense at that; I wanted to say it without coming across as being too negative. But I still find it really hard to follow what you mean with notation or use of language, and I don't think this is just me, or because it is non-standard. The problem is that it is almost always ambiguous. You evidently have a clear idea what you mean. I don't.

It should be possible to express whatever it is you mean with less words and repetition. All you need is to avoid any potential ambiguity for what notation refers to; and then pretty much any of the regulars who have struggled to follow these threads will get it, IMO. It's not a problem of finding the "right" explanation for different people.

When explanations refer to the distance to a "location", rather than an event, there's a potential ambiguity as to what the location means in different frames and times. A "location" without an associated particle usually means a fixed distance co-ordinate, or worldline with zero velocity; but that depends on the observer and I often don't know what observer is intended. Referring to a specific event, however, is nearly always crystal clear.

The main answer here is that observers A and B measure different distances from the event "photon passes B" to the event "photon passes A". If the photon passes by B and then A, and if v is their relative velocity (+ve for moving apart), then the distance between these two events d_A for observer A is related to distance d_B for observer B by

$$d_A = d_B \sqrt{\frac{c-v}{c+v}}$$​

You can show this with the Lorentz transformations; and there may be other ways to get the right answer.

 

[JesseM]

Fixing (corrections and clarifications are highlighted - I accept that wherever I need to make a clarification this is as bad as being wrong, I don't intend to defend being wrong - or being so unclear as to necessitate a clarification);

OK, the clarified version looks clear to me.

I'm aware that the event simultaneous with t=0 and the event simultaneous with t'=0 are not simultaneous with each other. However, each event used is colocated with the relevant observer

Each event you use to define the time intervals, yes. The "Event(s)" on the photon's worldline used to define x_a and x'_b aren't colocated with the observers, of course.

If A receives a photon at t_a from an event at t=0, then when did that same photon pass B?

You mean, what time in A's frame did the photon pass B? This is a time you haven't defined a symbol for yet, although in the earlier discussion you defined this as t'_a.

What is t'_b in terms of t_a and x_a?

Note that t'_b and t_a/x_a don't refer to intervals between the same pair of events, so if you show a certain relation between these values it won't necessarily prove anything about the intervals in different frames between a single pair of events as in the the Lorentz transformation. Also note that in the Lorentz transformation equation it's not only assumed you're talking about intervals between a single pair of events, but it's also assumed that when calculating the intervals you're being consistent about the order in which you're taking the events. For example, x_a and t_a could both be understood as space and time intervals between the same pair of events (photon passing A) and (Event on photon's worldline that's simultaneous with A&B being colocated) even if you didn't choose to define them in terms of this pair, so if t_a was to be defined as (time coordinate of photon passing A) - (time coordinate of Event on photon's worldline that's simultaneous with A&B being colocated) in order to make it a positive number, then that means in order to be consistent we would have to define x_a as (position coordinate of photon passing A) - (position coordinate of Event on photon's worldline that's simultaneous with A&B being colocated), so if you assume this Event has a positive position position coordinate that would make the interval x_a negative according to the above definition. I think that in your notation you are just defining x_a as the absolute value of the distance between A and the Event, so it would be positive rather than negative; in this case the physical meaning of the equation you derive relating these quantities will be quite different from the physical meaning of the Lorentz transformation relating intervals between a single pair of events calculated using a consistent order for the events.

Just to check where you're going with this, do you intend to derive an equation that has the same physical meaning as the Lorentz transformation, or do you just intend to derive an equation which looks superficially similar but whose physical meaning is different?