- #1
nish95
- 12
- 0
Hi everyone,
I was looking to develop my physical insight when I encountered this book by Lewis Caroll Epstein. For the crosswind problem, I couldn't understand the author's explanation; in particular, his concept of "artificial wind," and the force being larger in this case than the previous one. I understand that the sail will sag when the speed of the boat in the direction of normal to the sail is equal to that of wind in the same direction. I have attached the relevant pages of the book below.
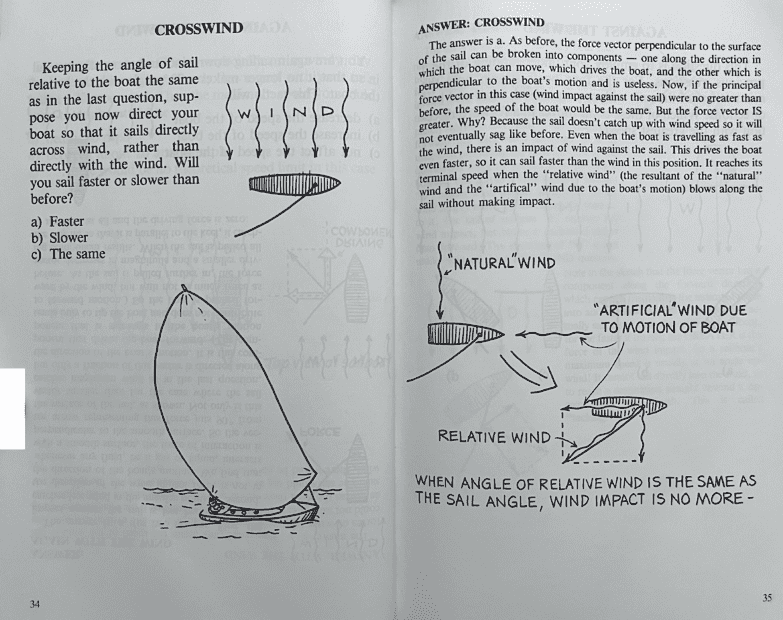
I was looking to develop my physical insight when I encountered this book by Lewis Caroll Epstein. For the crosswind problem, I couldn't understand the author's explanation; in particular, his concept of "artificial wind," and the force being larger in this case than the previous one. I understand that the sail will sag when the speed of the boat in the direction of normal to the sail is equal to that of wind in the same direction. I have attached the relevant pages of the book below.