casualguitar
- 503
- 26
- TL;DR Summary
- How can the conservation/Navier Stokes equations (mass, momentum,energy) be modified to model two phase flow in a porous media?
Previously, I have seen the derivation of the energy conservation equations for simulation of single phase flow in a porous media (a packed bed). These are the energy equations for the solid and fluid respectively:
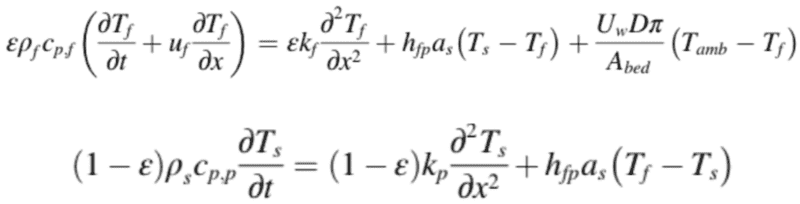
I understand the derivation, however, these equations will only work when the fluid flow is single phase. I would like to derive this equation (and likely the mass/momentum equations if necessary), for two phase fluid flow i.e. with a phase change
The mass, momentum, and energy conservation equations:
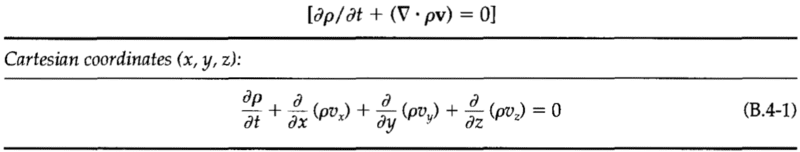
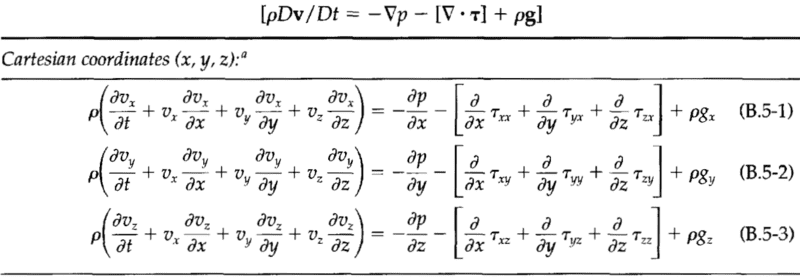
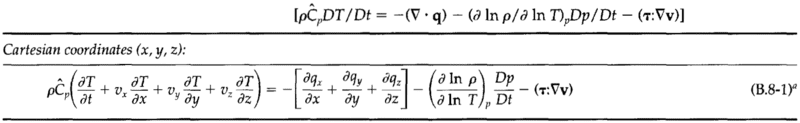
The goal here is to model the phase change of the fluid as it flows through the porous bed.
Requirements here are to model the temperature of the solid and fluid over time, and to track the phase fronts over time. Inside the phase change segment of the bed I would like to track the quality. I believe the solid energy conservation equation is not affected by the phase change, and we do not need mass/momentum conservation for the solid as it is static.
So this leaves a mass,momentum, and energy balance for the two phase fluid
I have set up a code base that allows calculation of almost any property for a pure fluid or mixture that would be required for this model. So essentially the derivation of the conservation equations are all that are remaining to model this system.
So to the question - how can I get started with deriving mass/momentum/energy (MME) equations that track the goal parameters? Is this a trivial change to the equations above?
Side note - I am also including this energy conservation equation that was previously flagged as being useful in solving this problem:
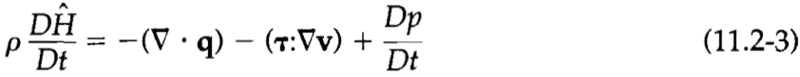
I understand the derivation, however, these equations will only work when the fluid flow is single phase. I would like to derive this equation (and likely the mass/momentum equations if necessary), for two phase fluid flow i.e. with a phase change
The mass, momentum, and energy conservation equations:
The goal here is to model the phase change of the fluid as it flows through the porous bed.
Requirements here are to model the temperature of the solid and fluid over time, and to track the phase fronts over time. Inside the phase change segment of the bed I would like to track the quality. I believe the solid energy conservation equation is not affected by the phase change, and we do not need mass/momentum conservation for the solid as it is static.
So this leaves a mass,momentum, and energy balance for the two phase fluid
I have set up a code base that allows calculation of almost any property for a pure fluid or mixture that would be required for this model. So essentially the derivation of the conservation equations are all that are remaining to model this system.
So to the question - how can I get started with deriving mass/momentum/energy (MME) equations that track the goal parameters? Is this a trivial change to the equations above?
Side note - I am also including this energy conservation equation that was previously flagged as being useful in solving this problem:

