- #1,016
zoki85
- 1,198
- 230
Dunno, maybe they had 69 barrels and 22 barrels respectively before paying duty?
No, this isn't it. The number of barrels given is exactly what they arrived at the gates of Paris with.zoki85 said:Dunno, maybe they had 69 barrels and 22 barrels respectively before paying duty?
So, looking at this new way, what is the value of each barrel of wine, and what is the duty payable on it?zoki85 said:Ok, my last try on it. If the barrels they are paying with are considered money and not goods, they are actually paying duty for 59 barrels and 18 barrels respectively. So the equations would be:
59x=5y+40
18x=2y-40
?
That doesn't interest me anymore now if you confirm this way that was the catch;)zoobyshoe said:So, looking at this new way, what is the value of each barrel of wine, and what is the duty payable on it?
There never was a catch. There is an ambiguity. You could assume, as you did, that they were required to pay customs duty on the whole amount they originally wanted to take into Paris, (even though they wouldn't actually be taking that amount in because they were using part of it to pay the duty) or, you could assume they would only be required to pay duty on the amount they actually ended up taking in, 59 and 18 barrels, respectively.zoki85 said:That doesn't interest me anymore now if you confirm this way that was the catch;)
Correct! And nice graphic work!zoki85 said: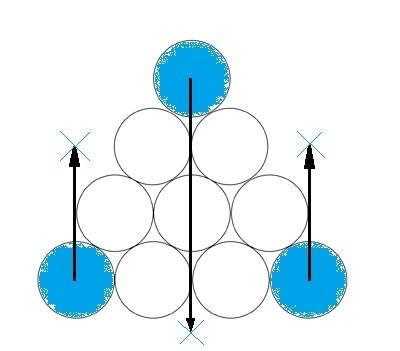
Yes.Enigman said:5.5, 6.5, 7, 4.5, 3.5
Thanks. I'll have to study that a while to see if I can make sense out of it.Enigman said:I did it using Matrix method of solving equations.
http://www.mathsisfun.com/algebra/systems-linear-equations-matrices.html
zoki85 said:Cute little puzzle for people who like chess.
White has just made the last move and the game ended in a draw (stalemate-see diagram). Determine that move.
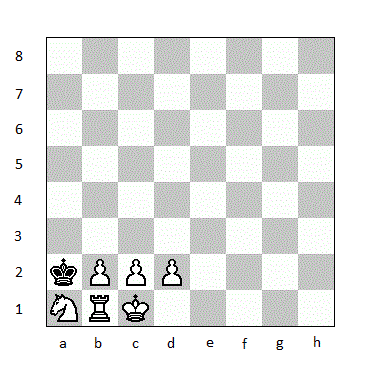
This puzzle was beyond me, and I'm amazed mfb and collinsmark were able to figure out the last move involved taking a specific piece which is no longer even on the board. Are they PSYCHIC?zoki85 said:That's right, king takes knight on C1 :)
zoobyshoe said:This puzzle was beyond me, and I'm amazed mfb and collinsmark were able to figure out the last move involved taking a specific piece which is no longer even on the board. Are they PSYCHIC?
Haha, doing a little of retrograde analysis certainly helps more heredrizzle said:They must be.oo)
I'm confused. Does the image depict the situation just after white made the move it regretted, or does it depict the situation before white made the move it regretted?zoki85 said:White just played a move (diagram), but instantly noticed that wasn't the best move.
With allowance of Black, White takes back the move, and then executes a new move giving a checkmate with it.
Can you reconstruct the moves?
Correct:)consciousness said:Nice one
White took on black's bishop on e8 with his pawn promoting to a knight. Best was pawn to f8 knight promotion resulting in mate.
[\spoiler]
zoki85 said:White just played a move (diagram), but instantly noticed that wasn't the best move.
zoobyshoe said:I'm confused. Does the image depict the situation just after white made the move it regretted, or does it depict the situation before white made the move it regretted?