You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Field Definition and 1000 Threads
-
L
I Proving Antisymmetry of Electromagnetic Field Tensor with 4-Force
I've already made a post about this topic here, but I realized that I didn't understand the explanation on that post. in Chapter 7 of Rindler's book on relativity, in section about electromagnetic field tensor, he states that _and introducing a factor 1/c for later convenience, we can ‘guess’... -

I How to prove that some fields are different aspects of one general field?
Hi! I know some theorists believe all quantum fields and gravitational field are different aspects of one universal field. What does that formally (e.g. mathematically) mean "to be different aspects of" and how can one prove, let's say, fields A and B are different aspects of C? By the way, I... -

Continuity equation of the electric field
According to the continuity equation of the electric field (i.e., ▽·Ε = 0) a decrease in cross-section area will increase the electric field strength, Why is that?- speaknow
- Thread
- Replies: 4
- Forum: Electromagnetism
-
S
B Defining the derivative of a vector field component
I'm reading 'Core Principles of Special and General Relativity' by Luscombe, specifically the introductory section on problems with defining usual notion of differentiation for tensor fields. I'll quote the relevant part: Since the equation above is a notational mess, here's my attempt to...- Shirish
- Thread
- Replies: 7
- Forum: Differential Geometry
-

Gadget: Levitating Earth (magnetic field)
I bought a fun gadget from China. It's a model of Earth levitating in a magnetic field. I filmed it in operation to share with my friends, but I thought I would share it on PF too :smile:. I bought it online here. Film clip: I speak Swedish in the clip, and what I'm saying is this: "...- DennisN
- Thread
- Replies: 2
- Forum: Earth Sciences
-
N
A General Covariance in Quantum Field Theory
All physical laws have to be Lorentz invariant according to a lecture I just watched. Why is general covariance (which is more general than Lorentz invariance) not a requirement for all laws of physics? Are there any quantum gravity theories that take the approach of adding general covariance to...- Newton-reborn
- Thread
- Replies: 11
- Forum: Quantum Physics
-
H
B Alpha particle in a force field depiction
Hello, I was glazing through what I would consider an advanced physics textbook and I saw this image. It is a schematic picture of an alpha-particle in a field of an atom. Now, can someone get me started on what (and why and how) is going on in it? Especially with the fraction with pi.- hawkslime
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-

Calculating the magnetic field in this seemingly simple case?
A classic example in textbooks is calculating the magnetic field inside a solenoid of length ##l## with ##N## turns and making the assumption that the magnetic field inside the solenoid is pretty uniform and outside it is 0. Using Ampere's law ## \oint_C \vec B \cdot d \vec l = \mu_0 I_{through}...- Abdullah Almosalami
- Thread
-
- Tags
- Field Magnetic Magnetic field
- Replies: 3
- Forum: Electromagnetism
-

Angle of deviation from a magnetic field
The beam of protons are directed towards the axis of the cylinder, perpendicular to the direction of the field. While traveling through the cross-section of the cylinder, the proton beam experiences a magnetic force, which tends to move the beam in a circular orbit of the radius given by: r =...- tanaygupta2000
- Thread
- Replies: 5
- Forum: Introductory Physics Homework Help
-

Electric field in a spherical shell
So for the Gaussian theorem we know that $$ \frac{Q}{e} = \vec E \cdot \vec S $$ Q's value is known so we don't need to express it as $$Q=(4/3)\pi*(R_2 ^3-R_1 ^3)*d$$ where d is the density of the charge in the volume. I've expressed the surface $$S=4\pi*x^2$$ where x is the distance of a point...- curiosissimo
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-
M
Electric Field of Point Charge at y=r and an Infinitely Long Cylinder
Let point charge q be at y=r. Let there be an infinite conducting plane along the x-axis and z-axis that is neutrally charged. In this case, the method of mirror charges can be used. The plane is replaced by a point charge -q at y=-r. The electric field for y > 0 is the same in both cases...- MrBlank
- Thread
- Replies: 9
- Forum: Electromagnetism
-

Is it possible to measure the general amount of electromagnetic field
We relating to an electromagnetic radiation as waves. and in waves there is maximum point and minimum point but when there is permanent electromagnetic level there is no disorder or weave . so is it possible to measure it in blank space relative to other places- danielhaish
- Thread
- Replies: 11
- Forum: Electromagnetism
-

Quantum Is Zuber's Quantum Field Theory textbook any good?
Hi, I have been studying Quantum Field Theory this semester! It seems that Shwartz and Peskin are the most popular choices when it comes to studying QFT. But apparently my professor have another "old" preference. He strongly suggested that we learn QFT from Zuber's book. I have looked at the...- Phylosopher
- Thread
- Replies: 2
- Forum: Science and Math Textbooks
-
E
Ball rolling in a magnetic field
I first found the Lorentz force on the ball as a whole$$\vec{F}_m = \iiint_V \rho(\omega \times \vec{r} + \vec{V})\times \vec{B} dV = \rho \vec{\omega} \times \left( \iint_V \vec{r} dV \right) \times \vec{B} + \rho \iiint_V \vec{V} \times \vec{B} dV = Q\vec{V} \times \vec{B}$$due to the...- etotheipi
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Resultant field at the center of two semicircular current arcs
So the magnetic field induced at the center of a current-carrying loop is given by: B = μ0 i /2r where r is the radius of the loop In the case of a semi-circular loop, this becomes B = μ0 i /4r In the question, i = 2A, r1 = 1m and r2 = 2m So, field induced at the center of first semicircular...- tanaygupta2000
- Thread
- Replies: 8
- Forum: Introductory Physics Homework Help
-
D
Alternator Field Winding Question
I have an older 12 volt battery-charging 1979 Sencenbaugh wind generator that I am testing. It has an 3 phase alternator with a field winding that must be excited, as opposed to the newer "permanent magnet" alternators. The manual says that 60 watts maximum should go to the field winding...- doubledipsoon
- Thread
-
- Tags
- Alternator Field Winding
- Replies: 3
- Forum: Electrical Engineering
-
R
B Gravitational Field Representation: Why 1-Plane?
How did you find PF?: Surfing web Can someone advise on this? In most diagrams showing how mass effects the gravitation field (earth for instance), bending fabric of space, it is demonstrated on one plane. Why is it shown this way and is there any other way of illustrating this?- roachth1
- Thread
- Replies: 19
- Forum: Special and General Relativity
-
S
B Understanding how coordinates change under the flow of a vector field
[Ref. 'Core Concepts in Special and General Relativity' by Luscombe] Let ##M,M'## be manifolds and ##\psi:M\to M'## a diffeomorphism. Even if ##\psi## weren't a diffeomorphism, and instead just a smooth map, the coordinates of the pushback of ##\mathbf{t}\in T_p(M)##, would be related to the...- Shirish
- Thread
- Replies: 1
- Forum: Special and General Relativity
-
L
Magnetic field of a rotating disk with a non-uniform volume charge
-------------------------------------------------------------------------------------------------------------------------------------------------- This was a problem introduced during my classical electrodynamics course. I am not 100% sure, but I think I've solved up to problems (a) and (b) as...- Light bulB 6626
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
F
Why does an alpha particle curve less in a magnetic field than a beta?
Suppose you are analyzing this image. The question to answer is: Explain why the alpha particle's path has a larger radius than either of the beta particle paths. Justify your answer using either momentum or charge-to-mass ratio. When you are answering this, suppose you know that , in...- flintstones
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-

Cylindrical Halbach array with a vertical magnetic field?
Similar to what is shown here, except the south side would be the weak side of the array. A link to purchase one of these or at least the magnetic field arrangement would be very helpful. Thanks in advance.- rayjbryant
- Thread
- Replies: 18
- Forum: Electromagnetism
-

Vector potential ##\vec A## in terms of magnetic field ##\vec B##
My solution is making an analogy of the ##\text{Relevant equations}## as shown above, starting from the equation ##\vec \omega = \frac{1}{2} \vec \nabla \times \vec v##. We have ##\vec B = \vec \nabla \times \vec A = \frac{1}{2} \vec \nabla \times 2\vec A \Rightarrow 2\vec A = \vec B \times...- brotherbobby
- Thread
- Replies: 26
- Forum: Advanced Physics Homework Help
-

Deflection of magnetic dipoles by a magnetic field
I'm reading about the Stern–Gerlach experiment and the only part that confuses me is how a magnetic field would deflect particles with magnetic dipoles instead of just rotating them. In this case the magnetic field is non-uniform, but it still seems intuitively strange to me since magnetic...- snoopies622
- Thread
- Replies: 2
- Forum: Electromagnetism
-
M
Weird condition describing symmetry transformation
I'm a bit confused about the condition given in the description of the symmetry transformation of the filed. Usually, given any symmetry transformation ##x^\mu \mapsto \bar{x}^\mu##, we require $$\bar\phi (\bar x) = \phi(x),$$ i.e. we want the transformed field at the transformed coordinates to...- Markus Kahn
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
S
A Converting between field operators and harmonic oscillators
Suppose we have a Hamiltonian containing a term of the form where ∂=d/dr and A(r) is a real function. I would like to study this with harmonic oscillator ladder operators. The naïve approach is to use where I have set ħ=1 so that This term is Hermitian because r and p both are.*...- SupernerdSven
- Thread
- Replies: 2
- Forum: Quantum Physics
-
H
Deflection of a Magnet in an Inhomogenous Magnetic Field
Say I've got a magnet flying through empty space in a homogenous magnetic field. The magnet precesses and flies in a straight path. Now make that magnetic field inhomogenous. The magnet precesses and flies in a curved path. What I can't figure out is why the path is curved. It is because...- Hornbein
- Thread
- Replies: 5
- Forum: Electromagnetism
-
I Understanding the wrong way to quantize the Dirac Field | Part 1
I've been studying Tong's beautiful chapter (pages 106-109; See also Peskin and Schroeder pages 52-58), together with his great lectures at Perimeter Institute, on how to quantize the following Dirac Lagrangian in the wrong way $$\mathscr{L}=\bar{\psi}(x)(i\not{\!\partial}-m)\psi(x) \tag{5.1}$$...- JD_PM
- Thread
-
- Tags
- Dirac Dirac field Field
- Replies: 4
- Forum: Quantum Physics
-
S
Force acting on a current carrying conductor within a magnetic field
I am new to this forum, and this is my first post. Please bear with me if my query has any inaccuracies. In the attached figure, a coil is wrapped around the central arm of a flat H-shaped thin metallic plate (such as iron). DC current flows through the coil and magnetizes the arm. At the...- sss
- Thread
- Replies: 2
- Forum: Electromagnetism
-
P
B Derivative of a constant scalar field at a point
Wikipedia defines the derivative of a scalar field, at a point, as the cotangent vector of the field at that point. In particular; The gradient is closely related to the derivative, but it is not itself a derivative: the value of the gradient at a point is a tangent vector – a vector at each...- Phinrich
- Thread
- Replies: 2
- Forum: Differential Geometry
-

Does moving an insulating cylinder produce a magnetic field?
Suppose that we have an insulating cylinder with ##\rho_q##. If i move the cylinder towards ##+\hat{n}##, will it produce a magnetic field? My assumption is that since we have an insulator, then the electrons are bound and there cannot be a current, thus a magnetic field is not produced. Also...- lelouch_v1
- Thread
- Replies: 5
- Forum: Electromagnetism
-

Increasing electric potential and electric field
Hello everybody! I want to check out if I've solved correctly: ##\Delta{V}=-E\Delta{x}## ##\dfrac{\Delta{V}}{\Delta{x}}=-E## ##\dfrac{15\;V}{10^{-2}\;m}=-E## ##1,5\times{10^3}\;N/C=-E## ##\vec{E}## direction it's oriented into the XY plane Thanks!- mcastillo356
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-

A Gravitational Energy: Field x Moment
Hello! I was wondering if it is possible to express the gravitational energy as a product of the gravitational field by a moment, as we do with the magnetic and electric energy? Would this require the existence of bodies with negative mass? How could we relate this to the existence or total...- jaumzaum
- Thread
- Replies: 4
- Forum: Special and General Relativity
-
M
What are the prerequisites to study quantum field theory?
Summary:: What are the prerequisites to study quantum field theory? What are the prerequisites to study quantum field theory?- MOKHTAR
- Thread
- Replies: 3
- Forum: STEM Academic Advising
-

What does a magnetic field feel like?
https://blog.nationalgeographic.org/2014/01/03/dogs-sense-Earth's-magnetic-field/"...the first study showing a mammal not only being able to sense it, but also to exhibit a specific behavior in response to natural magnetic field variations. " In my view, dogs are nearer human consciousness than...- DaveC426913
- Thread
-
- Tags
- Field Magnetic Magnetic field
- Replies: 3
- Forum: Biology and Medical
-
J
Electric field produced by a uniform charge density on a wall
I couldn't solve the question. Can you help me?- Jamesdn
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-

Does a Capacitor Have a Magnetic Field?
.- Fabio97
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-

Properties of symmetric magnetic field around ##Z## axis (cylinder)
I am trying to understand but without a succes why symmetric magnetic field around ##Z## axis make that ##\hat \phi## magnetic field is zero I can't understand why it physically happens and also how can I derive it mathematically? What does the word symmetric means when talking about magnetic...- sagigever
- Thread
- Replies: 4
- Forum: Electromagnetism
-
E
Electric field within a battery
I've been reading through this paper to try and get a better understanding of how batteries work. The analysis there is fine (they consider a voltaic cell to charge a capacitor in order to derive ##\Delta V=\varepsilon##, and go via an energy route), but it doesn't really touch upon the fields...- etotheipi
- Thread
- Replies: 51
- Forum: Electromagnetism
-
R
Electric field at (0,0) for this charged square conductor
Can we assume that square charge resembles a sphere shell, and think like electric field at sphere shell's center is 0.- requied
- Thread
- Replies: 8
- Forum: Introductory Physics Homework Help
-
R
Possible to network in one's field while learning new science?
Or at least honing ones scientific skill/knowledge? How would one go about this? NOTE: I am talking about a non-pandemic or otherwise non-emergency condition.- random_soldier
- Thread
- Replies: 5
- Forum: General Discussion
-
R
Force field suitable for studying silica crystal
I need some advice and help please -Is There a two body force field suitable to study silica crystal or alpha quartz crystal? it's okay to gives Approximate results. - Is the BKS force field suitable for silica crystal? - If there are other simple terms of force field for studying the silica...- reguieg yssaad
- Thread
- Replies: 2
- Forum: Materials and Chemical Engineering
-
F
Non-circular motion of a particle in a perpendicular constant magnetic field
There's a constant magnetic field B. If a particle is acted on by a force qv*B (* cross) only, and the initial velocity v0 is normal to B, is the motion certainly a circular one (for any m, q, v0)? mv''=qv*B If one solves this equation (vector), it doesn't seem obvious.- feynman1
- Thread
- Replies: 5
- Forum: Electromagnetism
-

Magnetic field in a rotating uniformly-charged infinite cylinder
I am sure I need to use Amper's law to do that. if I use the equation I mentioned above it easy to calculate the right side of the equation but I have problem how to calculate the path integral. I know from right hand rule that the magnetic field will point at $$Z$$ and the current is in...- sagigever
- Thread
- Replies: 36
- Forum: Introductory Physics Homework Help
-

I Parallel transport vs Lie dragging along a Killing vector field
Hi, I would like to ask for a clarification about the difference between parallel transport vs Lie dragging in the following scenario. Take a vector field ##V## defined on spacetime manifold and a curve ##C## on it. The manifold is endowed with the metric connection (I'm aware of it does exist...- cianfa72
- Thread
- Replies: 20
- Forum: Special and General Relativity
-
K
I Quantum Field Operators for Bosons
Consider the field creation operator ψ†(x) = ∫d3p ap†exp(-ip.x) My understanding is that this operator does not add particles from a particular momentum state. Rather it coherently (in-phase) adds a particle created from |0> expanded as a superposition of momentum eigenstates states...- knowwhatyoudontknow
- Thread
- Replies: 4
- Forum: Quantum Physics
-

Force & energy in cutting and stretching magnetic field lines?
I have an ordinary switchable magnet for holding tools to a lathe. It's like a magnetic force gearbox, but I can't quite understand the force multiplication. When placed on a steel surface the switch force is approximately ~5N on both finger and thumb at 1.5cm radius acting over a 3cm arc...- Luke2642
- Thread
- Replies: 3
- Forum: Electromagnetism
-
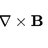
Magnetic field (correction term)
Ampere´'s law with the correction term I have a infinite cylinder with radius R with a current density , and magnetic field . I have to proof that it is acceptable to discard the correction term of term of ampere's law, while calculating the magnetic field, as long as it obeys the following...- anaisabel
- Thread
- Replies: 8
- Forum: Advanced Physics Homework Help
-
K
E&M: Field of a Wire with non-uniform current
Summary:: Not sure if my solution to a magnetostatics problem is correct [Mentor Note -- thread moved from the technical forums, so no Homework Template is shown] I was trying to solve problem 2 from...- KDPhysics
- Thread
- Replies: 9
- Forum: Introductory Physics Homework Help
-
T
A Evaluating Matrix Spin Dependent Term in Dirac Quadratic Equation
I derive the quadratic form of Dirac equation as follows $$\lbrace[i\not \partial-e\not A]^2-m^2\rbrace\psi=\lbrace\left( i\partial-e A\right)^2 + \frac{1}{2i} \sigma^{\mu\nu}F_{\mu \nu}-m^2\rbrace\psi=0$$ And I need to find the form of the spin dependent term to get the final expression $$g...- thetafilippo
- Thread
- Replies: 1
- Forum: Quantum Physics